Table of Contents
2.1.Statements of Aims, Objectives, and Motivation
2.3.Advantages of Hexapod over Wheeled Vehicles
2.4.Disadvantages of Hexapod over Wheeled Vehicles
3.Fundamentals of Hexapod Robot
3.1.1.Swing and Stance phases of a Hexapod
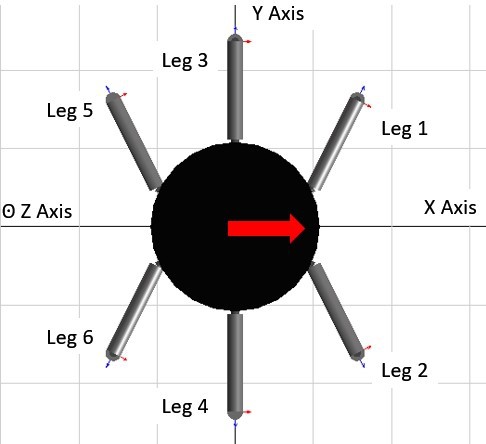
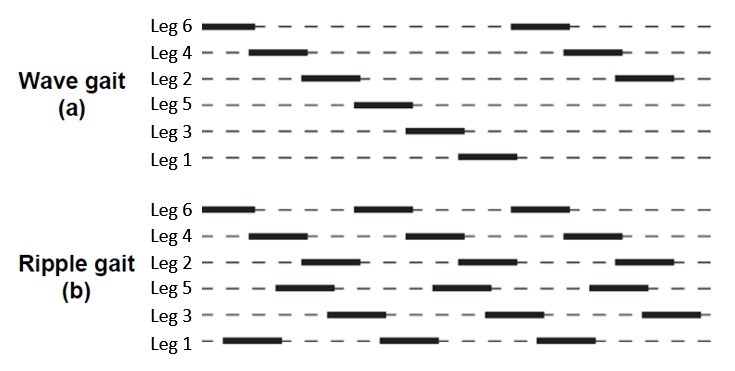
3.1.2.Tripod Gait, Wave Gait, Ripple Gait
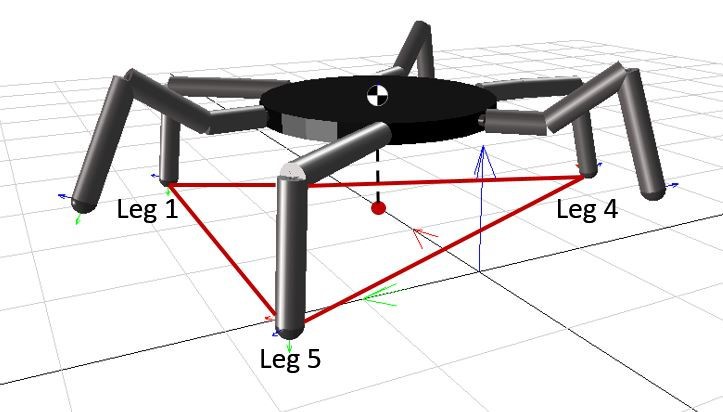
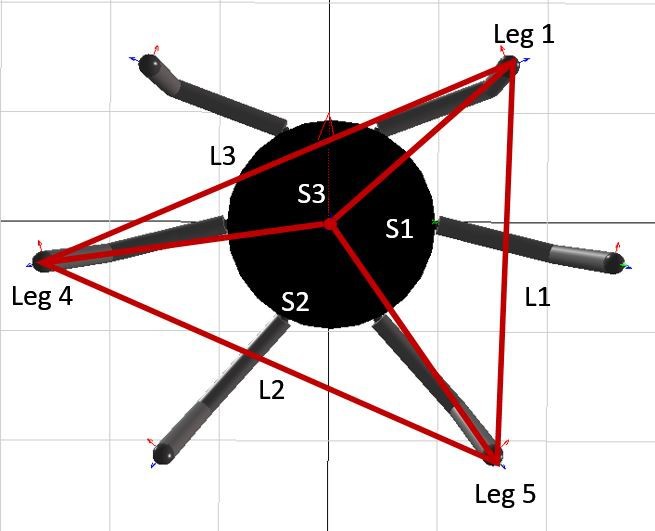
3.2.Stability of Hexapod Robots
3.3.Kinematics of Hexapod Robot
3.4.1.Dynamic Model of the Leg Mechanism
4.Hierarchical Control Architecture
4.3.2.Stability Detection and Recovery
8.Appendix
8.1.Additional Visuals
8.2.Additional Equations
8.3.MATLAB Code

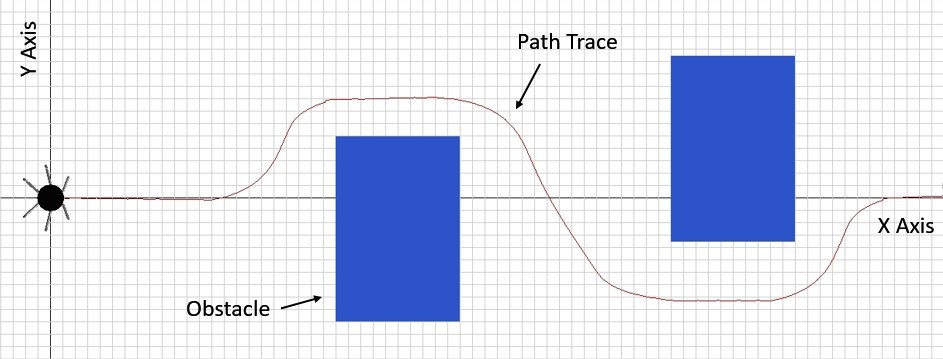
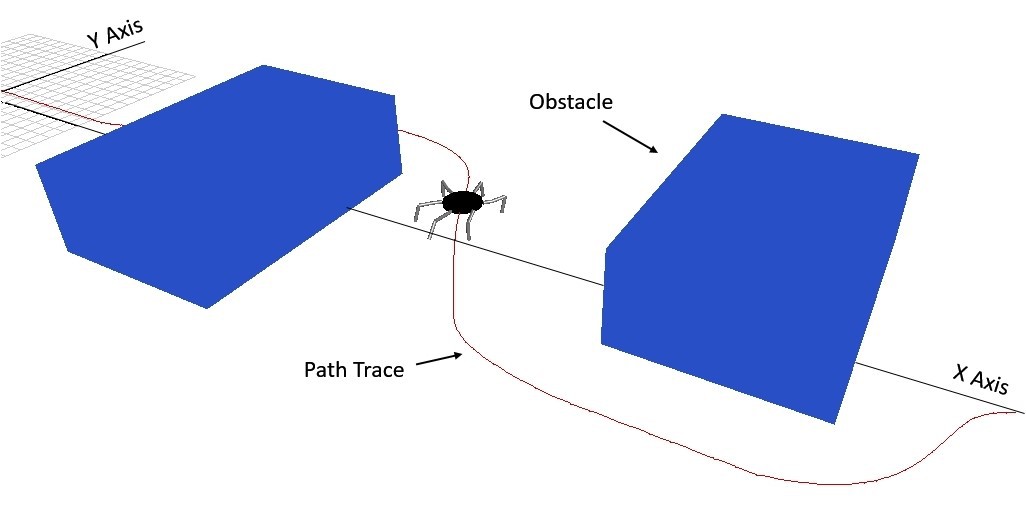
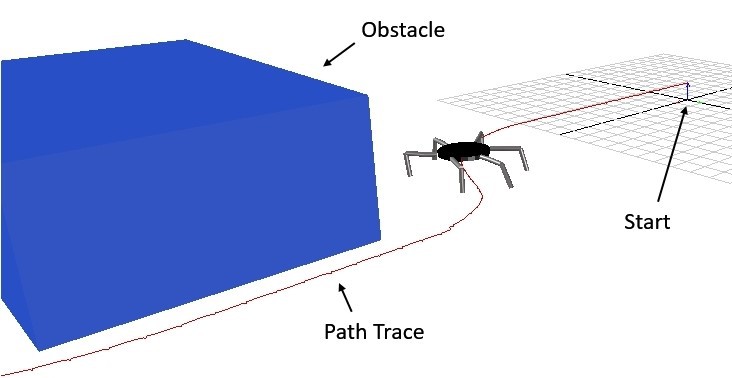

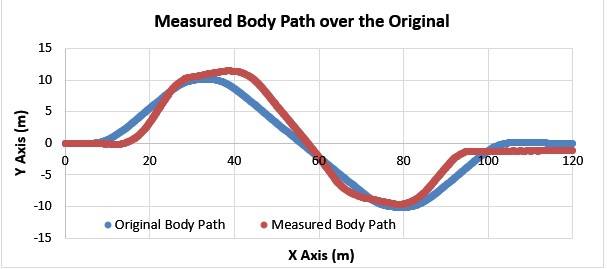
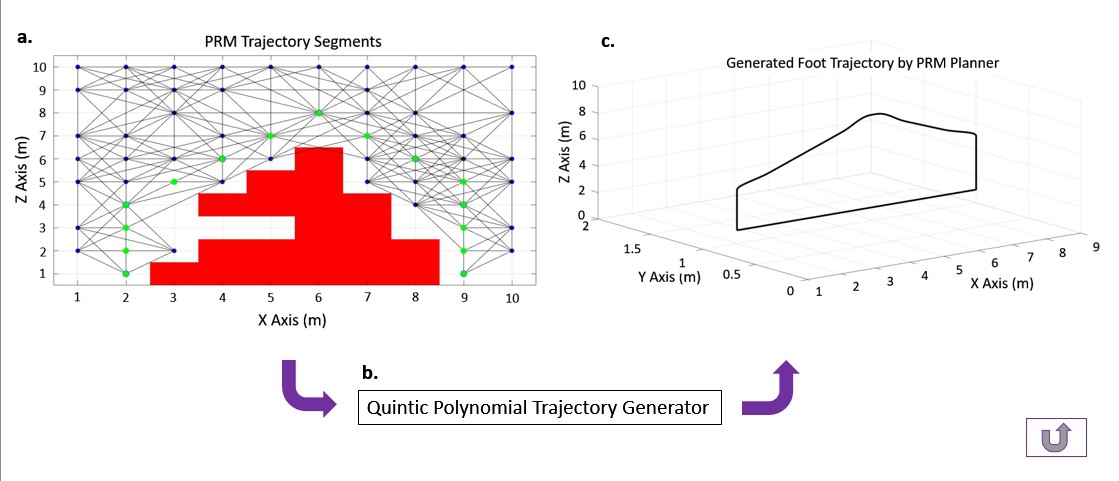
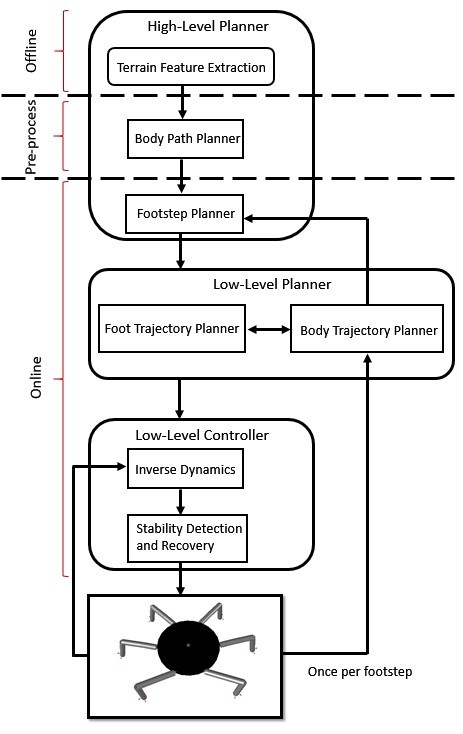
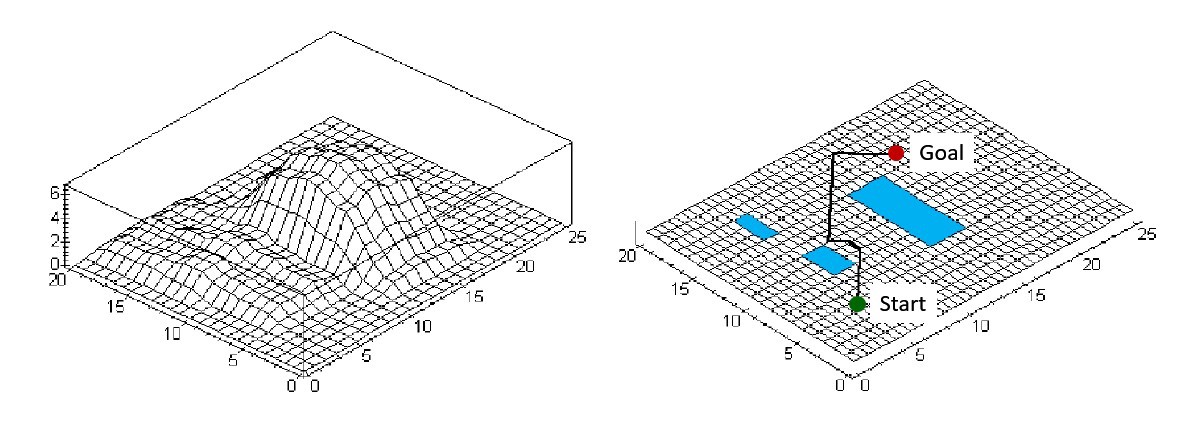 Figure 4.2-a Uneven terrain and the 2D representation of terrain, adapted from [15]
Figure 4.2-a Uneven terrain and the 2D representation of terrain, adapted from [15]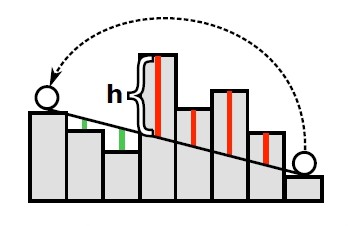 Figure 4.3 Collision map of a foot trajectory over an obstacle, adapted from [28]
Figure 4.3 Collision map of a foot trajectory over an obstacle, adapted from [28] 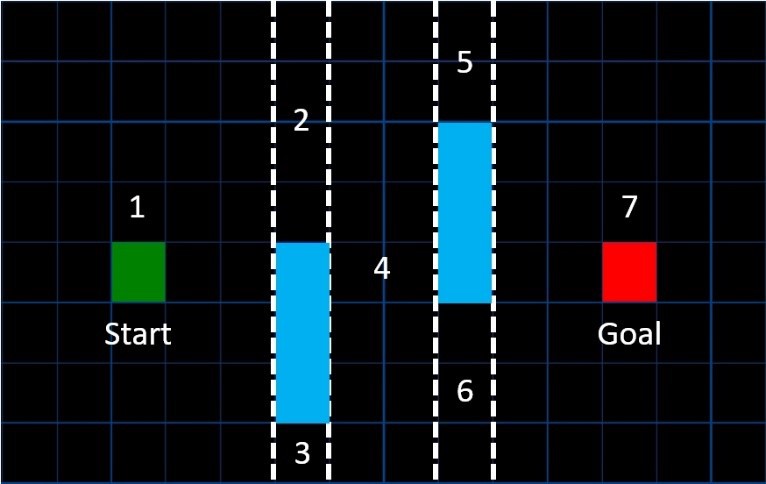 Figure 4.4 Occupancy Grid Representation
Figure 4.4 Occupancy Grid Representation Figure 4.5 Adjacency Map of the Occupancy Grid.
Figure 4.5 Adjacency Map of the Occupancy Grid. A* (star) path planning algorithm determines the cost of the 8 surrounding nodes by using Equation 28,
A* (star) path planning algorithm determines the cost of the 8 surrounding nodes by using Equation 28,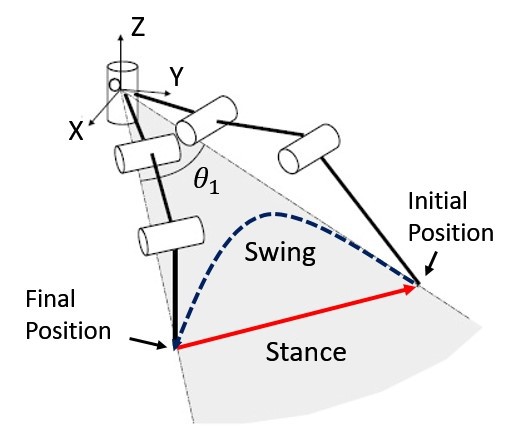




 Cirmall
Cirmall
 Vinícius Jean Ferreira
Vinícius Jean Ferreira
 ensafatef
ensafatef
 ssla-couk
ssla-couk
This is great! Are you planning on posting the source code for this project?