In this chapter, the fundamental concepts of hexapod robots such as walking gaits, stability, kinematics and dynamics are covered which are essential to obtain a better understanding of the control architecture that is delivered in the next chapter.
3.1.Walking Gaits
In this section, the phases in a leg cycle are introduced, then different gaits are covered and simulations results are represented.
3.1.1.Swing and Stance phases of a Hexapod
Figure 3.1 shows the swing and stance phases of a robot leg cycle. A leg cycle is the combination of raising and placing a leg and it consists of 2 stages: the swing phase and the stance phase. During the swing phase, the leg traverses from the initial position to final position through air, shown by blue dashed line. On the other hand, during the stance phase, the leg end effector is in ground contact while the leg traverses from the final position to the initial position, moving the robot in the opposite direction to the red arrow.
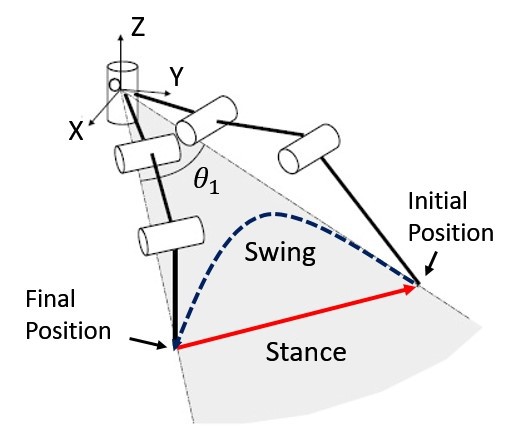
Figure 3.1 Robot leg cycle divided into swing and stance phases, adapted from [20]
3.1.2.Tripod Gait, Wave Gait, and Ripple Gait
There are 3 walking gaits that are commonly observed in the nature: wave gait, ripple gait, and tripod gait. The tripod gait was covered in the progress report which is provided in the Appendix 8.3. Wave gait is the slowest in terms of the locomotion speed, yet the most stable. In the wave gait, only 1 leg is in the swing phase at a time while the other 5 legs are in the stance phase. The locomotion speed of ripple gait is slower than tripod gait nevertheless it is faster than the wave gait, since 2 legs from opposite sides are in the swing phase by 180 degrees offset, at a time. These 2 walking gaits are shown in Figure 3.3 where the solid lines and dashed lines represent the swing phase and stance phase, respectively [17]. Figure 3.2 shows the numbering of the hexapod robot legs where the red arrow specifies the front of the robot that was created in the MapleSim environment.
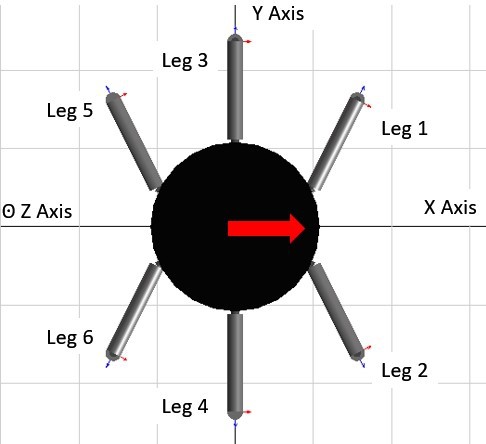
Figure 3.2: Top view of the robot model that was used in the simulations
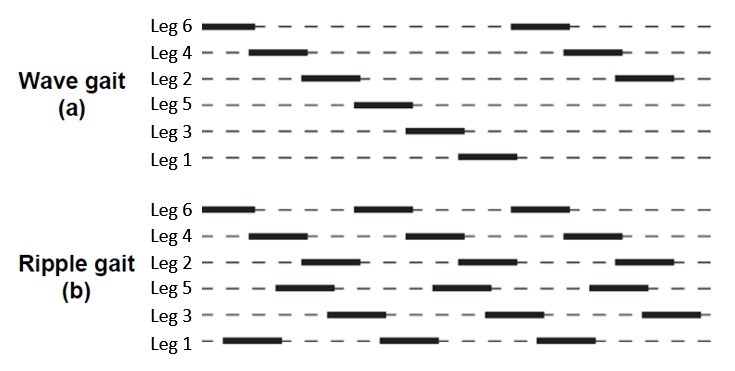
Figure 3.3 Sequence of swing and stance phases in walking gaits, taken from [17]
3.2. Stability in Hexapod Robots
The stability of legged robots is divided into two categories: static stability and dynamic stability. To be considered statically stable, the robot needs to be stable during its entire gait cycle, without the requirement of any force to balance the robot [20]. While the robot is statically stable, the vertical projection of its centre of mass (COM) is located within the support polygon which is formed between the legs that are in the stance phase. In the case of COM being positioned on the border or outside the support polygon, the robot falls over unless it is dynamically stable, i.e. robot is balanced while walking due to the inertia caused by the motion and is statically unstable when it stops moving [21]. Figure 3.4 demonstrates the support polygon of the MapleSim model during tripod gait where the red circle denotes the vertical projection of its COM.
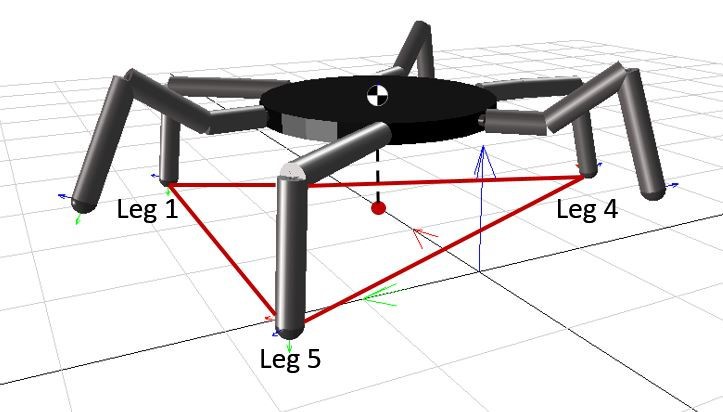
Figure 3.4 The Support Polygon that is formed During Tripod Gait.
Figure 3.5 shows the bottom view of the hexapod robot where the support polygon is decomposed into 3 sub-triangles in order to calculate the Stability Margin.
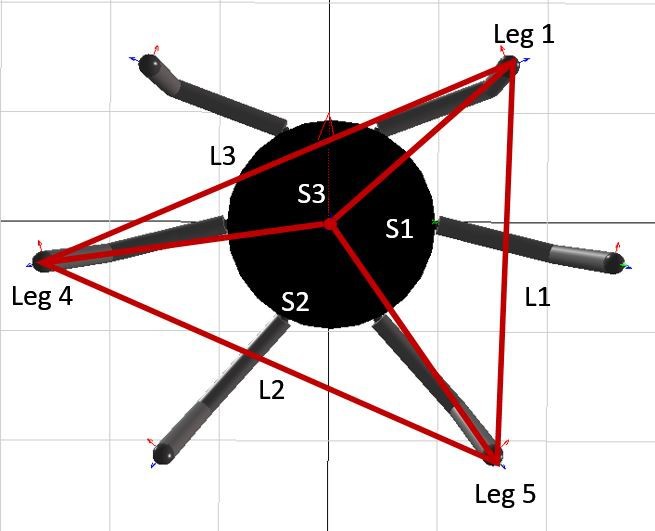
Figure 3.5 The Bottom View of the Support Polygon Decomposed into Sub-triangles.
Following [22], the area of the convex pattern between Leg 1, Leg 5 and the projection of COM is calculated by Equation 1.
S1= 1/2 |(X1-Xc)*(Y5-Yc)-(X5-Xc)*(Y1-Yc)| (1)
The distance between two ground contact points of Legs 1 and 5, is calculated by Equation 2.|L1|=√((X5-X1)^2+(Y5-Y1)^2 ) (2)
h1=(2*S1)/|L1| (3)
Since the area of a triangle is the product of base and height divided by two, the perpendicular distance,, from the vertical projection of COM to L1 is given by Equation 3. Figure 3.6 shows the heights of the 3 sub-triangles.
Figure 3.6 Heigths of the sub-triangles
Then, the same process is repeated to calculate S2, h2, S3 and h3. Stability margin (SM) is the shortest distance between the position of COM projection and the support polygon borders [20]. In this particular example, SM is equal to . The mathematical expression for SM is given by Equation 4.
SM=min(h1,h2,h3) (4)
The state of variable indicates whether or not the robot is statically stable. The mathematical expression for is given by Equation 5,T=1 if Sk=A (5)
T=0 if Sk≠A (6)
where n is the number of legs in stance position at a given time and A is the area of the entire support polygon. Figure 3.7 shows the variations in SM while the robot follows the body path that is used in the experiments shown in red. The MapleSim code that was used to calculate the SM, is shown in Figure 8.2 (in Appendix).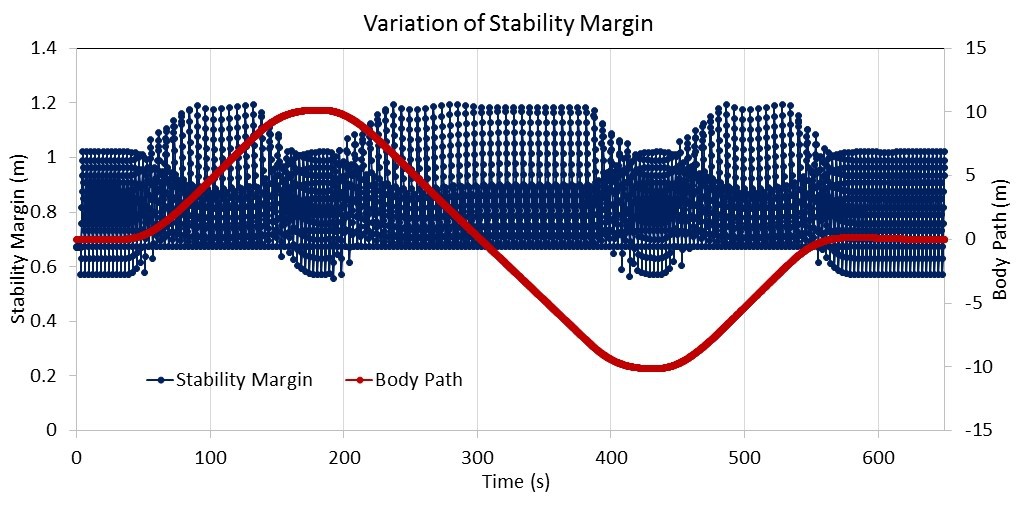
Figure 3.7 Variation in the SM while the robot is following the given body path
The variable was used in the simulation to terminate the process if the robot becomes statically unstable. Although, this is not a concern in the level terrain, when the robot navigates on an incline surface as it is demonstrated in Figure 3.8, the vertical projection of the COM is closer to the borders of the support polygon, making the robot more likely to be statically unstable. There are two ways to solve this problem. The first one is to implement an adaptive gait generation and the second one is to make the robot dynamically stable. These two proposed solutions are tested in the MapleSim environment and the findings are presented in Section 4.2.2.
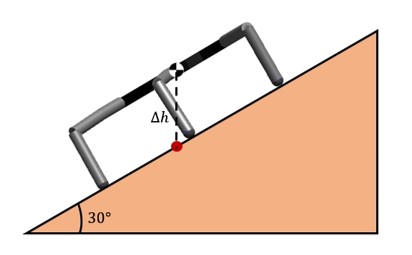
Figure 3.8: Side view of the hexapod model on an incline surface of
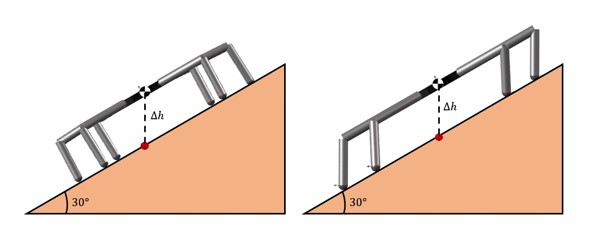
Figure 3.9: Front view of the hexapod model on an incline surface of
Figure 3.9 shows how θ3 of Joint 3 is altered to ensure that Link 3 is perpendicular to the horizon, this is achieved by an geometric approach where the roll angle of the body was measured by an Euler Sensor. Then, the output from the sensor, γ was added to or subtracted from θ3 that was calculated by the inverse kinematic equations, depending on the direction of the robot. The block diagram of the procedure is shown in Figure 3.10. An analytical approach can be found in [23].
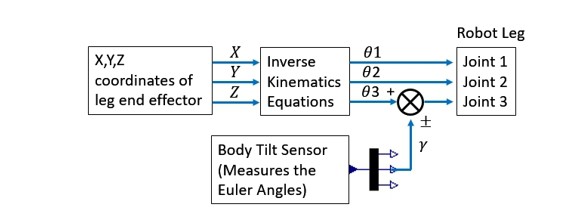
Figure 3.10: Posture Control – Block Diagram.
3.3.Kinematics of Hexapod Robot
3.3.1.Forward Kinematics
The forward kinematics is used to derive a set of kinematic equations that yields the position and the orientation of the robot end effector for the given joint parameters of the robot manipulator [16]. The derived equations were used by the footstep planner to compute the workspace of the robot leg and to project potential final configurations for the robot end effector. Denavit-Hartenberg (DH) convention states that each homogeneous transformation, Hi, can be expressed as a product of 4 transformations, given by Equation 6,
Hi=R(Zi,θi) T(Zi,di) T(Xi,ai) R(Xi,αi) (6)
where R and T denote rotation and translation, respectively [16]. Equation 7 shows the matrix that has been calculated from the product of 4 transformation matrices given in Equation 6.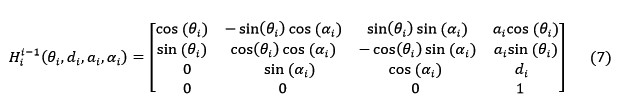

given by Equation 9 [24].
Figure 3.11 demonstrates the leg of simulation model that was developed in the MapleSim environment and Figure 3.12 shows the corresponding diagram that was used to obtain the DH Parameters.
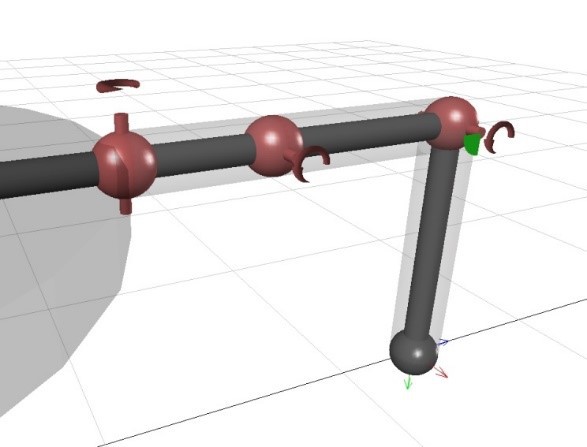
Figure 3.11: Simulation Model Leg
The DH Parameters of each leg is given by Table 2-1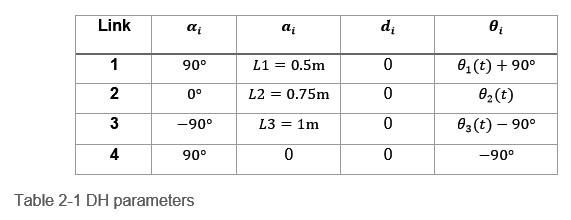 Table 2‑1 DH parameters
Table 2‑1 DH parameters 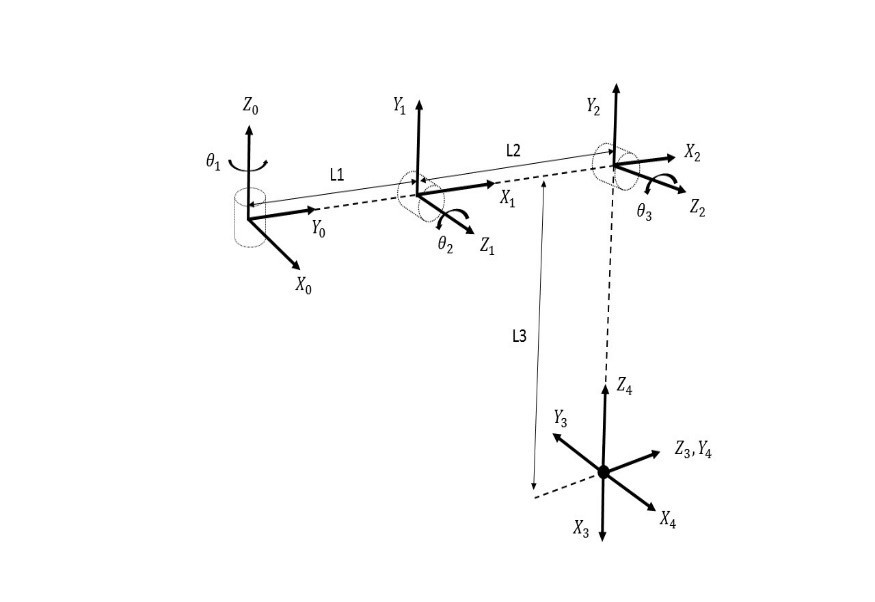 Figure 3.12 Forward kinematic model of the robot leg
Figure 3.12 Forward kinematic model of the robot leg
In order to verify the obtained DH Parameters, MATLAB Script 8-1 (in Appendix) was used to calculate the end effector coordinates of the robot leg when it is in the rest position, i.e. θ1, θ2, and θ3 are equal to 0 degrees. Equation 10 shows the calculated Cartesian coordinates, using MATLAB Script 8-1, which are the same as the coordinates of the end effector, shown in Figure 3.13 confirming the DH Parameters to be correct.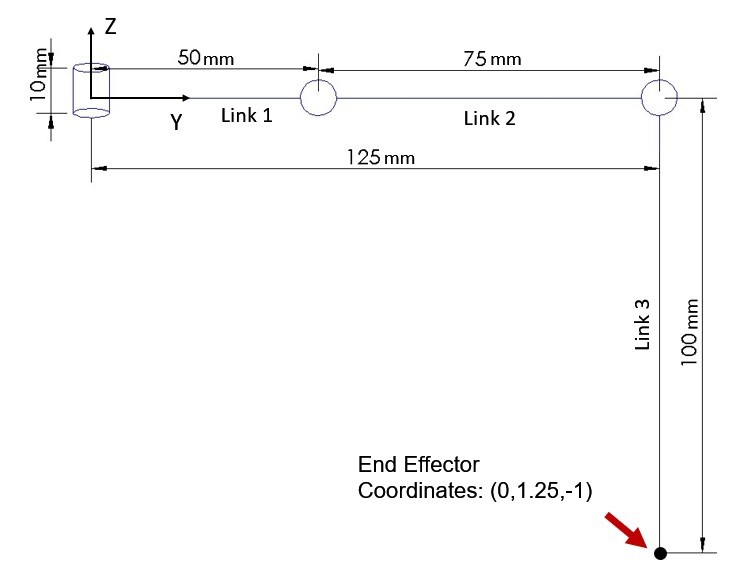 Figure 3.13 Hexapod leg in rest position
Figure 3.13 Hexapod leg in rest position
The DH Parameters that are shown in Table 2-1 are used to visualise the reachable workspace of the robot leg. Figure 3.14 illustrates the 3D view of the end effector positions and Figure 3.15 illustrates the side views where; θ1 was altered from -90 to 90 in increments of 10 degrees, θ2 was altered from -90 to 90 in increments of 15 degrees, and θ3 was altered from -60 to 135 in increments of 15 degrees. MATLAB Script 8-2 that is provided in the Appendix, was used to generate Figures 3.14 and 3.15.
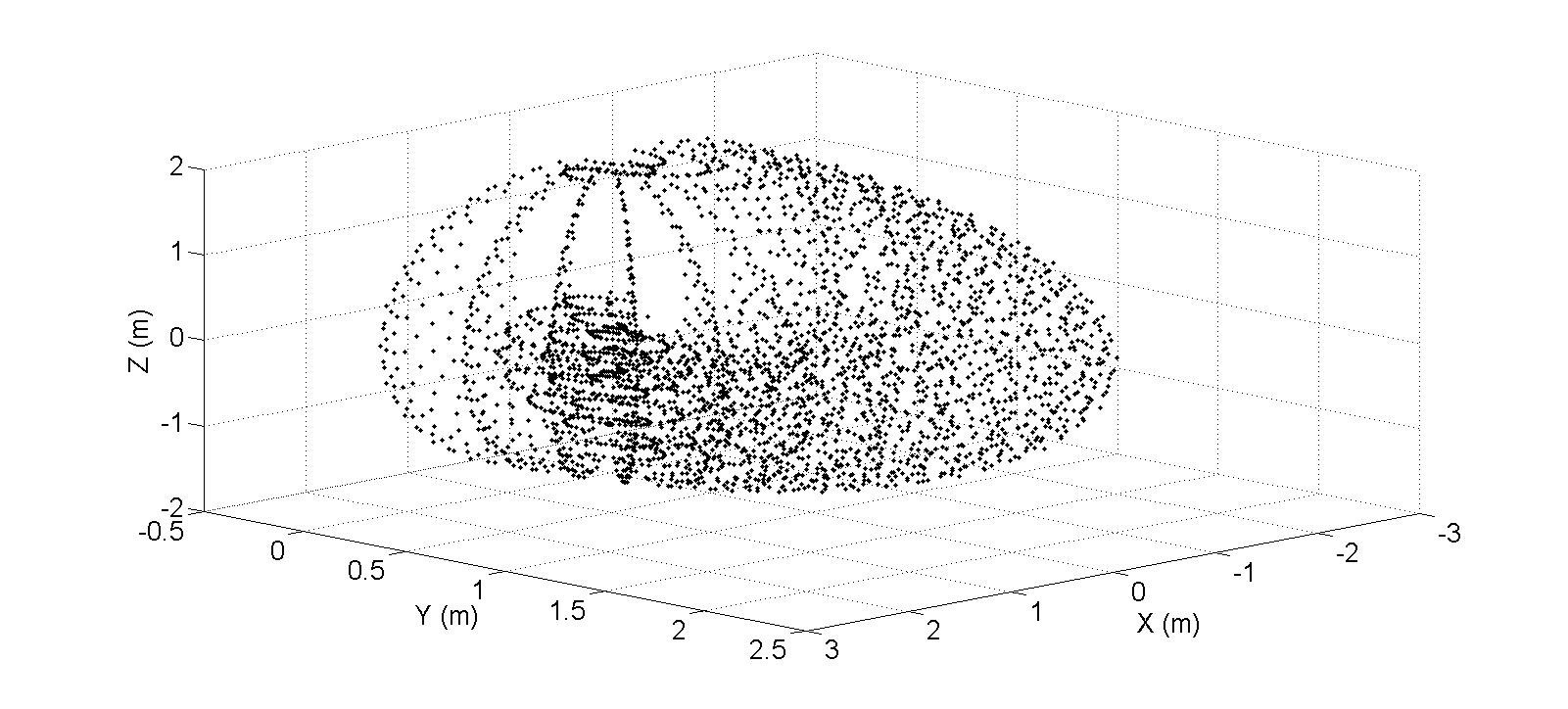 Figure 3.14 3D view of the reachable workspace of robot leg
Figure 3.14 3D view of the reachable workspace of robot leg
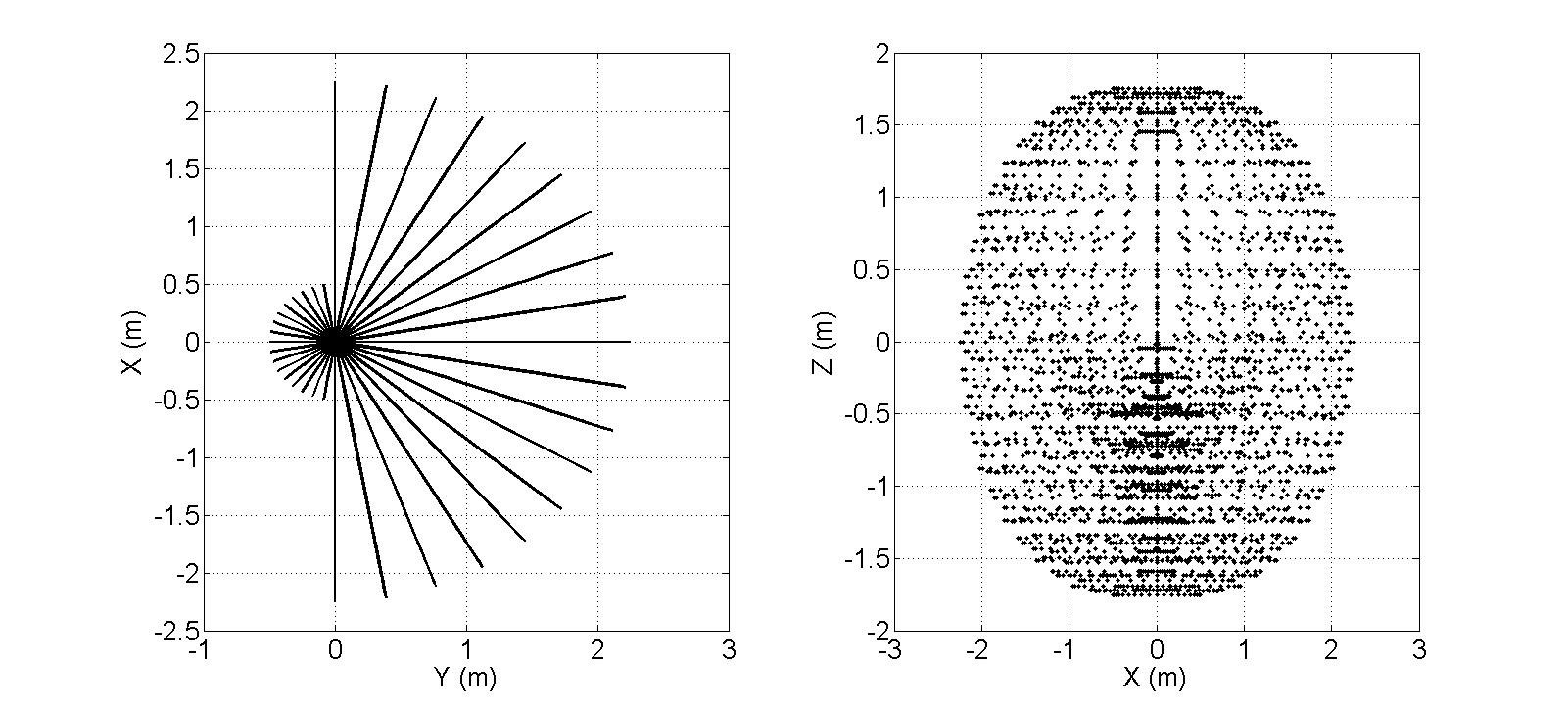 Figure 3.15 X-Y and Z-X views of the reachable workspace of robot leg
Figure 3.15 X-Y and Z-X views of the reachable workspace of robot leg
The same approach can be applied to calculate the combinations of revolute joint angles, θ1, θ2 and θ3 that cause a collision with an obstacle that is located within the workspace of the robot leg. Figure 3.17 demonstrates the angles combinations that the leg end effector collides with the obstacle shown in Figure 3.16.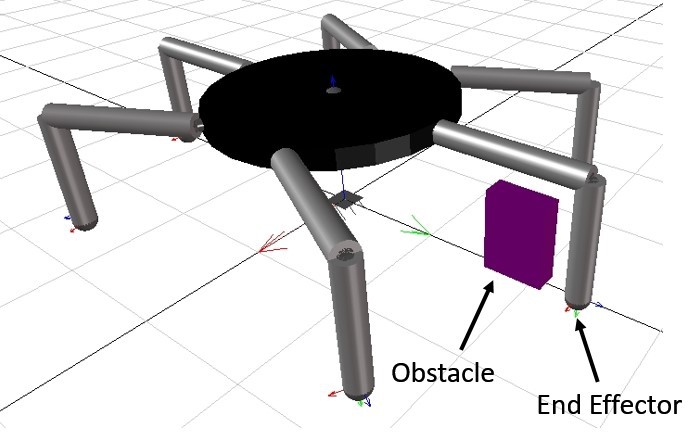 Figure 3.16 MapleSim Model and Obstacle located within the Workspace of Leg 3.
Figure 3.16 MapleSim Model and Obstacle located within the Workspace of Leg 3.
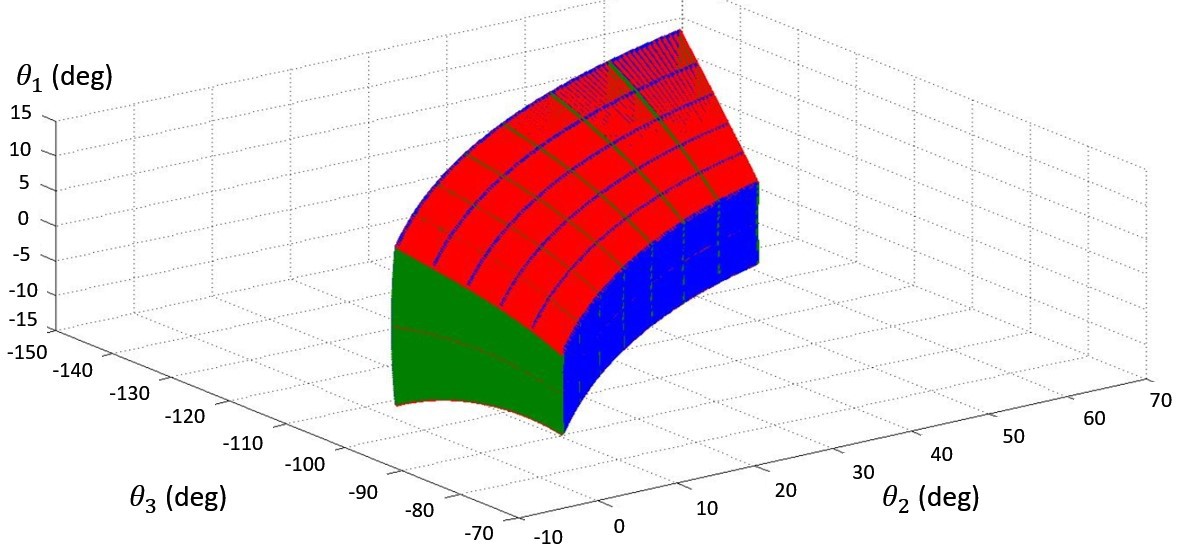 Figure 3.17 The combination of angles that cause a collision with the Obstacle.
Figure 3.17 The combination of angles that cause a collision with the Obstacle.
3.3.2.Inverse Kinematics
As the complexity of the system increases, the robot is desired to
undertake as many calculations as possible since the computation capabilities
of human operator is limited. [12]
Similarly, calculating the angle of joint rotation for 6 legs in order to move
the hexapod robot from position A to position B is a challenging task for the
operator therefore, the robot is required to compute this calculation and be capable
of moving the end effector of the robot legs to the given coordinates. This
task is handled by inverse kinematics equations in which the joint angles are
calculated that will make the end effector achieve the particular X, Y, and Z
coordinates. [39]
The derivation of equations are as follows:
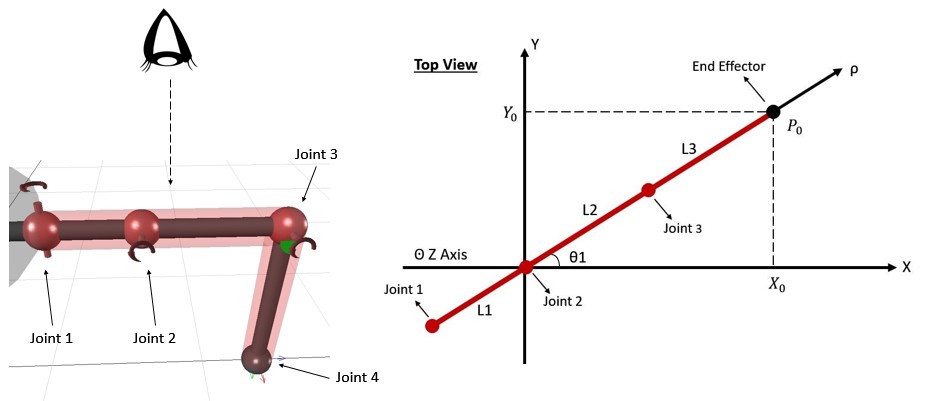
Figure 3.3.1 Top view of a single robot leg
Figure 3.3.1 shows the top view of a single robot leg. An axis is defined in the direction of the leg and it is labelled as ρ. The coordinates of the end effector are (Xo,Yo) and the angle of rotation about the Z axis is θ1.
The origin has been defined as the centre of the Joint 2 since the θ1 is independent of where the origin of the leg is defined due to Z rule in geometry. In other words, defining the Joint 1 as the origin of the robot leg would simply add an offset of L1 to the system. The θ1 is calculated by Equation 1:
The distance between the origin and the end effector is expressed as:
Figure 3.3.2 and 3.3.3 demonstrate the side view of a single leg.
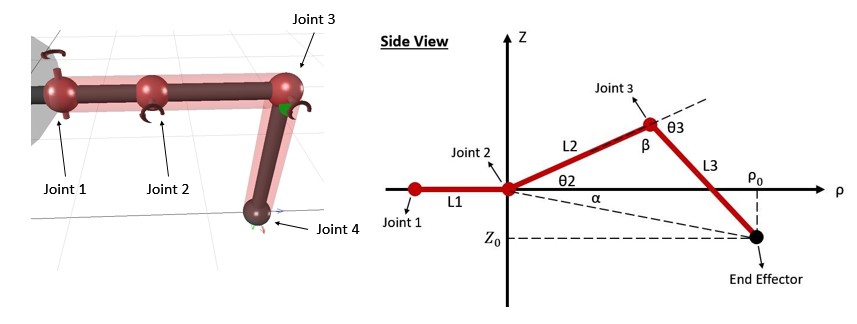
The coordinates of the end effector are (ρo,Zo). The distance between the origin and the end effector is
The angle between L2 and L3 is labelled as β and it is computed by applying law of cosine.
Equation 5 demonstrates the expression for the angle α.
The θ2 is calculated by applying the law of cosine which indicates that

3.4.Dynamics of Hexapod Robot
The robot dynamics provides the relationships between the robot motion, i.e. acceleration and trajectory, and the forces that are involved within the motion such as actuation and ground contact forces [3] [25]. A robot leg can be treated as a 3 DOF manipulator where the ground contact is the end effector and hence the dynamic model of a robot leg is obtained by examining the dynamics of leg mechanism [3].
3.4.1.Dynamic Model of the Leg Mechanism
The dynamic model of the leg mechanism yields a set of differential equations, i.e. equation of motion which is derived by using the Lagrangian approach [25]. The Lagrange-Euler formulation provides a relationship between the motion of the leg and the joint actuator forces [25]. Alternatively, Newton-Euler formulation may be used which, unlike Largangain formulation, requires to compute the accelerations in all and axis and to solve for the constraint forces [26]. The Lagrange-Euler formulation has been chosen over standard Newton formulation for deriving the dynamic equations of motion since it avoids the computation of some constraints [3] [26] [24]. Figure 3.18 shows the Denavit-Hartenberg representation of a 3 DOF robot leg where the centre of gravities (COG) of Links 1, 2, and 3 are demonstrated.
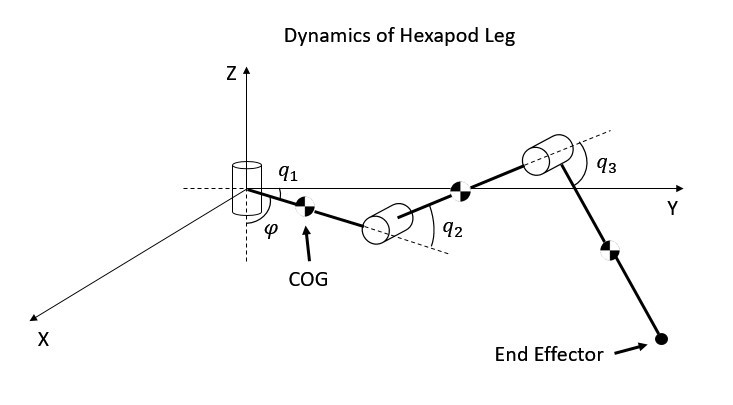
Figure 3.18 Dyanmic model of a robot leg
Since the revolute joint 1 rotates only about the Z axis, the angle φ, is equal to 0 regardless of the orientation of the leg. The coordinates of each COG are calculated as given by Equations 11-19.
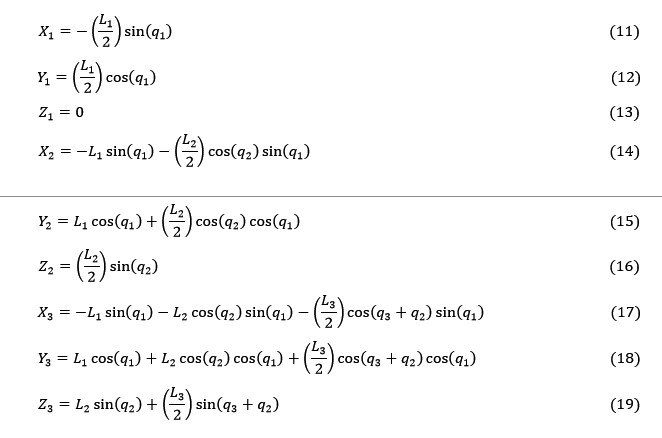
 Figure 3.19 Caartesian coordinates of COG of links 1, 2, and 3
Figure 3.19 Caartesian coordinates of COG of links 1, 2, and 3
Equation 20 shows the dynamic expression of the robot leg in matrix form,



3.4.2.Contact Force Estimation
Figure 3.20 shows the reaction forces, R1, R4, and R5 that apply to the ground contact points, in tripod gait when legs 1, 4, and 5 are in the stance phase. The red triangle that is formed between the contact points is the support polygon of the robot. Note that, in Figure 3.20, the legs that are in the swing phase are not displayed. The diagram in Figure 3.21 shows the ground contact force, R1 when Leg 1 is in the stance position, and the other 3 forces that are associated with the COG of each link.
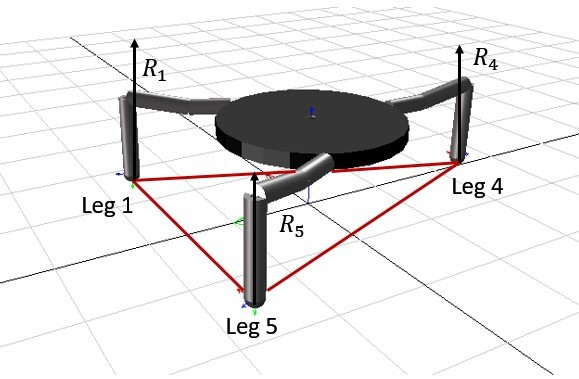
Figure 3.20 Reaction forces during tripod gait - legs 2, 3, and 6 are not shown
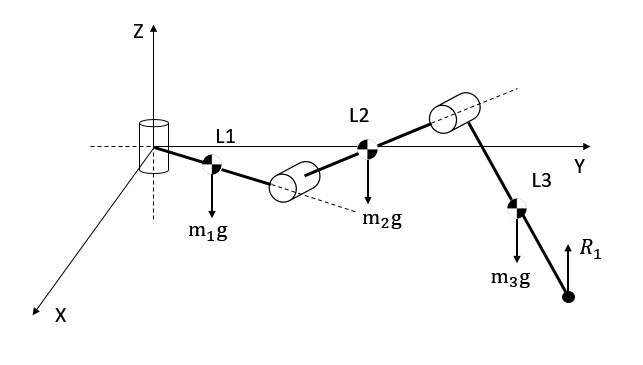
The ground contact forces in the Z direction are calculated by Equation 27,

Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Excellent article! Thank you!
Are you sure? yes | no
Very nice article, some latex formulas arent't visible yet. Can you give me the material or fix the problem please? Thanks
Are you sure? yes | no
Hey nice project here, I see in your calculations on the support polygons, and I can't figure out what is Xc and Yc when youre calculating S1, could you please tell what this represents?
Are you sure? yes | no
Xc,Yc, etc would be the XYZ of the "center" point or CoG....to be a bit more precise it's the center-of-pressure which is the CoG projected down onto the ground (CoP). In his formula any two legs and CoP form a triangle. In tripod gate, you would have 3 of these triangles, you calculate the height (h) of each of these three triangles and then take the smallest (h) as the support margin. If the robot is moving, then over time this (h) is going to zero and you'd need a swing leg to land to maintain support. (h) has a velocity vector so you can use this to determine when in future it will hit 0 and you must land a leg within that time.
Are you sure? yes | no