1. BACKGROUND
Cosmic rays are particles and nuclei which bombard the earth from all directions [1]. The Greisen-Zatsepin-Kuzmin (GZK) limit is a theoretical upper limit on the energy of cosmic rays from distant sources of 5*10^19 eV. The limit is set by their propagation to us through the cosmic microwave background radiation (CMBR) [4]. However, cosmic ray energies have been experimentally determined to vary from 10^8 eV to well beyond 10^20 eV. The identification of sources of ultrahigh-energy cosmic rays (UHECR), cosmic rays from distant sources with energies above the GZK limit, has been a great challenge since they were first observed in 1962 [1]. The observed existence of these particles is the GZK paradox: Why is it that some cosmic rays appear to possess energies that are theoretically too high, given that there are no possible near-Earth sources, and that rays from distant sources should have scattered off the cosmic microwave background radiation?
Detecting the cosmic rays themselves is difficult; only a handful have been directly detected in the last 50 years. The only way to detect UHECR is through their interaction with the earths atmosphere, producing a cascade of billions of particles that excite nitrogen molecules in the air and spread out over a large area once they reach the ground [1]. When a primary cosmic ray produces many secondary particles, this is called an air shower. When many thousand, millions, even billions of particles arrive at ground level this is called an extensive air shower (EAS). When cosmic rays interact with nuclei in the air, pi-mesons (pions) are created. Neutral pions decay very quickly, usually into two gamma rays. The gamma rays from the neutral pions may also create new particles, an electron and a positron, by the pair creation process, and these electrons and positrons may produce more gamma rays by the bremsstrahlung mechanism. Charged pions decay into a muon and neutrino but after a longer time than neutral pions, so some charged pions may collide with more nuclei in the air to produce even more new particles [2].
These air showers form cones of particles, meaning detectors on the ground can determine the place in the atmosphere where the original cosmic ray hit. Dozens of such cosmic ray observatories exist. In 2007, the Pierre Auger Observatory, consisting of 1600 detectors spaced 1.5km apart, found a strong association between cosmic ray direction and nearby active galactic nuclei, galaxies hosting central black holes which may eject plasma jets into intergalactic space [1]. However, more observatory data are necessary to properly understand cosmic rays and solve the GZK paradox.
2. DESIGN
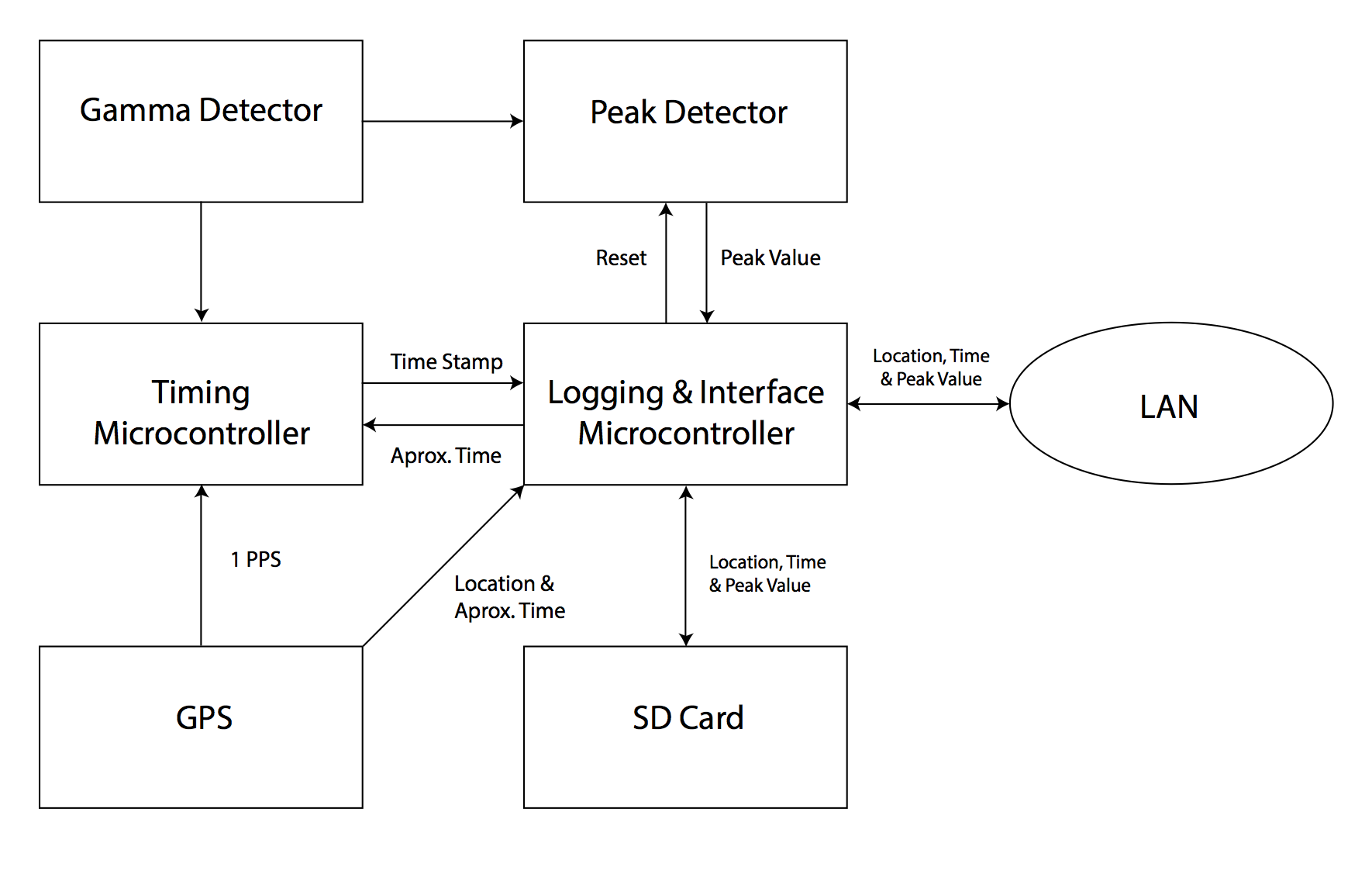
Figure 1: Flow of information within each observatory node
The cosmic ray observatory is comprised of many individual detector nodes. When struck by a single gamma ray photon, a node must be able to record the time the photon struck to within a few nanoseconds, the energy of the photon, and the location of the node. It must then be able to store this data and later send it to a master database. Each node contains two microcontrollers: a timing microcontroller dedicated to precisely measuring the time the photon strikes, and a logging and interface microcontroller to measure photon energy, record data to an SD card, and communicate with the master server. Both can be atmel atmega microcontrollers, and the logging and interface microcontroller can be a raspberry pi. However, the timing microcontroller cannot be a raspberry pi because even with a real-time linux kernel, latency is inconsistent and unacceptably high at around 28 microseconds [3].
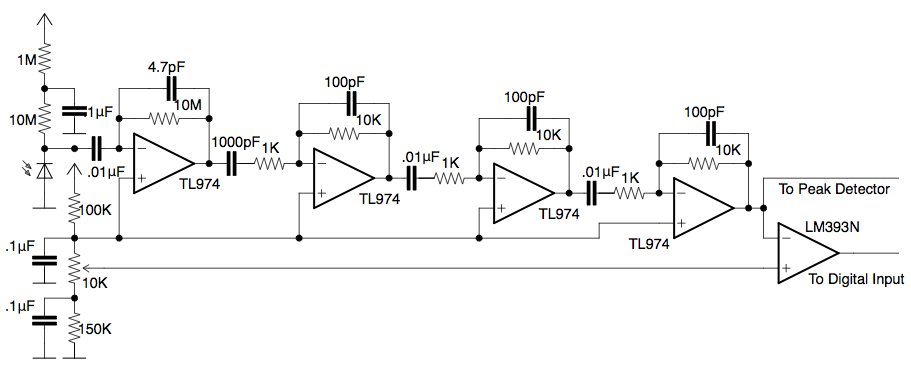
Figure 2: PIN diode gamma ray photo detector. Current generated when a photon strikes the PIN diode is amplified through four op amps; a comparator then sends a pulse when the signal dips below a threshold.
The heart of a node is its PIN diode detector (figure 2), based on a 2003 Maxim application note, which uses a photodiode with a large lightly-doped intrinsic region very sensitive to electromagnetic radiation [5]. It is very important that this section be properly shielded from stray electromagnetic radiation and visible light. When a photon hits the diode, a small current is produced proportional to the energy of the photon [6]. A large series resistance turns this current into a small voltage, which is then amplified with op amps. Capacitors are placed in parallel with feedback resistors to prevent oscillation. The waveform amplified has critical frequencies at 10kHz to 200kHz, meaning amplifier bandwidth, the point at which the amplified signal decreases by 3dB, must be large enough to not distort the signal, so four op amps are cascaded in order to increase bandwidth. An op amp has a specific gain bandwidth product (GBWP), so as gain increase, bandwidth decreases. By cascading op amps and decreasing the gain of each, bandwidth is increased dramatically as the reduction in bandwidth from cascading is far less than that of increased gain.
After the signal is amplified, a comparator detects that the signal has dropped below a threshold and sends a pulse to the timing microcontroller in order to record the time when the photon struck. The amplified signal is also sent to a peak detector circuit (figure 3) so that photon energy can be determined. The diode prevents current from flowing out of the capacitor, meaning that the voltage across it is always the maximum value of the waveform. A transistor is used to discharge the capacitor so that the peak value of the next photon can be determined. One problem with the peak detector circuit is that reverse leakage on the diode might be large enough to significantly discharge the capacitor. To mitigate this, a second diode and voltage feedback can be added, making the voltage across the diode zero and nearly eliminate all reverse leakage. (figure 4)
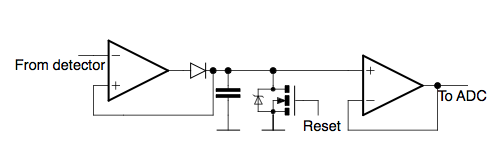
Figure 3: Peak detector circuit.
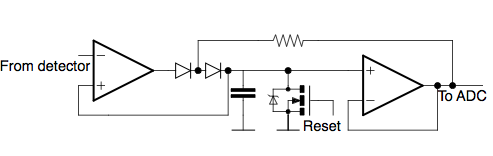
Figure 4: Alternative peak detector circuit with the advantage of greatly reducing reverse leakage.
A GPS module is used to accurately determine location and time. The module connects with serial to the logging and interface microcontroller to give location and approximate time. This approximate time is sent to the timing microcontroller, which uses it in conjunction with the highly-accurate one pulse per second (1PPS) output of the GPS module and its own crystal oscillator-based clock to know the time to within a few nanoseconds. The timing microcontroller counts the number of timer ticks between 1PPS pulses to determine the exact speed of the timer. This means the crystal oscillator does not need to be very accurate or have a low thermal coefficient, as the 1PPS signal will automatically compensate. When the timing microcontroller receives a pulse from the gamma ray detector, it sends the exact time stamp to the logging and interface microcontroller.
Once the logging and interface microcon-troller receives the time stamp, it immediately reads the voltage of the peak detector, then resets it. The microcontroller then writes the location, time, and peak value to an SD card. Once enough data are gathered, the logging and interface microcontroller sends them to a server for storage on a master database. Communication between server and node can be accomplished through copper Ethernet, WiFi, or through a wireless mesh network of other nodes.
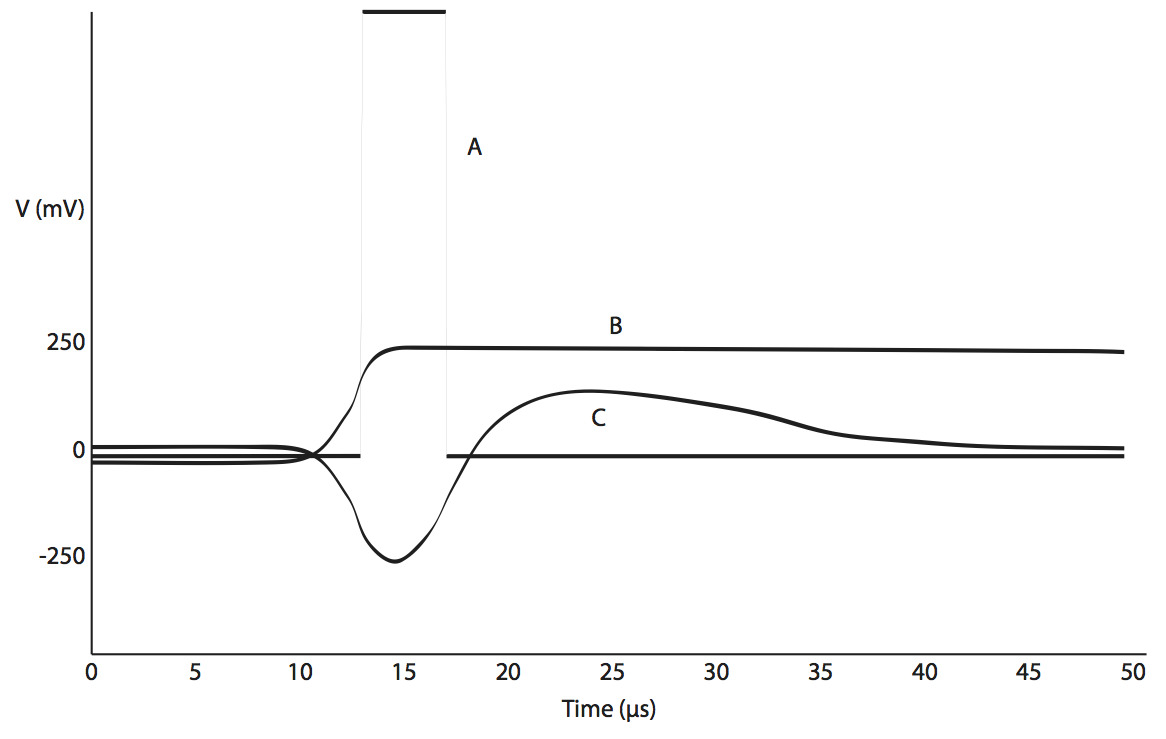
Figure 5: A. Comparator output B. Peak detector output C. Pre-comparator output
Parts for a single node cost only $50 to $150. This is dramatically less cost per node than any other cosmic ray observatory.
3. DATA ANALYSIS
Once data is collected from nodes to a master database, multilateration is used to find the apex of the air shower cone. Time difference of arrival (TDOA) among four nodes is necessary to form three hyperboloids, the minimum number to find a single point in space.
Theoretically, the intersection of these hyperboloids is where the cosmic ray struck. In reality, the hyperboloids will not intersect, and the most probable point must be found through optimization, such as with Newton’s method. Methods for multilateration are already very well established for use in GPS, and the same methods can be used to determine the apex of the cone. In addition to the location of the apex of the cone, the size can also be determined. This is done by simply counting the number of nodes affected by a certain air shower. The angle of the cone in relation to the earth can also be found by comparing the location of the apex to the location of the nodes affected.
4. Astronomy Applications
Because of the low cost and low power of each node, it is possible to create cosmic ray observatories of much larger scales at a far lower cost. In comparison, the Hundred Square-km Cosmic Origin Explorer (HiSCORE) has detectors which cost over $45,000 each [7]. These detectors are not only more expensive but also much larger. The advantage of a small, low-cost node is that it would be possible to span a cosmic ray observatory not over a hundred square kilometers but rather over a few hundred thousand square kilometers or more. Even home and schools around the world could be able to buy or make these nodes. This means one could theoretically make a cosmic ray observatory the size of an entire country. This type of observatory would be able to collect an unprecedented amount of data on cosmic rays and would undoubtedly aid in solving the Greisen- Zatsepin-Kuzmin paradox.
REFERENCES:
[1] J. Abraham and Gregory Snow. Correla-
tion of the highest-energy cosmic rays with
nearby extragalactic objects. Research Pa-
pers in Physics and Astronomy, 2007.
[2] Konrad Bernlhr. Cosmic-ray air showers, 1999.
[3] Emlid. Rasberry pi real-time kernal sd im- age, May 2014.
[4] R. U. Abbasi et al. Measurement of the flu of ultruhigh energy cosmic rays from monocular observations by the high resolution fly’s eye expirement. Physical Review Letters, 2007.
[5] Maxim Integrated. Gamma-photon radiation detector, September 2003.
[6] Burkhard Kainka. Measure gamma rays with a photodiode. Elektor, 2011.
[7] Simon Perks. Huge cosmic-ray observatory set for siberia, September 2012.
 aelias36
aelias36