For a bimolecular reaction
involving two molecules A and B, with concentrations [A] and [B] and a rate
constant K, the probability of the reaction occuring (from mass action) will
be K[A][B] . Assuming a time step which is short enough to make
the probability of reaction small during the step, the mass action probability
is equal to the probability ([A]>randA && [B]>randB && K>randK). Where && is
the logical and operation, and randA, randB and randK are
uniform-distribution random numbers (Salwinski and Eisenberg and Keane, et.al.).
We can therefore replace the expensive multiplies with inexpensive logical
operations and random number generation. Random numbers were generated using
a linear
feedback shift register technique. The shift register length was chosen
so that only one xor operation was needed.
The first reaction scheme I implemented is a slightly expanded version of the system presented in Salwinski and Eisenberg. Expansions were the ability of several update events to occur for a given molecular species (as in Keane, et.al.). Examples are below. Each chemical concentration is represented by a 16-bit integer. Each reaction path can increment (+1), decrement (-1), or not change the integer concentration of a chemical at each time step. The restriction of only simple increment/decreement means that reaction probabilities must be adjusted so that the likelyhood of changing the chemical concentration by two or more is negligible. In practice the probability of reaction is set to less than 0.01, so that the probability of two events occuring is less than 0.0001. Salwinski and Eisenberg limited the update so that only one reaction could update any chemical at any time step. I added a queue so that several reactions can update a chemical at each time step. The advantage of my scheme is simpler reaction control, the disadvantage is a longer state machine on each time step. Each time step is seven clock cycles, allowing six inc/dec inputs per chemical per time step.
 More
generally, what we are doing here is approximating a truncated Poisson
distribution of reaction events. We can make a better approximation by
allowing concentrations to change by more than +1/-1. Let's say that we
make the criterion that our approximation of the Poisson distribution
has to cover 99.99% of the full distribution. Or, put differently, the
cumulative sum of the discrete distribution has to be 0.9999 up to the
point we truncate. I wrote a matlab program
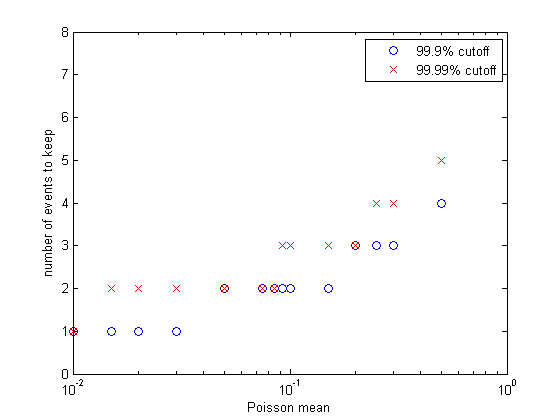
to plot the event number at which the cumulative probability reached
0.999 and 0.9999. The figure (left) shows the results. Keeping only one
event per reaction time step limits us to a mean rate of 0.01 at 99.99%
capture and about 0.03 at 99.9% event capture. For a mean reaction rate
up to about 0.085/time step, keeping up to two events per reaction
captures 99.99% of the events. Keeping three events allows reaction
rates up to about 0.2/time step (at 99.99% capture). So using the 99.99%
criterion, keeping two events instead of one event gives us about an
8-fold speed up, while keeping three events only gives us another factor
of two above the two-event rate.
More
generally, what we are doing here is approximating a truncated Poisson
distribution of reaction events. We can make a better approximation by
allowing concentrations to change by more than +1/-1. Let's say that we
make the criterion that our approximation of the Poisson distribution
has to cover 99.99% of the full distribution. Or, put differently, the
cumulative sum of the discrete distribution has to be 0.9999 up to the
point we truncate. I wrote a matlab program
to plot the event number at which the cumulative probability reached
0.999 and 0.9999. The figure (left) shows the results. Keeping only one
event per reaction time step limits us to a mean rate of 0.01 at 99.99%
capture and about 0.03 at 99.9% event capture. For a mean reaction rate
up to about 0.085/time step, keeping up to two events per reaction
captures 99.99% of the events. Keeping three events allows reaction
rates up to about 0.2/time step (at 99.99% capture). So using the 99.99%
criterion, keeping two events instead of one event gives us about an
8-fold speed up, while keeping three events only gives us another factor
of two above the two-event rate.
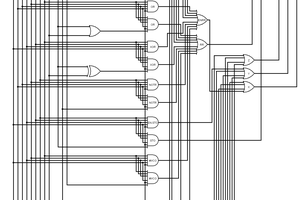
So what do we need to do to implement a maximum of two events? If we model the two reactions as separated in space, and therefore independent, we need to compute the probability of two completely independent reactions separately, then decide if 0, 1 or 2 events occured. If either reaction occurs set the inc/dec outputs to +1/-1. If both occur set the inc/dec outputs to +2/-2. If neither occurs, inc/dec are zero. This seems to be a workable system and was implemented below. A manuscript version of this description is here.
HIgh quality random number s essential for this scheme to work. It is possible to parallelize the linear feedback shift register to get more effective shits per clock cycle. Hoogland, et.al. describe a high quality random number generator designed for Ising model simulation. Using...
Read more » Bruce Land
Bruce Land


 Dave Collins
Dave Collins
 zpekic
zpekic
I did my master thesis of the FHP3 descrete model of fluid dynamics, which only uses bits to represent particles on a hexagonal lattice. Since then, I see differential equations very differently and I am always looking for the microscopic and descrete mechanisms that are often "simplified" by these kinds of equations...
OTOH it has only comforted my mathematical laziness ;-)