- Geometric Constraint Solver. This is a most crucial component which allows to solve a system of geometric constraints applied to a sketch.
- 2D Sketcher. Allows to design 2d sketches applying geometric constraints. Uses HTML5 canvas for rendering.
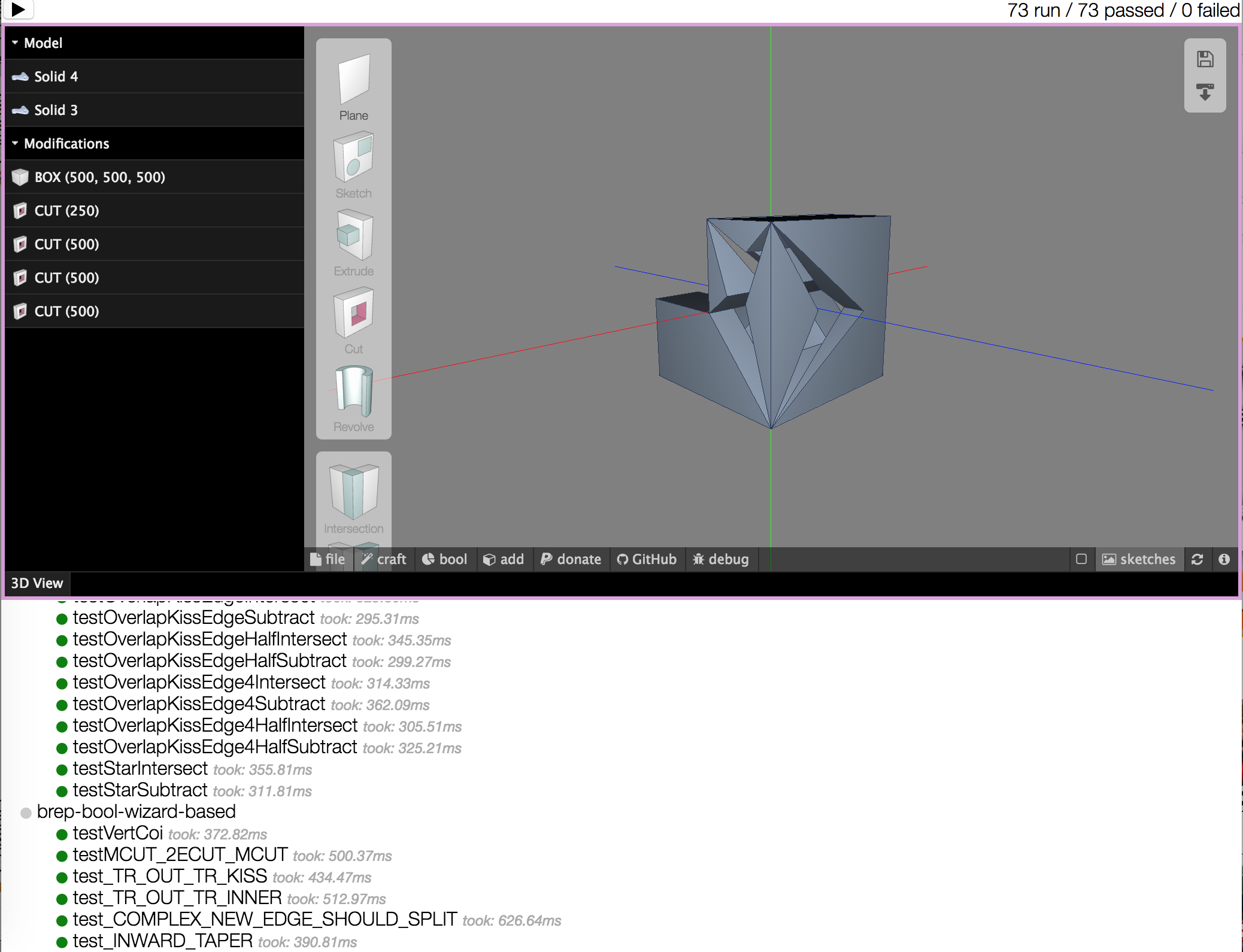
- 3D Modeller. Is used for solid modelling. Uses 2D sketches to perform EXTRUDE and CUT operations on faces of a solid object. Uses WebGL and THREE.js for rendering
- 3D modeller supports navigation over history of modifications where parameters of the craft operations(extrude/cut) could be changed and reapplied again
- Export to STL, DWG and SVG formats
- Saving projects in the browser locale storage
- Repository of dimensions. For example if there is a line length constraint applied, it's not necessary to hardcode some length value. A dimension with a symbolic name can be created and the constraint can refer to that dimension by name. Once value of dimension gets changed the sketch is resolved again accordingly to the new dimension values.
- 2D measurement tool. Allows adding dimensions on a 2D drawing(Linear, Vertical, Horizontal and Arc/Circle dimension are supported)
- No any server-side needed. Only client side Javascript.
jsketcher
Parametric 2D and 3D modeler written in pure javascript
 Val Erastov
Val Erastov




 Francesco
Francesco
 Edgar Bolivar
Edgar Bolivar
 TAIBHSE DESIGNS
TAIBHSE DESIGNS
 Daniel R. Dugan
Daniel R. Dugan
1. is possible add a cnc router engine
2. is possible package it to electron