Introduction
There are three primary methods for developing FPGA designs:
- Verilog
- VHDL
- Schematic Capture
The Hobbyist's Guide to FPGAs will focus on using Verilog to program FPGAs. Verilog and VHDL are both hardware description languages. They allow you to design digital logic circuits by describing them in their language. Verilog was chosen for this guide because it has an easier learning curve and is not quite as picky as VHDL is. There are some that would argue for using VHDL, and for good reason. VHDL has some powerful constructs that Verilog does not. For the average hobbyist, however, Verilog is the right choice and will provide a more pleasant entrance into the world of FPGAs.
Verilog
When designing any system, it is useful to be able to decompose the problem into smaller parts. Digital design is no different. In Verilog we have the concept of modules. A module is a self-contained design that communicates externally through ports. The ports on a module are input and output wires. You could think of a module as it's own standalone logic chip. When we are developing a new design, we start with a module.
/*
* Implements a simple 1-bit half-adder.
*/
module half_adder (
input a,
input b,
output sum,
output carry
);
// sum is the xor of the two inputs
assign sum = a ^ b;
// carry is true only if both inputs are true
assign carry = a & b;
endmodule
The above example is a reusable module that implements a half-adder. It's a nice and simple example that illustrates a few fundamental attributes of Verilog:
- All functionality is implemented within modules.
- Module ports have an associated direction.
- We can directly assign expressions to ports and wires.
- Expressions and comments in Verilog are very similar to expressions and comments in C, C++, and Java.
The assign statement performs a continuous assignment. It's not assigning a singular value to the left-hand side. Instead, it is assigning an expression to the left-hand side. If the value of any components of the expression changes, then the value of the left-hand side wire will change as well. The text of the Verilog translates directly into digital logic elements. If we designed the module as a schematic it might like similar to the one below:
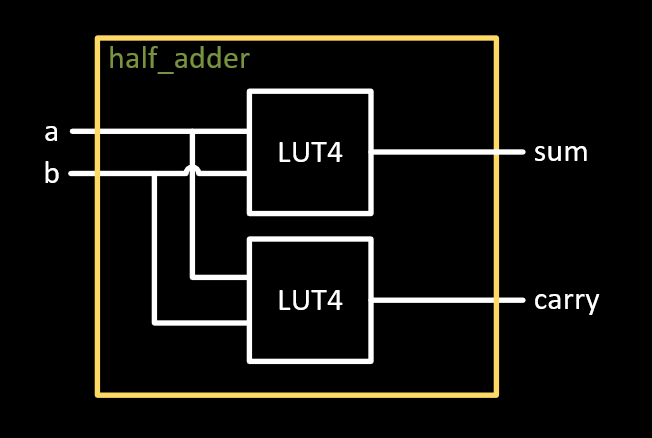
This is an accurate schematic of what the half adder module might look like if it were assembled with logic gates. FPGAs, despite their name, don't actually use logic gates. Instead they use much more powerful LUTs, or Look-Up Tables. In the actual FPGA implementation, the module would look more like the following diagram:
Instead of specific logic gates, the outputs of sum and carry are generated by the LUTs present in the FPGA fabric. The LUTs are programmed to behave like an XOR gate and an AND gate.
Modules can be reused in other modules. We can take our half adder and use it to create a full adder.
/*
* Implements a 1-bit full-adder.
*/
module full_adder (
input a,
input b,
input carry_in,
output sum,
output carry_out
);
// carry outputs from half adders
wire carry_1;
wire carry_2;
// intermediate sum from first half adder
wire sum_1;
// instantiate the first half adder
half_adder ha_1 (
.a(a),
.b(b),
.carry(carry_1),
.sum(sum_1)
);
// instantiate the second half adder
half_adder ha_2 (
.a(sum_1),
.b(carry_in),
.carry(carry_2),
.sum(sum)
);
// generate final carry out signal
assign carry_out = carry_1 | carry_2;
endmodule
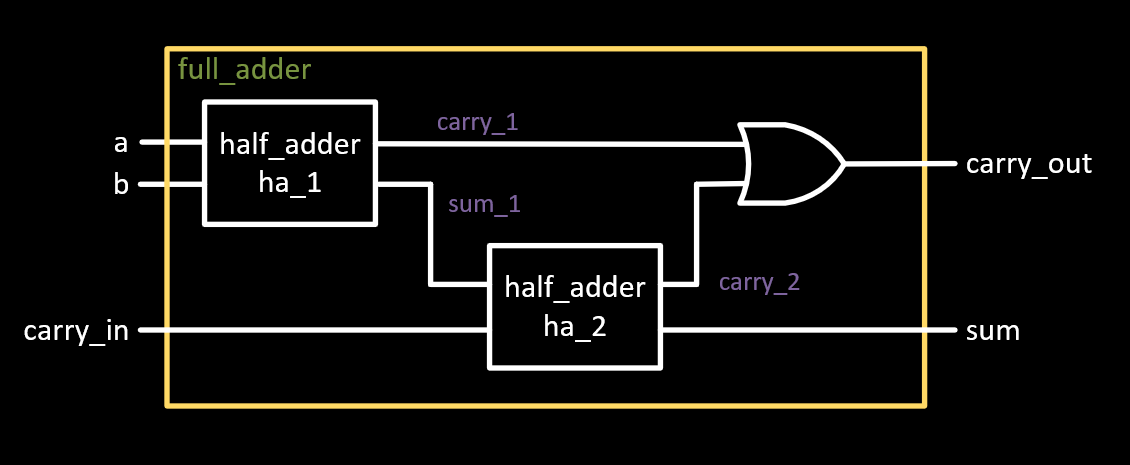
Here we see how modules can be reused and instantiated in another module. First the name of the module type is given, then the name of the instance, then a list of the ports and their connections. We also see that you can create wires internal to the module to connect components within the module.
If this were a schematic it would look like the following diagram:
Pretty neat, but given the amount of Verilog used to describe this simple design and the basic operation of addition we are building up to, you might be asking yourself: "Is this how much work I have to do just to add two numbers in Verilog!?" Luckily the answer is a resounding "No." Implementing an adder just happens to be a useful tool to dive into the most basic concepts of Verilog. Once we know how to implement a useful full-adder the hard way, we can cut to the chase and learn how to do it in a more logical way.
The next extension of this example is to enable larger than 1-bit numbers. This example will start to show the power of using a hardware description language vs. a schematic entry tool.
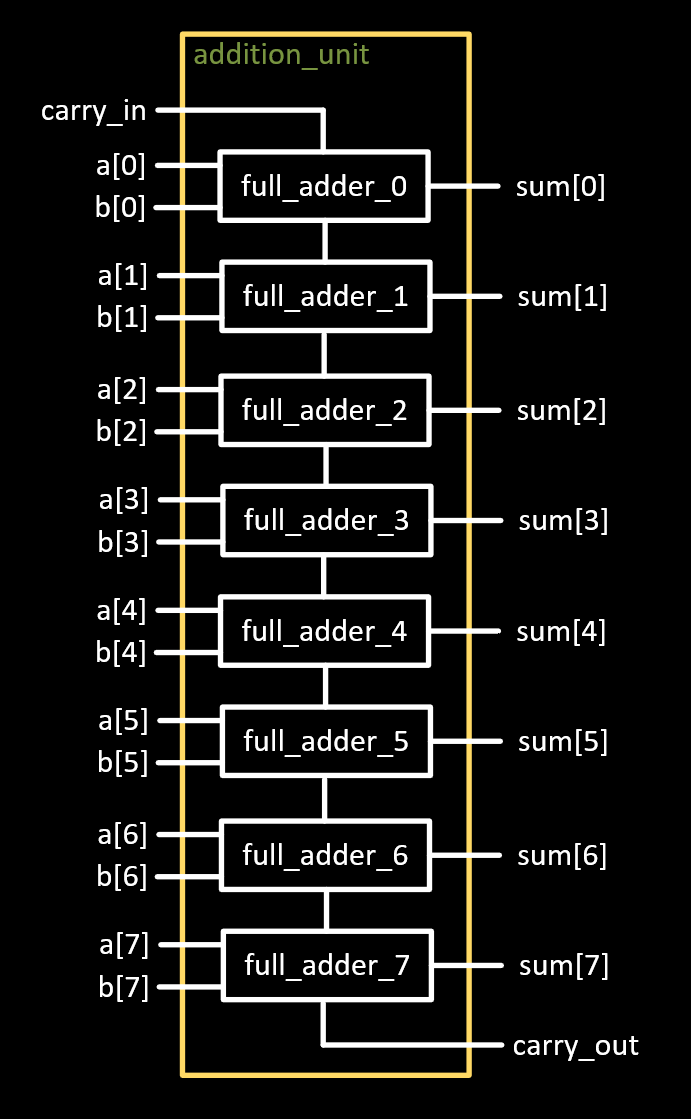
In order to add useful numbers we need several full-adders with a carry-chain connected between them. Let's start with the schematic representation first as the Verilog is going to start getting very interesting:
That's an eight-bit adder. It's pretty cool but it sure took longer for me to draw than I would like to admit. What if we want to expand it to larger or smaller sizes? It is not too convenient. There would be manual work involved in changing the number of bits in the adder. Hardware description languages like Verilog can do a much better job here. Verilog has the concept of module parameters and generate statements that will solve this problem very nicely.
/*
* Implements a configuration addition unit. Set the ADDER_WIDTH
* parameter to the width in bits of the numbers you want to add.
* If no ADDER_WIDTH is specified, then the default width of 8 bits
* will be used.
*/
module addition_unit #(
ADDER_WIDTH = 8
) (
input carry_in,
input [ADDER_WIDTH-1:0] a,
input [ADDER_WIDTH-1:0] b,
output [ADDER_WIDTH-1:0] sum,
output carry_out
);
// these are the wires that will connect the carry output
// of one full adder to the carry input of the next full adder
wire [ADDER_WIDTH:0] carry_chain;
// use a generate block and for-loop to generate as many
// full adders as we need.
genvar i;
generate
for (i = 0; i < ADDER_WIDTH; i = i + 1) begin
full_adder fa (
.a(a[i]),
.b(b[i]),
.sum(sum[i]),
.carry_in(carry_chain[i]),
.carry_out(carry_chain[i + 1])
);
end
endgenerate
// connect carry_in and carry_out to the beginning and end
// of the carry chain
assign carry_chain[0] = carry_in;
assign carry_out = carry_chain[ADDER_WIDTH];
endmodule
There are several new concepts introduced here:
- Module parameters! When you instantiate a module, you can also specify values for any of the module's parameters. This helps you to create reusable modules. In this example we use a parameter to specify the width in bits of the addition operation we are performing.
- Bit vectors. Instead of all wires and ports being one bit wide, we can create wires and ports with as many bits as we want using the bit-slice notation: [msb:lsb]. The indexes used in the bit-slice notation refer to the bit positions and are inclusive. For example: a bit-slice of "a[7:0]" is returning the lower 8 bits of "a".
- Generate blocks and for-loops. Generate blocks allow us to conditionally instantiate modules, assign statements, or always blocks; or even create multiple instances of the aforementioned constructs. In the above example we are using a for-loop in a generate block to instantiate as many full-adders as specified in the ADDER_WIDTH parameter.
A More Logical Approach to Addition
While addition served as an excellent way to describe how to create and use basic modules along with the more advanced concept of generation, this is is not how addition is performed in normal verilog code. There is a much easier way to implement an adder module:
module addition_unit #(
ADDER_WIDTH = 8
) (
input carry_in,
input [ADDER_WIDTH-1:0] a,
input [ADDER_WIDTH-1:0] b,
output [ADDER_WIDTH-1:0] sum,
output carry_out
);
// create an internal sum that includes carry_out
wire [ADDER_WIDTH:0] full_sum;
// use the built-in addition operator
assign full_sum = carry_in + a + b;
assign carry_out = full_sum[ADDER_WIDTH];
endmodule
That's right, there is a built-in addition operator to Verilog. In fact, a standalone module would rarely be used like this in Verilog. It is more common for addition operators to be used in expressions just like bitwise logic operators are.
The FPGA synthesis tools know how to interpret the addition operator and will utilize optimized structures in the FPGA fabric to perform the addition operation. To further illustrate the power of Verilog over schematic entry, let's expand upon our adder concept. Let's create a simple arithmetic logic unit like one that might be found in a simple microcontroller.
module alu #(
ALU_WIDTH = 8
) (
// what type of operation should the ALU perform
input [2:0] opcode,
// input operands
input [ALU_WIDTH-1:0] a,
input [ALU_WIDTH-1:0] b,
// operation output
output reg [ALU_WIDTH-1:0] out
);
// we want to use a combinatorial always block so we can use
// a case statement to decide what to do.
always @(*) begin
case (opcode)
0: out <= a + b;
1: out <= a - b;
2: out <= a & b;
3: out <= a | b;
4: out <= a ^ b;
5: out <= ~a;
6: out <= a << 1;
7: out <= a >> 1;
endcase
end
endmodule
This is a very simple ALU. It is missing useful features like overflow and carry inputs, but I'll leave that as an exercise for the reader to. Now we are introduced to a very important concept in Verilog: the always block. An always block is a block of code that is "evaluated" every time a signal in its sensitivity list changes. In this example I used a * character to make the always block sensitive to all signals it uses.
Without having to write a large amount of code we have a basic arithmetic logic unit. We can add, subtract, perform boolean operations, and shift the input left and right. Not only is all the logic for those operations automatically inferred by the synthesis tools, the case statement will be interpreted as a 8:1 mux as well.
Conclusion
In a short amount of time this tutorial has taken the reader head-long into the fundamental features of Verilog for developing on FPGAs. I sincerely hope this was an enjoyable read. Stay-tuned, the next log will be a hands-on lab taking advantage of the concepts learned here and putting them to use on a hobbyist FPGA board.
To complete the upcoming lab on your own you can use use any of the TinyFPGA boards available at the TinyFPGA Tindie store. If you are deciding on which TinyFPGA to use, please read the user guides for the different boards at tinyfpga.com. The A-series boards need a bit more components to get up and running while the B-series boards are ready to go once plugged into USB.
You will also want a breadboard, some switches you can plug in, LEDs, and resistors for the switches and LEDs. More details about components required will be in the lab itself.
Until next time!
 Luke Valenty
Luke Valenty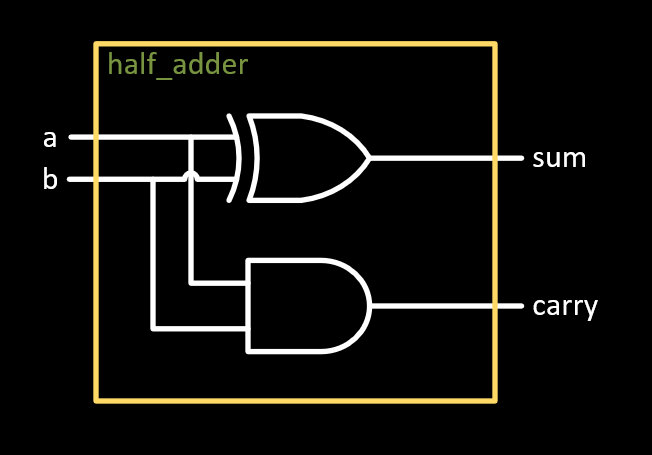
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Excellent write up. FPGAs sound powerful; but daunting. Your write up puts it within the grasps of inspired hobbyist. Hope to see more on this subject. Great work!
Are you sure? yes | no
Thank you for nice tutorial for beginners!!! Hope you find time to continue writing this wonderful tutorial series. Especially, I'm waiting for the hand-on tutorial based on TinyFPGA B2.
Are you sure? yes | no
In module addition_unit wouldn't you need some way of connecting the sum to output sum, maybe
assign sum = full_sum[ADDER_WIDTH-1:0];
?
Are you sure? yes | no
I had the exact same thought - the first example in the “A More Logical Approach to Addition” seems to be missing an assignment to the sum output. I’m a complete newbie to Verilog but I don’t see how that assignment can be implicit.
Hopefully the author can answer, or else correct the example assuming it’s wrong.
Are you sure? yes | no
Excellent Tutorial !!! I have purchased your Tiny FPGA BX and i would like to thank You for it :)
Are you sure? yes | no
Having done Digital Electronics at the University, an approach of this sort makes the TinyFPGA more welcoming. Great series thus far! If there are other places that offer tutorials in this exact manner, please let us know.
Are you sure? yes | no
Another great tutorial. There aren't very many people on the net that explain things a well as you.
Are you sure? yes | no
Excellent tutorial
Hope more is on the way!
Are you sure? yes | no
Excellent introduction to FPGAs, looking forward to reading next articles in the series!
Are you sure? yes | no
Great Job!! I have purchased FPGA's and put off learning how to program till now. I started a long time ago with cpu's made of discreet logic chips so this should stir old memories. Looking forward to the book when your finished till then I'll look forward to the next installment here
thanks for your hard work
Are you sure? yes | no
Thank you! I'd love to see more in this series. A bit surprised I'm the first to say thank you and request more!
Are you sure? yes | no