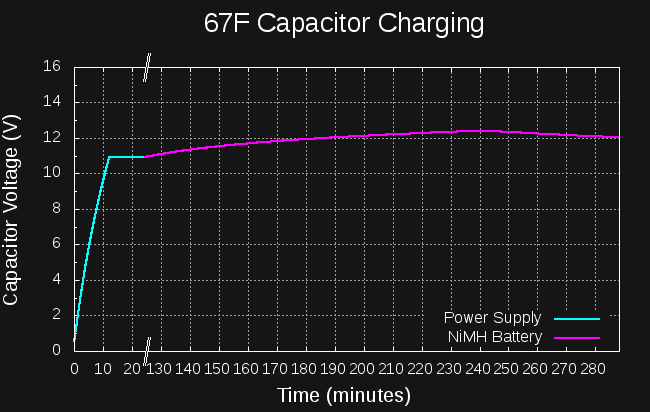
OK, it's not all worked out, yet, but here's the back of the envelope calculations. I found that Mehdi on electroboom has already started a car with super capacitors. He connected 6x 400F capacitors in series to get 66.6 F. This was enough (charged to 14V) to start his car. How much energy is this?
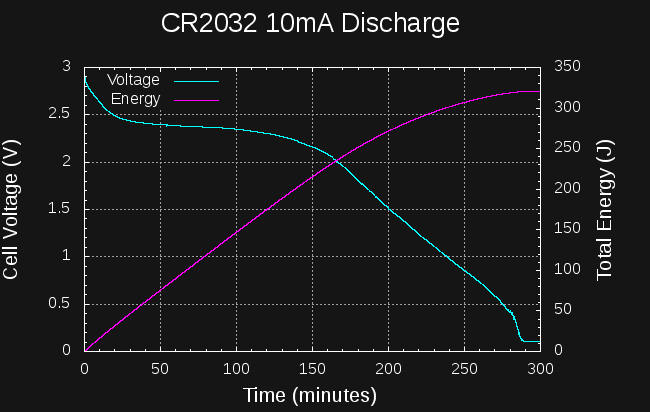
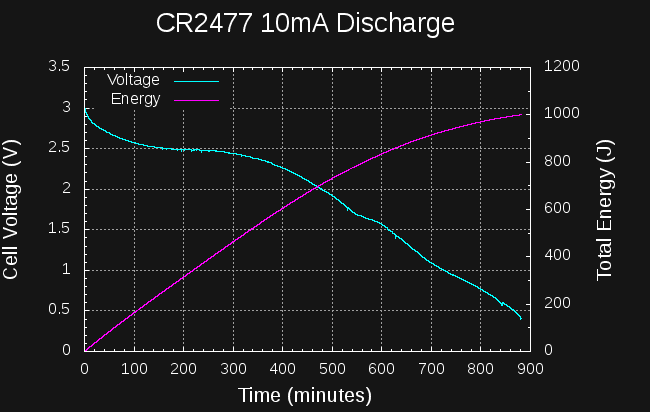
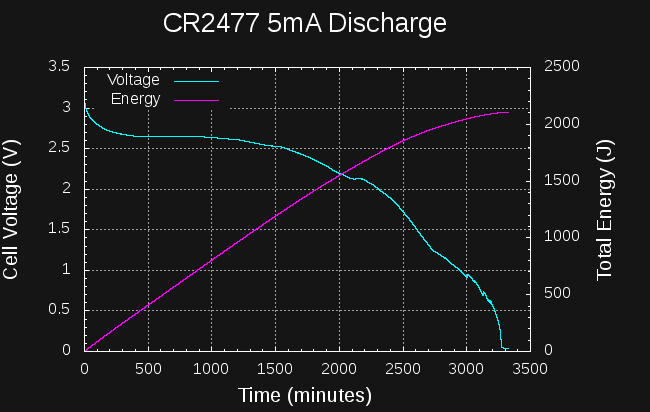
Sounds like a lot. How much energy is in a CR2477 coin cell? They're rated at 1000mAh at 3V:
So, if I can create a boost converter to charge the capacitors to 14V from the cell that's at least 6527/10800 = 60% efficient, I should be able to start a car from a coin cell.
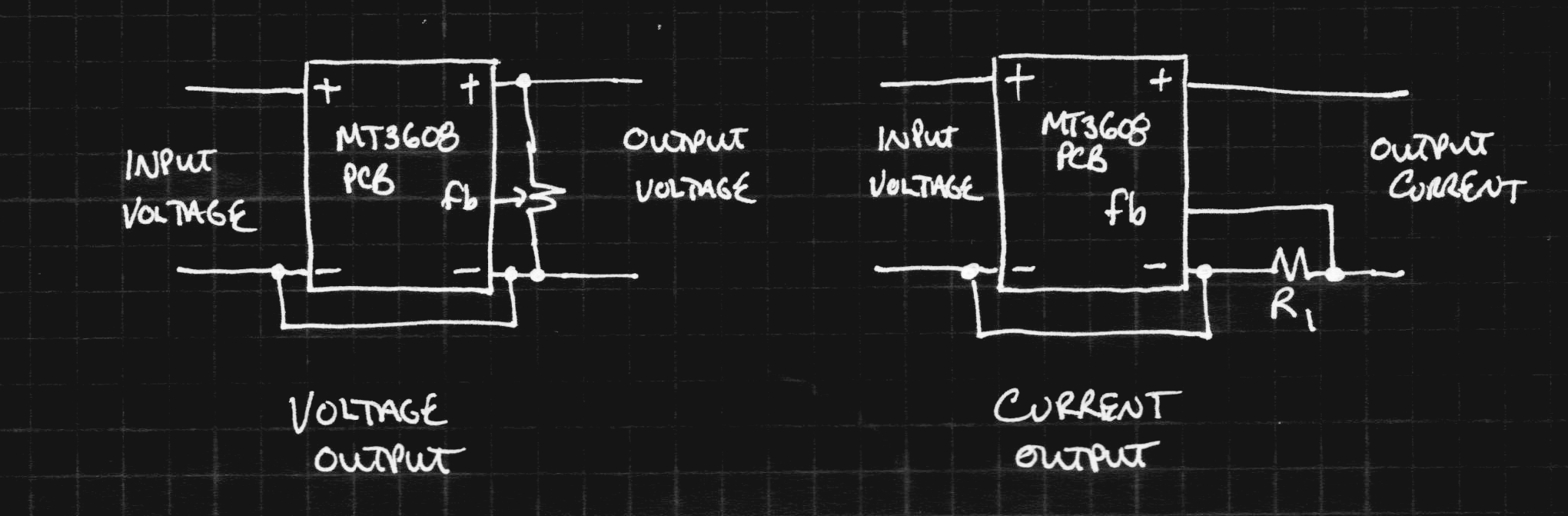
The first rough plan is to make a simple inductor-based boost converter to charge a similar (possibly identical) capacitor bank over perhaps 24 hours, then start the car with the capacitors in place of the usual battery.
Of course, the devil is in the details, but at first look it seems like it could work.
 Ted Yapo
Ted Yapo

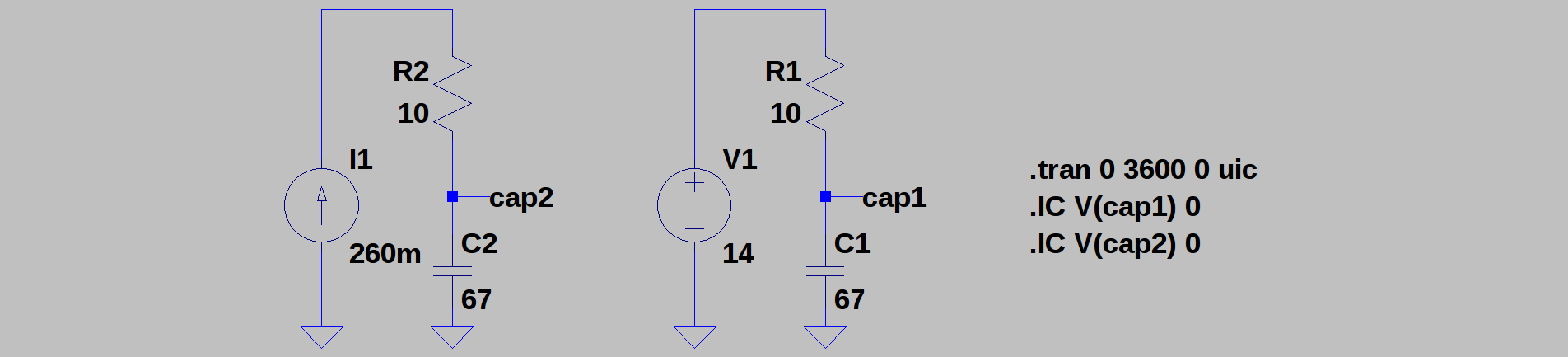
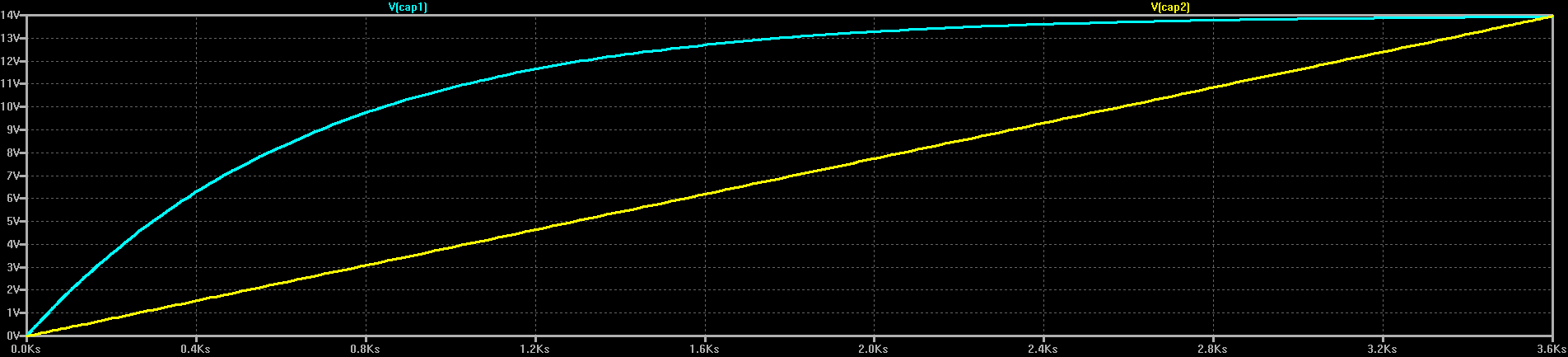
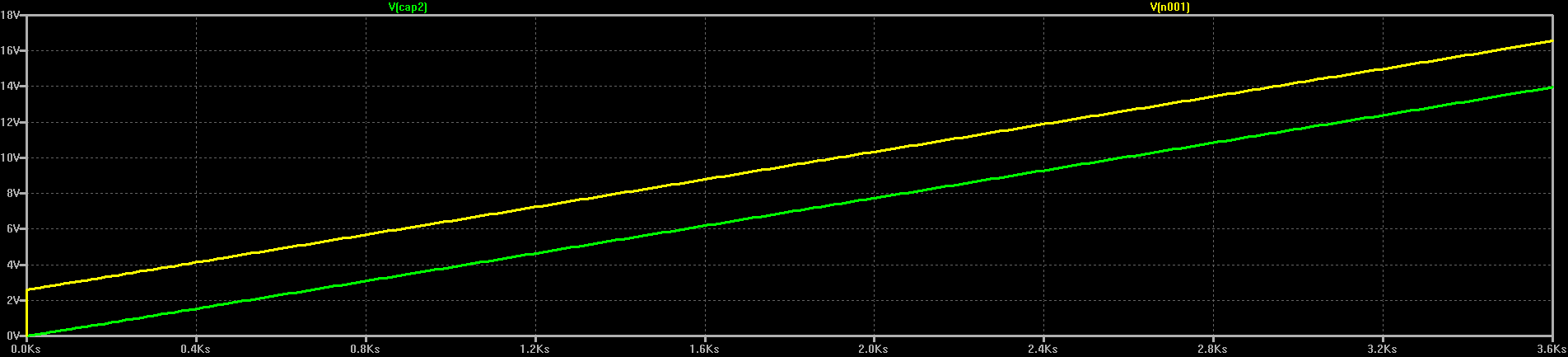




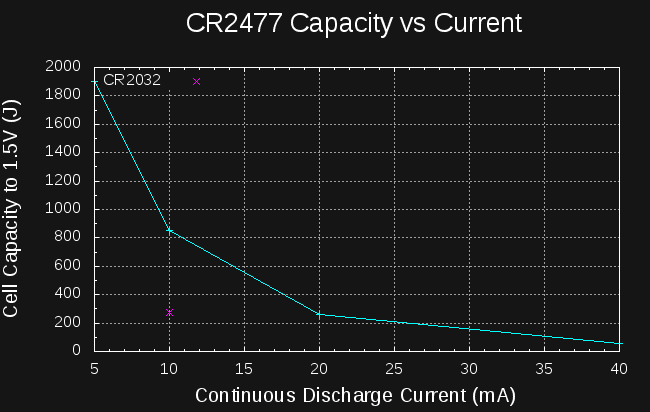
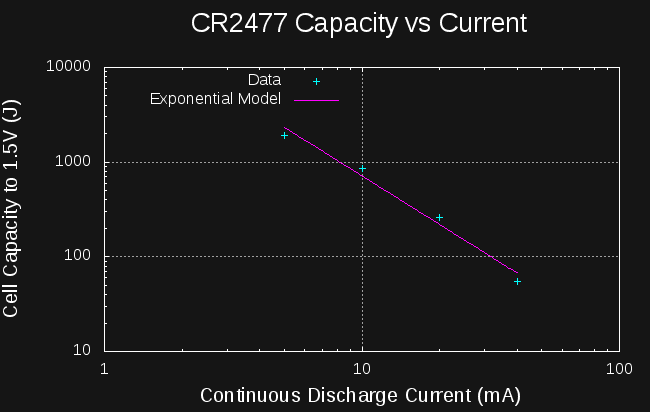
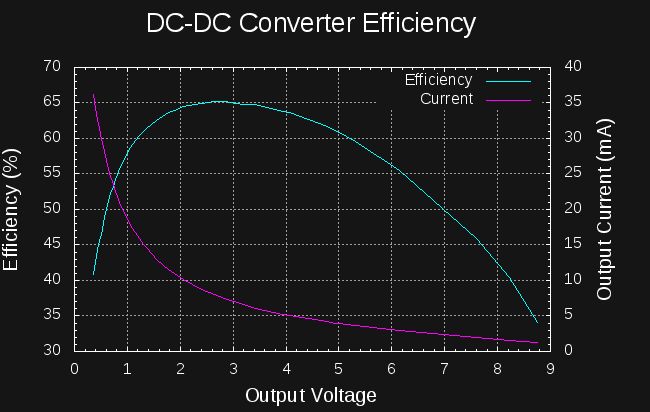
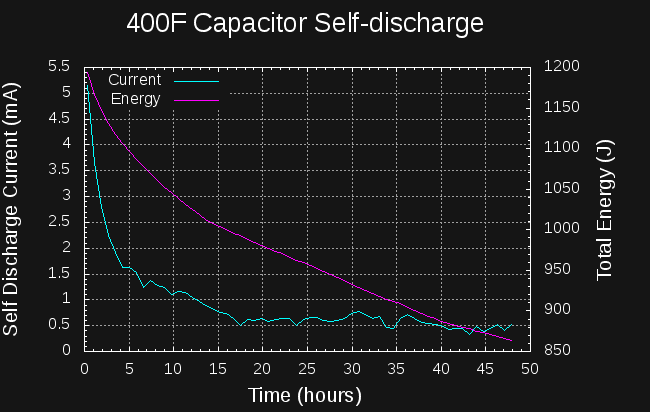













 Patrick Van Oosterwijck
Patrick Van Oosterwijck
 George
George
 jaromir.sukuba
jaromir.sukuba
I am no expert in this field but I do love how you put things and update us, your readers on what going on with the projects. | https://www.goidahoinsurance.com/