I tested a CR2032 cell at continuous 10mA discharge. The results aren't very good.
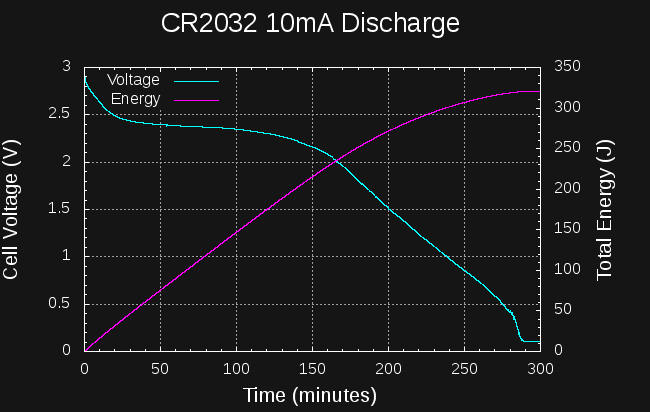
If we take 1.5V as the cutoff voltage, around 275J can be drained from the cell in a little over 3 hours. Draining down to the mV level gets you to 325J in just under 5 hours. This is roughly 12 and 14.5% of the cell's capacity, respectively.
I tried the same experiment with a CR2477 cell:
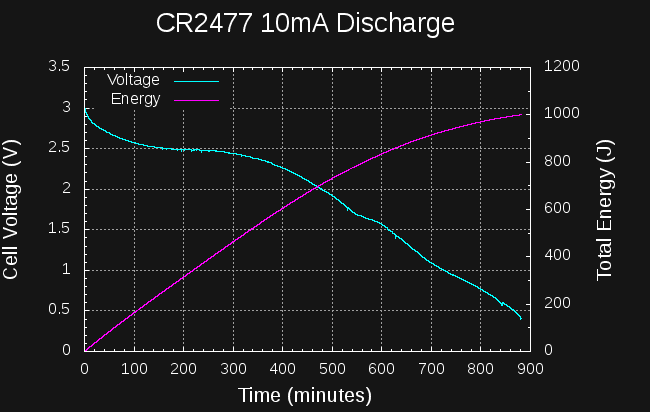
This cell manages about 850J to the 1.5V level in 10 hours. I stopped the test about 15 hours in, when the energy reached 1000J; by this time the cell voltage is below 500mV. This isn't very good either, although it is roughly 3x the energy of the CR2032. The datasheets would have you believe the CR2477 can supply 4x or so at very low discharge rates (1000 vs 225 mAh), so I guess the relative performance of the cells I am seeing roughly makes sense.
I also tried a longer test with a CR2477 at 5mA continuous drain.
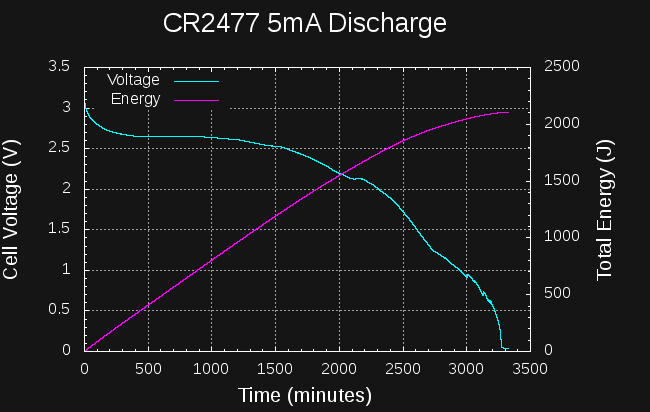
In this case, the cell takes 43 hours to reach the 1.5V level. At this point, it has yielded around 1900J. If you can make used of the cell down to mV levels, you can get around 2100J at this current, but it takes 55 hours. Again, not very good at all.
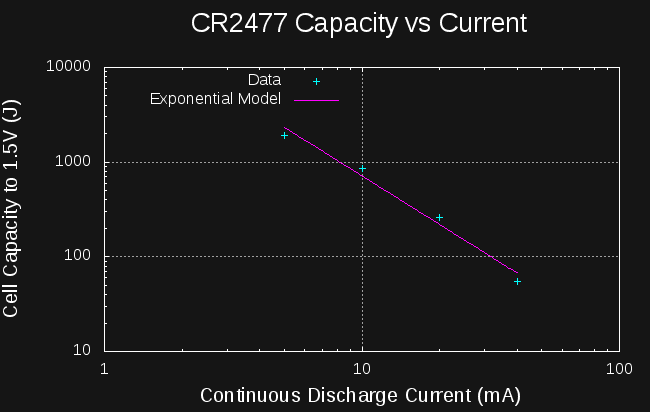
Looking at the four data points I have for CR2477 cells, we can see what effect the drain current has on the yield (I also add the single data point for CR2032):
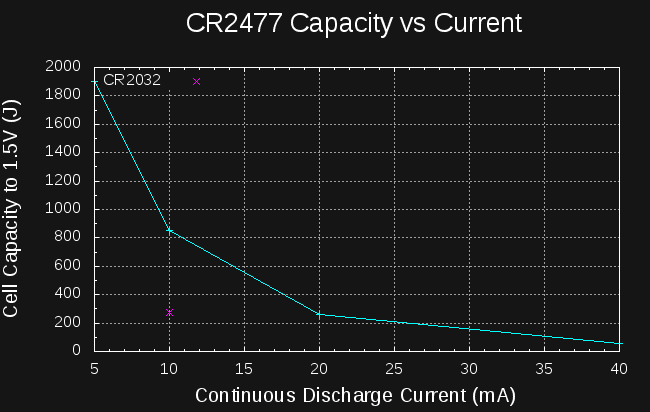
Yield is a very strong function of drain. I wondered how it would look on a log-log scale, so I plotted it, and it is roughly linear, hinting at an exponential relationship between capacity and current drain, similar to Peukert's Law for lead-acid batteries. Here are the data points along with a best fit line in the log-log space:
The exponential model is of the form:
where E is the energy yield of the cell in Joules, I is the discharge current in mA, and k and m constants. For the CR2477, a least-squares fit gives k = 35594, and m = -1.704.
Using this model, I would estimate that at 80mA, you should get 35594*80^-1.704 = 20J, while at 2.5 mA, you should get 35594*2.5^-1.704 = 7469 J.
Just like Peukert's Law, this model predicts you can get infinite energy by draining at lower and lower currents, so at some point it is no longer applicable. Just for fun, I re-arranged the equation to solve for the current you'd need to use to get 9000J (approximately full capacity) from a CR2477. The answer: 2.24 mA. This sounds like an interesting test, and if it wouldn't tie up my meters for five days, I'd start it now. Maybe after the contest :-)
 Ted Yapo
Ted Yapo
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.