-
Care and Feeding of MOSFET Bridges
07/13/2014 at 22:27 • 0 commentsIn this entry we'll look at how to deploy MOSFETs in bridge circuits. (This is also applicable to IGBTs.)
Switch mode electronics are great - they are usually smaller and more efficient than similar linear circuits. However, there are some limitations that we must obey. This log is about how to drive a switch mode MOSFET driver stage.While you're here, could someone please give me a comment about style? Am I writing too much or too little? Too formal?
OK, now let's look at half and full bridge circuits. A half bridge has two switches (Q1 and Q2) and can produce two output voltages: 0 and Vdc. A full bridge has four switches (Q3 - Q6) and can produce three output voltages: -Vdc, 0 and + Vdc. There are some forbidden states which short-circuit the DC link and must be avoided. From a drive perspective, a full bridge is equivalent to two half bridges, so the rest of this article will look at half bridges exclusively.![]()
So, how does a MOSFET work? There is quite a lot of information available online and in textbooks so I'm not going to do a big treatment. If we have a look at the MOSFET with our switchmode hat on, there are 4 distinct modes of operation (not 3 as many textbooks would have it).
It all depends on the gate-source voltage, Vgs, and the drain-source voltage, Vds, and something called the threshold voltage (Vth).
1) Off. This occurrs when the gate-source voltages is below the threshold voltage, i.e. Vgs < Vth
2) Linear mode. This occurrs when the MOSFET is partially turned on. In this mode, the MOSFET works like a current sink. Vgs >= Vth and Vds < (Vgs=Vth).
3) Saturation mode. This occurrs when the MOSFET is fully turned on, and the drain-source path behaves like a resistor - this is the Rds,on parameter that you will find on a power MOSFET datasheet. This also works in reverse - you can 'short circuit' the body diode (this is called syncronous rectification).
4) Diode mode. All MOSFETs have a built in body diode! When Vds is negative (and greater than one diode drop) the MOSEFT will conduct in diode mode. Vds < approx -0.6V.
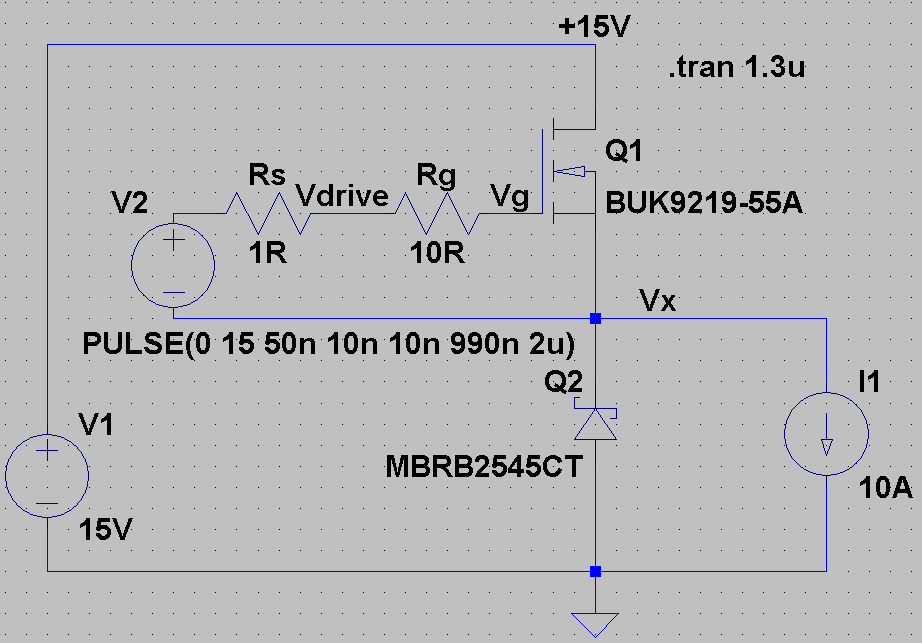
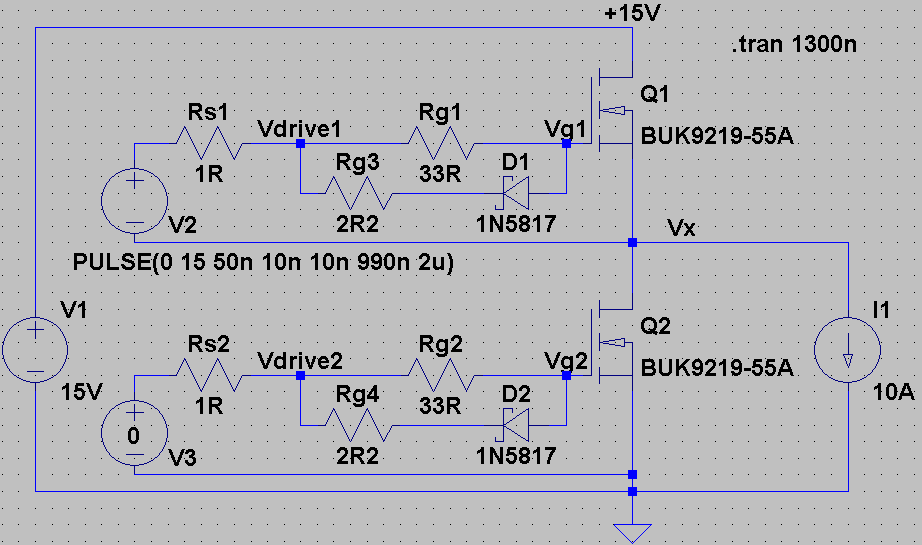
Now let's look at driving a MOSFET. I often use the circuit below to check switching waveforms. V1 is the main DC link (in a real circuit we'll need some capacitors!), V2 is the MOSFET gate driver (15V is a totally standard value, 'logic level' MOSFETs can be driven with 3.3V, 5V or 15V), and I1 is the load (equivalent to a nice big filter inductor, and very useful for evaluating performance in a simple, stable way). Initially, the MOSFET is off, and the diode is on. Vx is slightly lower (one diode drop) than ground.FYI: I picked the wrong MOSFET deliberately to give us some visible 'Miller plateaus.' You can do much better than this MOSFET.
![]()
![]()
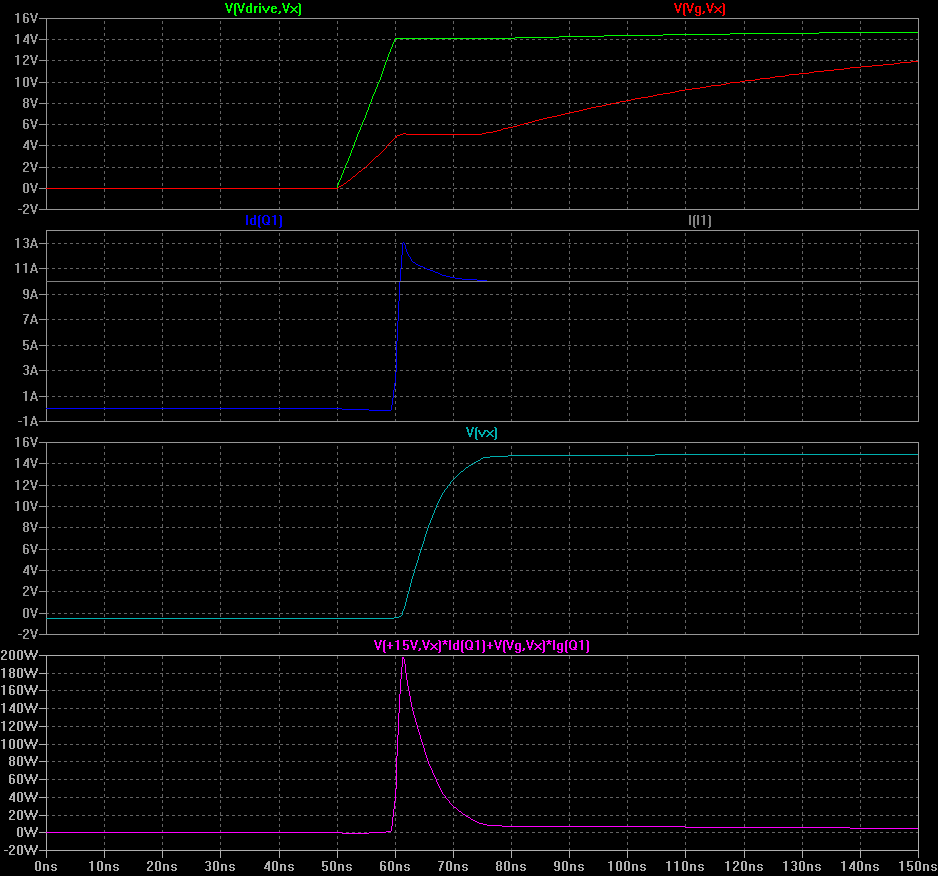
t0 - t1: (50 - 49 ns) When the driver switches on, the MOSFET Vgs climbs (note that there is internal capacitance). The time constant here is set by the internal MOSFET capacitance, the driver series resistance Rs (often in the 1R to 5R range) and the gate resistor Rg.
t1: (59ns) Vgs reaches Vth. Current begins to flow through the MOSFET drain pin.
t1 - t2: (59 - 61 ns) We are now in the linear mode. Current flow through the MOSFET rises. However, the switch node voltage Vx is not rising yet. Vgs continues to rise.
t3: (61 ns) Vgs is now high enough that the MOSFET can deliver the whole load current. Vds begins to fall / Vx begins to rise.
t3 - t4: (61 - 75 ns) Vds falls to zero / Vx rises to Vdc. During this time Vgs is basically flat. This is called the Miller Plateau, and is due to the Miller capacitance between the drain and gate. Current flows through this capacitance (in the 10s to 100s of pF range) in accordance with I = C * dv/dt and provides negative feedback. This is a very useful signal to look for when measuring prototypes.
t4: (75 ns) Vds falls to approximately zero: the MOSFET is turned on.
t4 - t5: (75 ns - 300 ns)Vgs rises a bit more, bringing the MOSFET on resistance down.
We see that quite a bit of power is dissipated in the MOSFET from t1 to t4. This is called the 'turn on loss,' and can be calculated by LTspice by Ctrl-clicking on the MOSFET power channel. Multiplying the turn on loss in Joules by the switching frequency in Hz (i.e. 1/s) gives the average switching loss in W - very useful. The MOSFET turn on loss is 1.1 uJ in this configuration, and the Miller plateau is approximately 14ns long, with an amplitude of 5V.
Wait a moment! The MOSFET current has an extra 3A high bump in it! (Around t = 61 ns) This is due to the reverse recovery and parasitic capacitance of the diode Q2 (Schottky, 45V / 25A). I used a Schottky to reduce the reverse recovery to zero, but it still has capacitance and dissipates about 0.1 uJ during the turn on process.
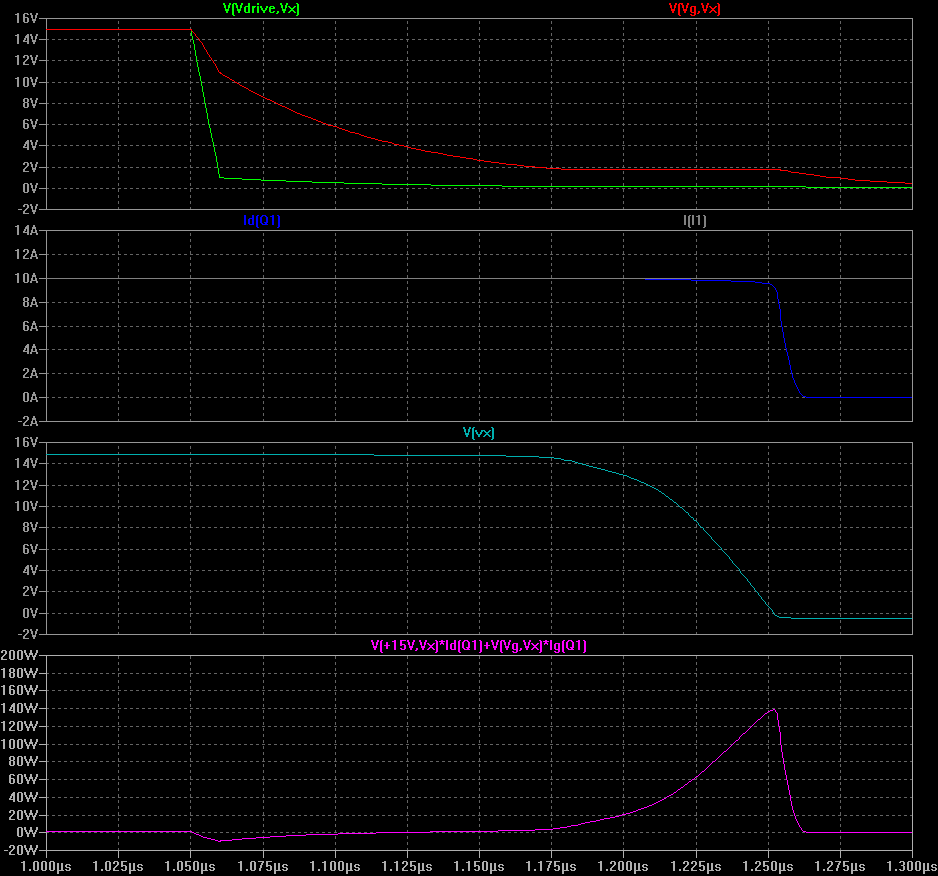
When the MOSFET switches off, the process happens in reverse (and yes, there are turn off losses). The Miller plateau is approximately 75ns long, and the turn-off loss is 4.5uJ - not so good as the turn on!![]() So the total on and off losses in Q1 are approximately 5.6 uJ. We can improve the situation, more on that later.
So the total on and off losses in Q1 are approximately 5.6 uJ. We can improve the situation, more on that later.
Summary: Q1 on+off = 5.6 uJ, Q2 rev. recov. = 0.1 uJ, grand total 5.7 uJ.
HALF BRIDGE GATE DRIVE
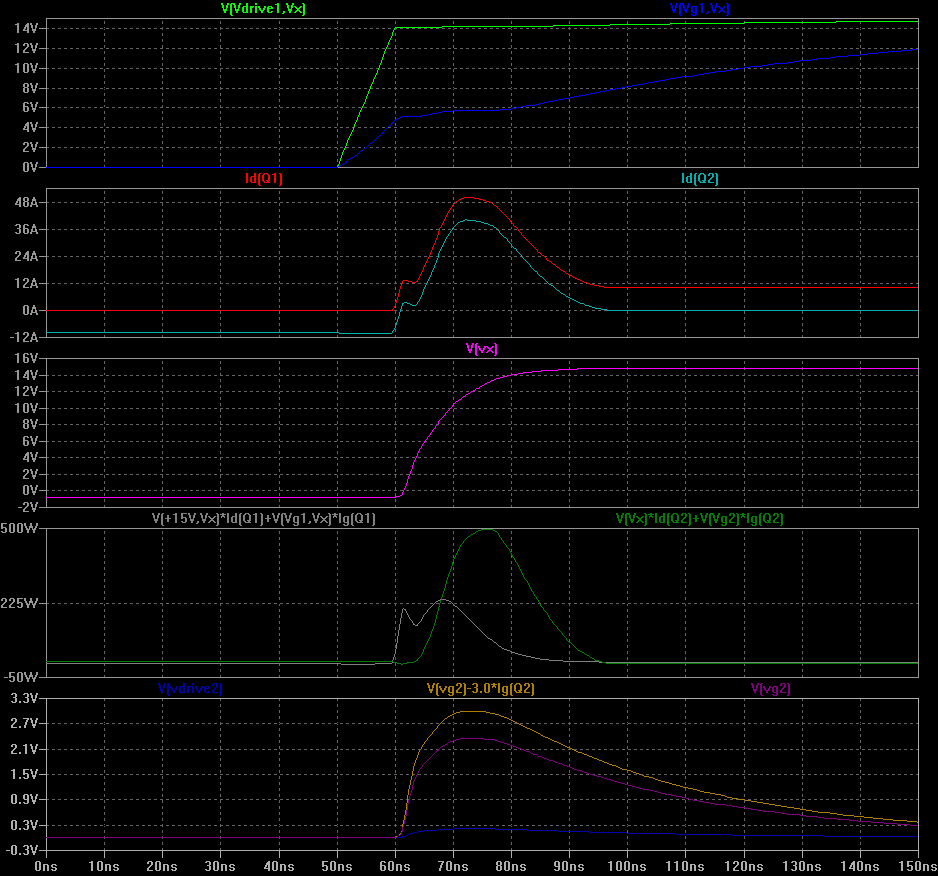
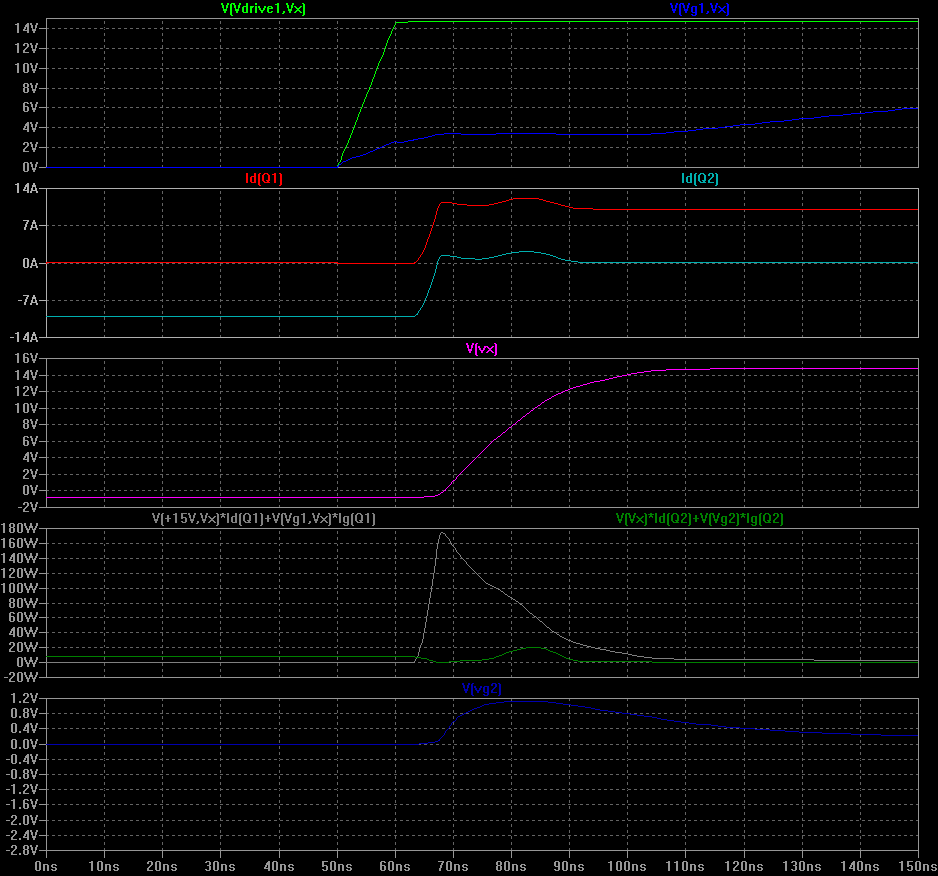
Now let's look at what happens with an actual half bridge configuration. Q2 is used as a diode here.![]()
![]() Turn on of Q1: 3.5 uJ
Turn on of Q1: 3.5 uJ
'Reverse recovery' of Q2: 8.3uJ!!
The Miller plateau is 18ns, and the turn on losses are 3.5uJ in Q1. Why the increase? Because Q2 is misbehaving and has a big curent spike of about 40A (and associated losses thereof ). An essential thing to note is that Vg2 (bottom) does not stay at 0V but actually rises up to about 2V. This is due to coupling of the voltage change in Vx through the Miller capacitance (Cdg) of Q2, through Cdg * dVx / dt. This pushes some current through Q2's gate, and driver doesn't clamp it down hard enough. Q2 actually begins to conduct through the channel (that's where the 40A comes from); this is effectively short circuiting the supply via Q1 and Q2. This is called shoot-through and is very bad news: at best, it causes unneccessary losses. At worst, it
Additionally, these MOSFETs have some internal gate resistance (reading the Spice model, it's about 3 Ohms). If we add a little maths, ("V(vg) - 3.0*Ig(Q2)") we can get the 'effective' gave voltage... and see that it hits around 3.0V, which is definitely turning on Q2 at the worst possible time.![]()
Turn off of Q1: 4.6uJ
Summary: Q1 on+off = 8.1 uJ, Q2 rev. recov. = 8.3 uJ, grand total 16.4 uJ.
During the turn-off of Q1, Q2 has no reverse recovery (there is such a thing as forward recovery, but it's usually negligible) and the switching loss is basically the same as with the Schottky.NEGATIVE GATE DRIVE
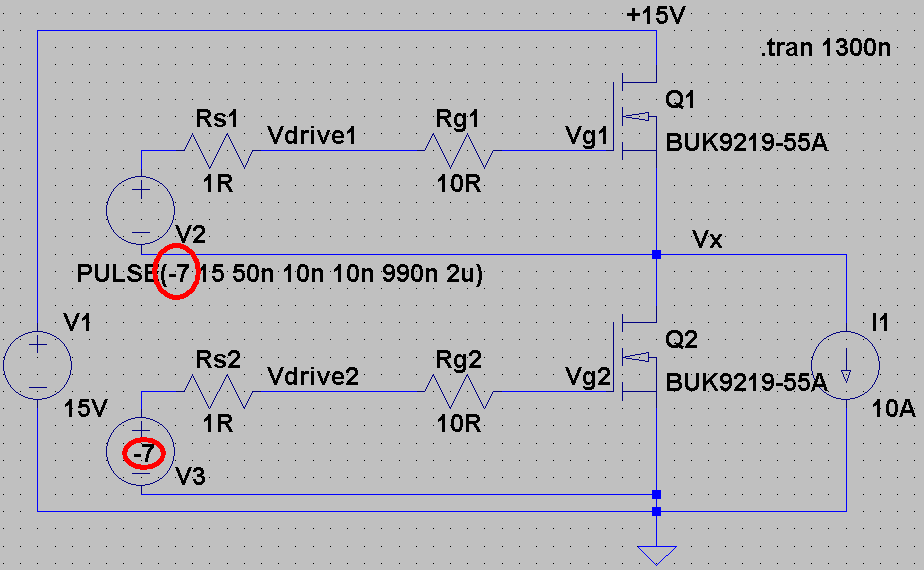
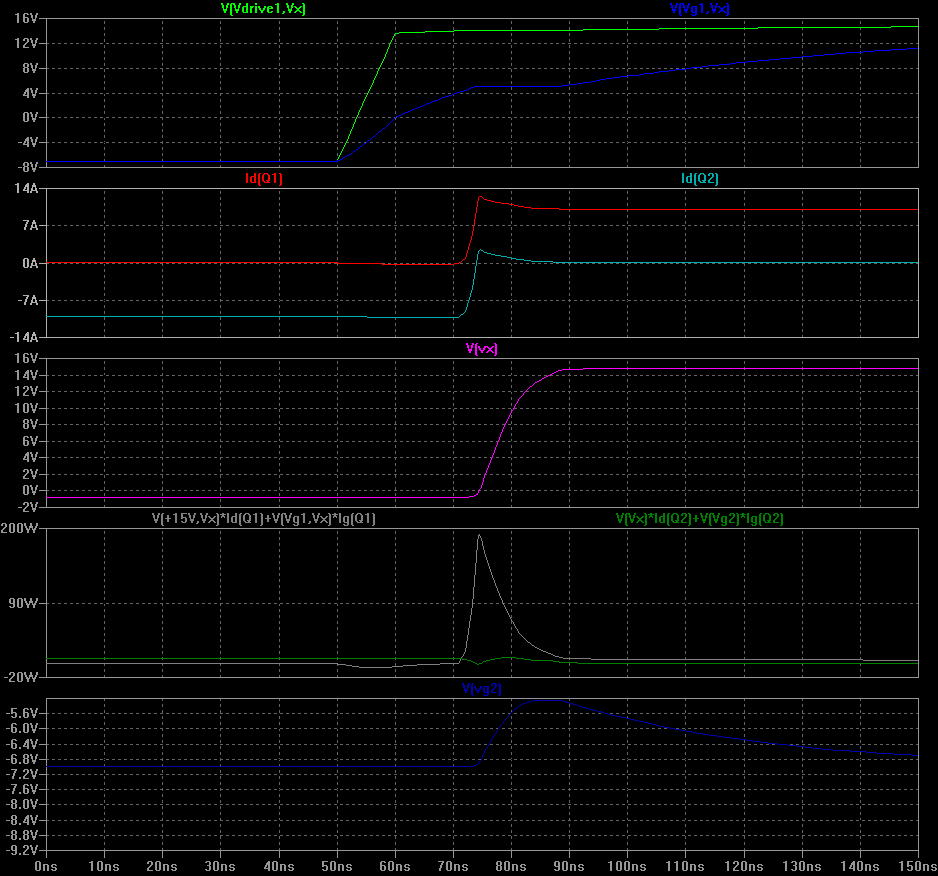
We can use negative gate drive to try to fix Q2's bad behaviour. This involves using -7V/+15V for the gate drivers instead of 0V/+15V (see red circles in circuit diagram). It requires extra circuitry but is really effective. Almost all high power designs (especially those using IGBTs) will use this trick as it gives really good results. The turn-off losses improve too, because more current is available to suck charge out of Q1's gate during turn-off.![]()
![]() Turn on of Q1: 1.2 uJ
Turn on of Q1: 1.2 uJ
Reverse recovery of Q2: 0.3 uJ![]()
Turn off of Q2: 1.0 uJ
Summary: Q1 on+off = 2.2 uJ, Q2 rev. recov. = 0.3 uJ, grand total 2.5 uJ (way better than the previous half-bridge, and even better than the original MOSFET + Schottky).MODIFIED GATE RESISTORS
A cheaper way to address the shoot through problem is to modify the gate resistors, as shown:![]()
How did I select these values? Not so simply, sorry :-(. First, I decided that I would use a medium-large driver chip with a 2.5A 'sink' capability and about 1 Ohm of series resistance (you can find this info in MOSFET driver datasheets, I personally like the Si8233 range from Silabs, but they are a little pricey). Considering a +15V voltage swing out of the driver, with 1R in the driver chip and 3R in the MOSFET, I chose 2.2R for Rg3 and Rg4 to give approx 2.5A turn-off current (note that we really get 10R in parallel with 2.2R, i.e. 1.8R). Then I increased (running multiple simulations) Rg1 and Rg2 until the effective gate voltage (considering the 3R internal resistance!) was around 2.0V. Obviously, if you're doing this for a serious design you need to look in the datasheet at the minimum threshold voltage considering temperature - the threshold often drops with increasing temperature and you must consider that!![]() Turn on of Q1: 2.7 uJ
Turn on of Q1: 2.7 uJ
Reverse recovery of Q2: 0.4 uJ
![]() Turn off of Q2: 2.2 uJ
Turn off of Q2: 2.2 uJ
Summary: Q1 on+off = 4.7 uJ, Q2 rev. recov. = 0.4 uJ, grand total 5.1 uJ.
So, this trick is better than the initial circuit, but not so good as the negative gate drive version. It doesn't need a negative supply, though!
What else could we do to improve matters?- Select a MOSFET with a higher threshold voltage. Many power MOSFETs have a threshold of around 5V which makes controlling shoot through easier.
- Select a driver chip with a 'Miller Clamp' built in, which is specifically designed to address this dV/dt induced turn on problem. Examples include the Avago ACPL-336.
Finally, if at all possible you should measure Vgs and Vds with a good scope (100MHz is marginal, 250MHz is better, and we use 1GHz ones at work) to make sure there's no funny business going on. Also make sure your probe is up to the job, properly connected and properly compensated (I'll try to find a link to a good article for this). If you've really got to be sure, measure Id as well - but you'll need a good current probe. Keep your layout really tight - any inductance in these circuits will lead to additional losses, possible device failure and electromagnetic interference.
At low voltages, MOSFET body diodes are OK in terms of reverse recovery. If you are moving up to higher voltages (say 380V DC), you must be _very_ careful about the reverse recover behaviour of MOSFETs and diodes. A standard MOSFET half-bridge at these voltages can literally explode if you haven't got the gate drive right. Sometimes you find that the turn-on resistors need to be so large (to control reverse recovery) that the switching losses are unacceptable. In this case there are a few things you can try:
1) switch to the CoolMOS CFD types, which have better than average body diodes
2) switch to IGBTs. These devices don't have a body diode (but CANNOT be operated with reverse voltages, sorry) are usually co-packaged with a separate diode chip (usually much better than a MOSFET body diode)
3) modify your topology so that you don't need half-bridges
4) mix MOSFETs and IGBTs (for experts, can be very effective, seen in several high-efficiency solar inverters)
5) use a soft-switching topology that avoids reverse recovery events. -
A Class D Power Amplifier - and Why it Won't Work
07/07/2014 at 04:22 • 1 commentFirst up, apologies for the long drought. I've been super busy at work putting together a MW (yes, MegaWatt) class prototype power converter at work, and it has been eating my life. Now I'm on holiday and finally have a moment to do an update.
So, this entry will be about using a Class D - i.e. switchmode - power amplifier as a controlled current source. Let's have a look at the basic features:
So, V1 is a +15V supply. Q1 and Q2 are small power MOSFETs (driven with synthetic PWM by V2 and V3). L1 and Cf filter the square wave signals at Vx into a pretty smooth voltage at Vy, which feeds our load resistor (RL) via the feedback windings (Lf, actually 1 winding through 3 stacked cores).
The SPICE parameter E is used to adjust the average voltage applied to L1 / Cf / Lf. I have used a .step command here to try several values. I also cheated a bit and forced the initial conditions (IC) of the inductors to avoid long settling times. We get a bit of oscillation between L1 and Cf - this is not a surprise, because we have carefully chosen low resistance MOSFETs, inductors and (presumably) capacitors. Welcome to the wonderful world of power electronics :-)
So we see here that we can achieve controlled currents of 0.2A to 1.0A. However, we actually wanted a +- 1A supply, so this circuit won't work.
Let's have a look at a bipolar version:
So, we now use +- 15V supplies, which means that the MOSFETs now have to block 30V - I've swapped to 55V types. I also added an initial condition (IC) to Cf to cut down on that oscillation, and changed the duty cycle calculation a little.
The duty cycle has 2 changes. Firstly, 0% duty now corresponds to an average of -15V at Vx. 100% duty still corresponds to 15V at Vx. Thus the 0% to 100% gain is now 30V / 100% (where it was previously 15), and there is an offset; 0V occurrs at 50% duty cycle.
The waveforms look promising:
However, there is a subtle and really important problem with the circuit. Let's have a look at the currents into supplies V1 and V4 (i.e. the main suplies). These are equivalent to the drain currents of Q1 and Q2 (bottom).
So, the average current through Q1 is 545mA, and the average current through Q2 is -435 mA. What does this mean?
Well, positive current through Q1 corresponds to real power (8.20W) being drawn out of V1. This is what we expect. Negative current through Q2 corresponds to real power (6.52W) being pushed into V2. This is fine in SPICE, where the voltage source is perfect. However, a normal power supply cannot absorb power. This means that energy will build up in the filter capacitors, increasing their voltage until something A) stops working or B) blows up.
I personally prefer option A, so I like to put proteciton in place. Got some spare ADC channels? Add software overvoltage protection. Got no ADC channels? Add comparators. Your hacking time is valuable, people! Don't spending it fixing avoidable mistakes when you could be making new and exciting mistakes.
Note: negative current through a MOSFET is absolutely possible. Firstly, all enhancement mode (the normal type) MOSFETS, be they N ot P channel, have a built in body diode. Secondly, if you apply gate voltage, the channels do turn on and conduct. This is called synchronous rectification and is often used by power supply designers to improve efficiency.
What about negative current, you ask? Well, re-running the sim yields:
I(Q1) = -471 mA average (7.07W pushed into V1)
I(Q2) = 536 mA average (8.04W supplied by V4).So, we have a mirror image of the same problem. V1 blows up instead of V4. This is an inherent problem with the circuit. I have done the paper anaylsis too (but didn't want to bore you all with the maths - let me know if you're interested) and this is exactly the case. For a non-zero output current we have inconvenient energy transfer between the positive and negative power supplies.
But wait! Class D audio amps work! What gives?
So, the answer to this one lies in the application. An audio amp is carefully designed to deliver zero DC current at the output (as this could damage the speakers). Therefore the average power transfer between the positive and negative power supplies is approximately zero. There is of course some transient power transfer, but we can buffer that with some big storage capacitors.
The next installment will cover a couple of potential solutions to this problem.
See you all later. -
Pulse Generation Circuits
03/31/2014 at 10:48 • 0 commentsIn the last posts we saw how a fluxgate works in simulation. Simulations are all good when you can just add a pulsed voltage source - everything is perfect. In the real world, we have some challenges:
1) We need very low DC offset to avoid adding DC offset to the sensor.
2) We need a modest power capability to excite the fluxgates. I'm looking at around ±12V @ 250 mA, which requires some care.
3) Because the ferrite cores of the fluxgates are not identical, I would like a way to adjust the voltage level and timing of the outputs.
DC offset
This one's easy: add a DC blocking capacitor. I did some sims and found that a 10 uF cap seems to be OK. Given that this cap will have a bit of ripple current (max 250 mA RMS) and could see negative voltage, I would use film or chip ceramic types here - not electrolytic.
This is not to say that an appropriate electrolytic wouldn't work, but it must be chosen carefully.
Power capacity
There are 3 options here: 2A) high power op amp, 2B) opamp with external buffer, 2C) MOSFET driver stage.
2A) we can just buy a high power op amp. However, these critters can be expensive, unavailable, or only come in inconvenient packages. Cooling could also be an issue.
2B) An opamp with an output buffer a good option.
We can take a common op amp (here a TL071) and add a pair of Bipolar Junction Transistors (BJTs) as an output buffer.
So, what are the components doing?
- U1 is a TL071 opamp and functions as a voltage amplifier.
- Q1, Q2 form a complimentary emitter follower (current amplifier).
- R1 limits base current into the BJTs and should (hopefully) help keep things stable.
- Rf and Rb provide voltage feedback to the opamp. Note that Rf is connected to the output Vo, so the voltage drops in Q1 and Q2 are automatically compensated.
- C1 provides negative feedback at high frequency to provide stable operation of the opamp.
- V3 is the pulse source.
Success! Note that we will dissipate some power in Q1 and Q2 - we need to consider this later.
Let's have a look at what C1 does. Below is a plot of the rising edge at t = 0.5ms with varying values of C1 (10pF (green), 20pF, 50pF, 100pF, 200pF, 500pF (grey)). As the value of C1 goes up, things slow down. We also see a 'bump' around 501us - this is caused by the output voltage rising above 0V, which means the output current changes from negative to positive, and therefore we must transfer the current from Q2 to Q1. This is crossover distortion, and is a big deal if you want a HiFi amp, but probably not a problem here.
Note: we could use a single +30V supply rail and rely on the output coupling cap (not shown here) to give us 0V DC. However, I expect to need ±15V rails later in the game.
2C) A MOSFET driver looks like a good option. We would get a good square output with low power losses (especially as we will have a switching frequency around 4kHz -> basically no switching losses!). As an added bonuse, we have a
Have a look at the LT website to get an idea of what's involved. I'm not going to bother simulating this because there's a problem... we can only control the amplitude of the pulse by adjusting the DC supply rails. This means extra DC-DC converters (or linear regulators) which is a pain.
Time / Voltage Trimming
The two ferrite cores used for the fluxgates will not be identical. Hopefully they will come from the same batch and be similar, but identical is too much to hope for. Therefore we should be able to adjust the voltage levels and pulse timing independently for each channel.
Adjusting the timing of the pulses is pretty similar for option 2B and 2C.
Adjusting the voltage levels of the pulses is not. For option 2B, we can simply use a couple of Digital to Analog Converters (DACs) to our system controller. For option 2C, we would need separate, independently regulated power supplies. This is a pain.
Therefore I am going with option 2B; opamps with output buffers.
Until next time
jbb
- U1 is a TL071 opamp and functions as a voltage amplifier.
-
Closed Loop Fluxgate (v0)
03/11/2014 at 12:25 • 1 comment(Edited by jbb 21/3/14 for typos)
As we saw in the previous two posts, we can use a fluxgate to measure an unknown primary current. The use of two fluxgates provides (partial) cancellation of induced ripple Electro Motive Forces (EMFs) in the primary circuit.
However, we also saw that the current range of the fluxgate sensor is limited to around half of Isat (see project log 1), i.e. about 3A. We want a measurement range of around ±25A, so we have a problem - the sensor is only good for 10% of the desired range!
Additionally, we want the induced voltage Ep to be as low as possible, which happens when Ip = 0 (see project log 2).
The solution to both problems is closed loop control. We will add a third feedback winding with Nf turns. This gives us a pair of 3 winding transformers as shown:
![]() We now have an extra degree of freedom to play with: the current through the feedback windings If. With a bit of closed loop control, we can adjust If such that:
We now have an extra degree of freedom to play with: the current through the feedback windings If. With a bit of closed loop control, we can adjust If such that:- NpIp + NfIf = 0 (approx)
With a little manipulation:
- If = Ip * Np / Nf
- For Nf = 25, we need to drive If with between -1A and +1A.
This will yield 0V output from the fluxgate current sensor, and 0V of induced voltage Ep. The model is shown below:
![]()
A few points:
- We are using a 2A input current
- I'm using ±5V for the analog stages as it's easier to get good opamps at this voltage level.
- U1 (LTC1992) is a fully differential op amp. This means that it produces 2 output voltages - one 'positive' and the other 'negative' (this output has the circle to show negation).
- I'm using an LT203 as the
demodulator - note how it uses the 'positive' and 'negative' outputs of
the opamp to do a multiplication by +1 or -1 (modlled here as voltage-controlled switches S1 and S2, also note the .model LT203 entry).
- U2 is a low pass filter. Note that this opamp must have low bias current (which would cause voltage offset when passing through R5 and R6), low offset voltage and (hopefully) low noise.
- U3 forms a PI controller. R8, R9 and C7 set the parameters. The maximum output voltage is fixed by the ±5V supply rails to approx. ±5V.
- G1 is an ideal voltage-to-current converter. The gain of 0.2 means that 5V (maximum PI controller output) produces 1A (maximum required If). There will be a future post about how to actually build one of these.
So, let's have a look at the waveforms:
![]() We see that:
We see that:- Vz (output of the PI controller) is stable :-)
- On the 2nd plot: the feedback current If (here -25*I(G1)) equals tracks the input current Ip * Np. I didn't run the sim for long enough to fully settle, but it does. This demonstrates that we do get Ip*Np = Is*Ns i.e. current transformer behaviour.
- Current I(L1) shows the 'total' current applied to a ferrite core, i.e. NpIp + NeIe + NfIf.
- The output of the fluxgate sensor + lowpass filter (Vy) settles to 0, as expected.
- Not shown: Ep is nice and low.
Fantastic, we have a working DC current sensor! Now what about 50Hz AC?
![]() Well, after a few ms of transient behaviour at startup, we do get a sinusoidal current out. However, we have quite a bit of phase shift (power measurements using this would be useless!). In a future post we will talk about bandwidth extension with a third ferrite core functioning as a current transformer.
Well, after a few ms of transient behaviour at startup, we do get a sinusoidal current out. However, we have quite a bit of phase shift (power measurements using this would be useless!). In a future post we will talk about bandwidth extension with a third ferrite core functioning as a current transformer.Next post: practical excitation circuits for the fluxgate.
- NpIp + NfIf = 0 (approx)
-
Two-core Fluxgate
03/10/2014 at 08:18 • 0 commentsMy last project entry described a single-core fluxgate, and showed that it can measure primary currents. It also showed that the fluxgate injects a few hundred mV of ripple into the primary circuit. This entry describes a two-core fluxgate which offers reduced ripple injection into the primary.
First up, let's ask where this injected voltage (I'm calling it Ep, short for 'EMF injected into the primary' (EMF = Electro-Motive Force)) comes from. As we saw in the previous post, it is a funny-shaped waveform with a 5 kHz fundamental frequency. This is a dead giveaway; the only 5 kHz singal source around is the excitation supply. Therefore we deduce that Ep is caused by the transformer action of the fluxgate. We cannot avoid this action, because we have to excite the fluxgate in order to measure anything.![]() But we can compensate for it. We can do this by adding an opposing EMF to the circuit. A good way to do this is to add a second fluxgate with opposite 'polarity' to the first as shown:
But we can compensate for it. We can do this by adding an opposing EMF to the circuit. A good way to do this is to add a second fluxgate with opposite 'polarity' to the first as shown:![]() We now have a vastly reduced Ep term - theoretically zero (we will have a look at component tolerances later). Also, we now have the opportunity to measure the difference between Vm1 and Vm2, which we see is (in principle) zero Volts at zero primary current:
We now have a vastly reduced Ep term - theoretically zero (we will have a look at component tolerances later). Also, we now have the opportunity to measure the difference between Vm1 and Vm2, which we see is (in principle) zero Volts at zero primary current:![]() And if we have a 1A primary current Ip, we get some nonzero quantites: the voltage between Vm1 and Vm2 is nonzero and Ep is nonzero.
And if we have a 1A primary current Ip, we get some nonzero quantites: the voltage between Vm1 and Vm2 is nonzero and Ep is nonzero.![]() If we sweep Ip over a -3A to +3A range (this is the X axis), and look at the average of Vx (i.e. output of a low pass filter) and the RMS value of Ep, things look pretty good:
If we sweep Ip over a -3A to +3A range (this is the X axis), and look at the average of Vx (i.e. output of a low pass filter) and the RMS value of Ep, things look pretty good:![]() Our current to voltage gain has doubled, and Ep is vastly reduced compared to the original 320 mV RMS. In fact, it should go to zero when Ip = 0 (note that component tolerances are not yet considered). So, we have gotten both more output signal and less voltage injection into the primary circuit, which is most welcome.
Our current to voltage gain has doubled, and Ep is vastly reduced compared to the original 320 mV RMS. In fact, it should go to zero when Ip = 0 (note that component tolerances are not yet considered). So, we have gotten both more output signal and less voltage injection into the primary circuit, which is most welcome.I must confess, I avoided one imporant issue in the first post: current measurement range. I mentioned in the project description that I was interested in a 25 A range. Let's simulate that...
![]() Oh ****. Our sensor is nice and linear in the -3A to +3A range, but all kinds of nonlinear outside that (not sure what the glitch around +12A is, but I don't like it). This is not going to work as desired.
Oh ****. Our sensor is nice and linear in the -3A to +3A range, but all kinds of nonlinear outside that (not sure what the glitch around +12A is, but I don't like it). This is not going to work as desired.
The solution: closed-loop current sensing.
See you next time
jbb -
Single Core Fluxgate
03/09/2014 at 12:26 • 2 commentsSo, first entry.
I normally write formal reports or academic papers, which are really dry and cannot contain pronouns (no really). Ahem: Under normal circumstances, the authors avoid the use of pronouns for stylistic reasons.
Here I don't have to be so formal, but you may see some horrible academic-ese from time to time. Sorry in advance.
I'm not going to rehash how fluxgates work in detail, because there's some good informaiton online. Usually it's about measurements of magnetic fields (see How a fluxgate works and DCCT Technology Review), but as we know, the current flowing through a primary conductor will generate a magnetic field, which we can then measure. Excellent.
The heart of a fluxgate is a saturable inductor. All magetic materials (iron, iron powder, ferrite etc.) saturate, so I chose a material that: comes in a toroidial shape, has high permeability (i.e. magnetises easily) and can actually be ordered from a distributor. This is the Epcos B64290L0618X038 (available from DigiKey).
The basic parameters we will use for this toroid are:
- AL : the inductance of one turn on the core : 5.086 uH
- Hsat : the saturation Magneto Motive Force (MMF) : 100 A / m
- le : the 'effective' length of the magnetic path around the toroid (a sort of 'average circumference'): 60.07mm
From this we can work out how much current will saturate the core:
- Isat = Hsat * le
- Isat = 6.007 A
This is valid for our one turn primary, but our secondary winding will have more than one turn. Armed with a number of tunrs, we can calculate some useful values:
- Ne : number of excitation turns : 50
- Wire size: 0.315mm diameter
- Le = Ne^2 * AL = 26.8 mH
- Isat,exc = Isat / Ns = 120.1 mA
- Re = 0.5 Ohm (approx, calculated from turn length of 36mm).
- (11/3/2014: renamed Ns to Ne etc. for compatibility with future posts.)
We can now do a bit of modelling with LTspice. I thoroughly recommend this program - it's high quality, and freely available from Linear Technologies. They don't even make you create an account to get it. Here we go:
![]() V2 provides the excitation square wave.
V2 provides the excitation square wave.Rexc1, E1, V1, F1 and L1 model the 'excitation' winding. V1,E1 and F1 are used to refer the excitation-side voltages and currents to L1 (not necessary here, but we'll need it later). L1 is a saturating inductor model (it's not perfect but should be good enough...).
We see that the current through R1 has some sharp peaks. These show that the core saturates as expected. Also note that Ep - the equivalent primary voltage - is a bit spiky and nasty. More on that later...
What happens when we add some primary current? I have added a current source Ip, and a .step param command to apply -3 to +3 A of primary current in 1 A steps. It turns out that the average current is always 0 (because of C1) but the shape of the current waveform changes.
![]()
The solution to this problem is to demodulate the measured voltage across R1. We're using a square wave at the 2nd harmonic (i.e. 10 kHz) Vdem and multiplying it by the voltage across the sense resistor Vm1 to form a nasty complicated-looking waveform Vx. Fortunately, it looks like Vx has a DC component.
![]() By adding some .measure commands to the Spice file, we can plot the average (i.e. DC component) of Vx against the applied Ip. This averaging can be implemented using a simple low pass filter. We are now getting something like 1 V / A gain - excellent.
By adding some .measure commands to the Spice file, we can plot the average (i.e. DC component) of Vx against the applied Ip. This averaging can be implemented using a simple low pass filter. We are now getting something like 1 V / A gain - excellent. However, there's a problem: the induced voltage Ep. We see here that we will induce about 320 mV (RMS, not a sine wave!) back into the primary circuit. This is going to be a big problem if we're trying to do some measurements on a 12 V system.
![]() Next time we will look at a double core fluxgate to show how we can reduce Ep significantly.
Next time we will look at a double core fluxgate to show how we can reduce Ep significantly. - AL : the inductance of one turn on the core : 5.086 uH
DC Current Transformer
Investigating fluxgate current sensors (DC capable) with detours into analog electronics and switched mode power supplies.
 jbb
jbb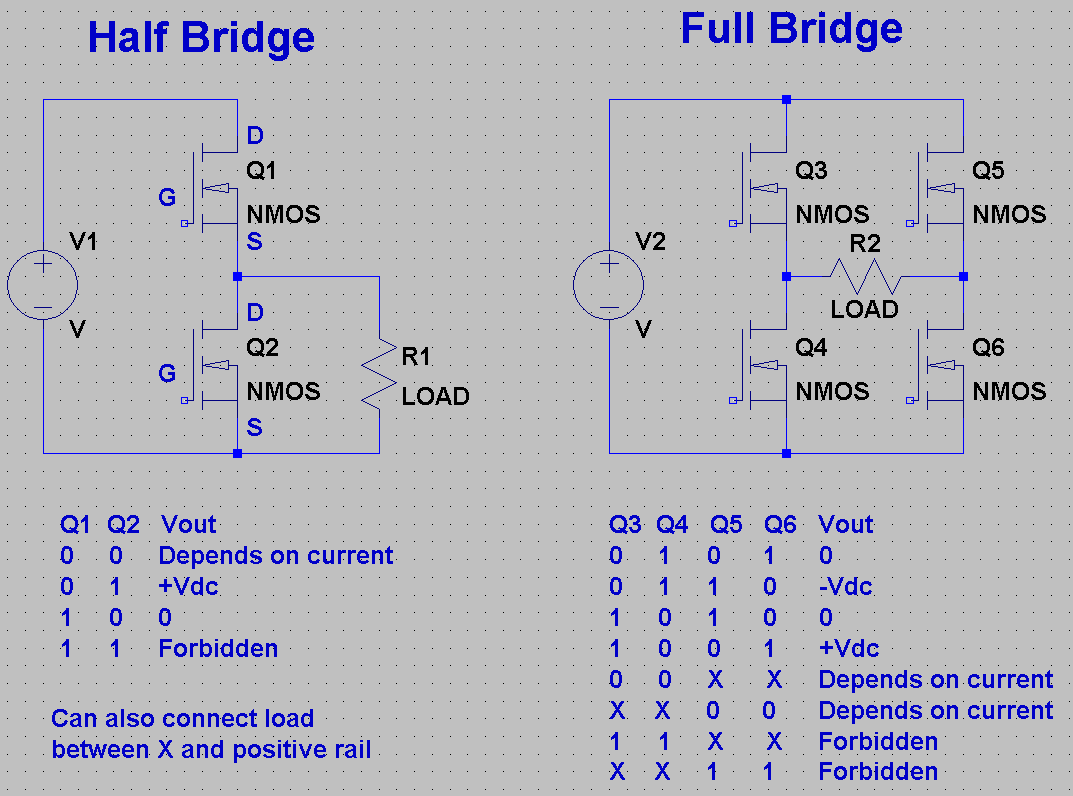
 So the total on and off losses in Q1 are approximately 5.6 uJ. We can improve the situation, more on that later.
So the total on and off losses in Q1 are approximately 5.6 uJ. We can improve the situation, more on that later.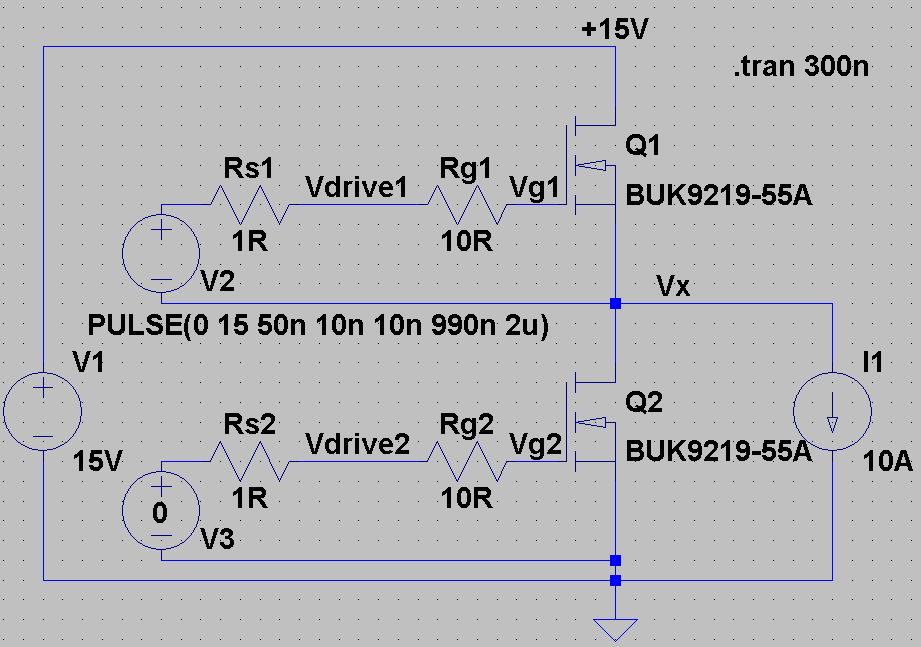
 Turn on of Q1: 3.5 uJ
Turn on of Q1: 3.5 uJ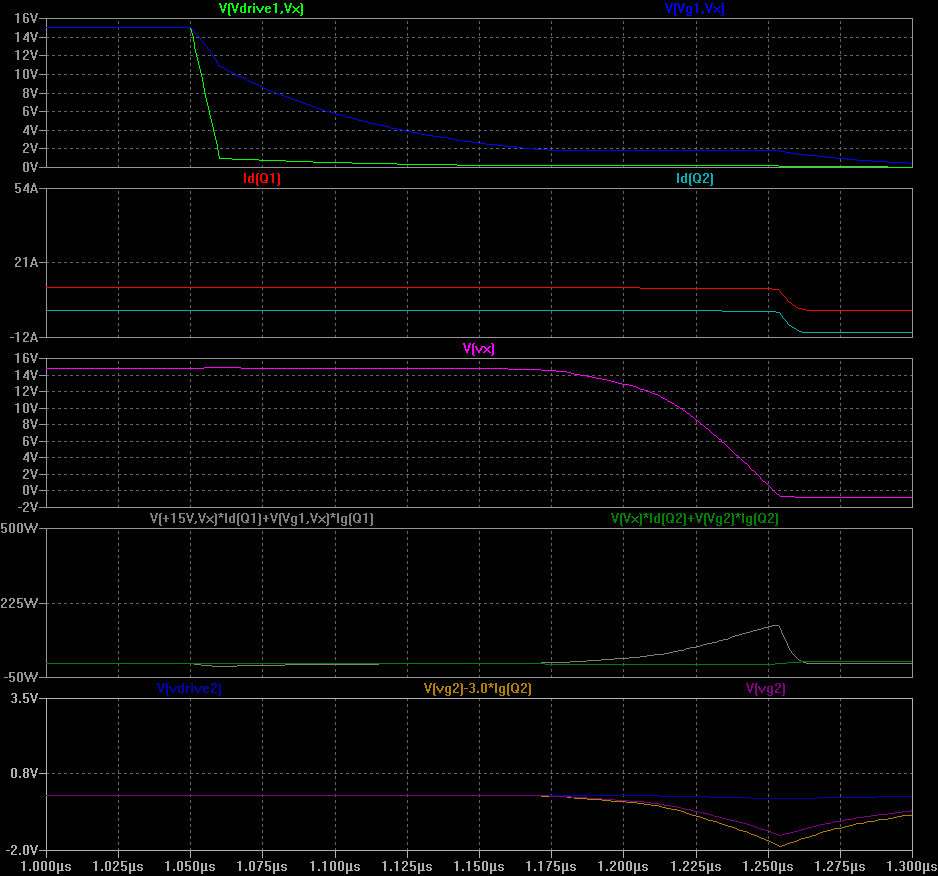
 Turn on of Q1: 1.2 uJ
Turn on of Q1: 1.2 uJ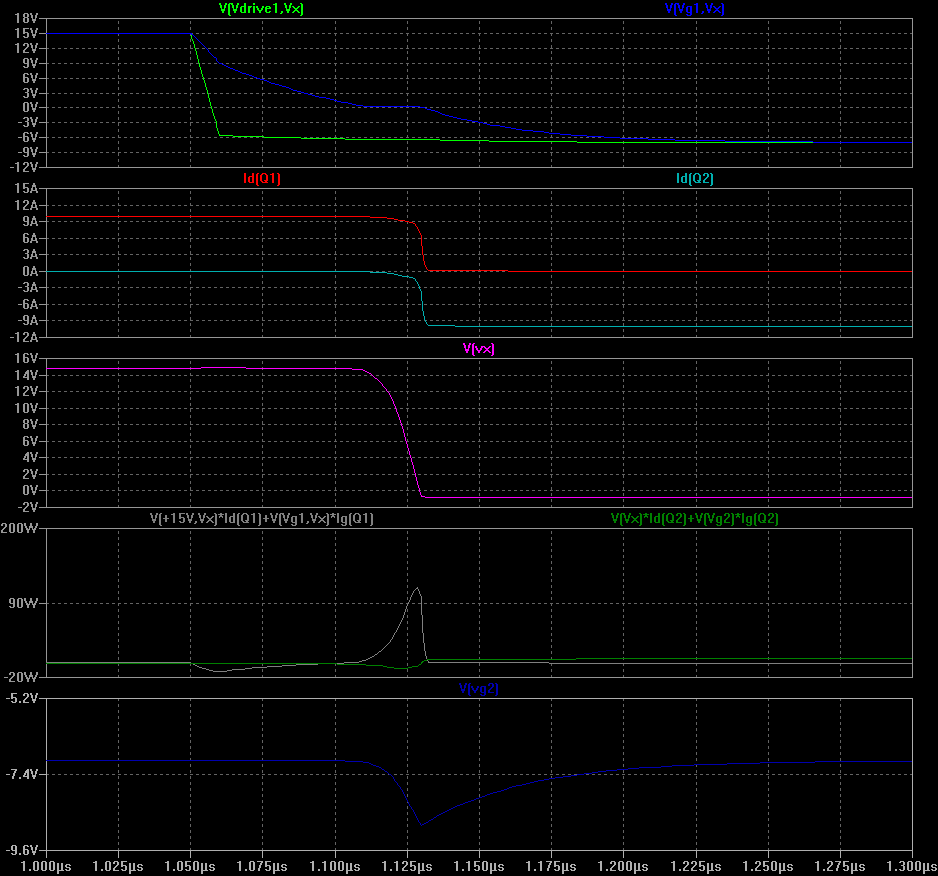
 Turn on of Q1: 2.7 uJ
Turn on of Q1: 2.7 uJ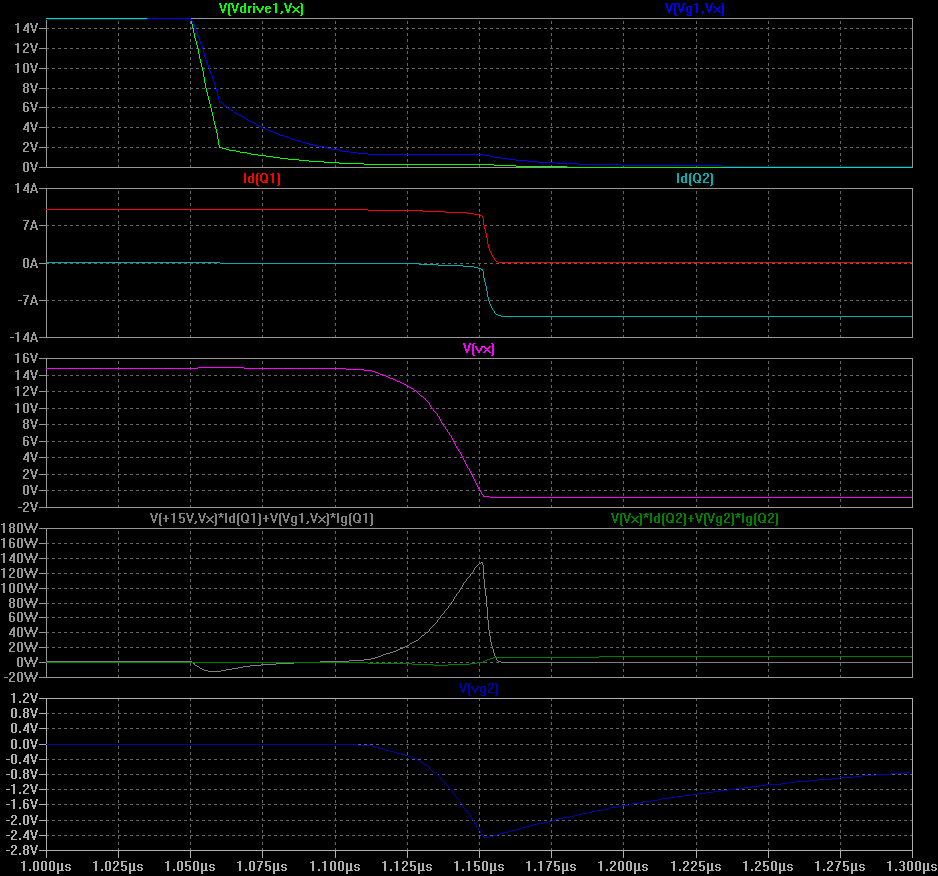 Turn off of Q2: 2.2 uJ
Turn off of Q2: 2.2 uJ We now have an extra degree of freedom to play with: the current through the feedback windings If. With a bit of closed loop control, we can adjust If such that:
We now have an extra degree of freedom to play with: the current through the feedback windings If. With a bit of closed loop control, we can adjust If such that:
 We see that:
We see that: Well, after a few ms of transient behaviour at startup, we do get a sinusoidal current out. However, we have quite a bit of phase shift (power measurements using this would be useless!). In a future post we will talk about bandwidth extension with a third ferrite core functioning as a current transformer.
Well, after a few ms of transient behaviour at startup, we do get a sinusoidal current out. However, we have quite a bit of phase shift (power measurements using this would be useless!). In a future post we will talk about bandwidth extension with a third ferrite core functioning as a current transformer. But we can compensate for it. We can do this by adding an opposing EMF to the circuit. A good way to do this is to add a second fluxgate with opposite 'polarity' to the first as shown:
But we can compensate for it. We can do this by adding an opposing EMF to the circuit. A good way to do this is to add a second fluxgate with opposite 'polarity' to the first as shown: We now have a vastly reduced Ep term - theoretically zero (we will have a look at component tolerances later). Also, we now have the opportunity to measure the difference between Vm1 and Vm2, which we see is (in principle) zero Volts at zero primary current:
We now have a vastly reduced Ep term - theoretically zero (we will have a look at component tolerances later). Also, we now have the opportunity to measure the difference between Vm1 and Vm2, which we see is (in principle) zero Volts at zero primary current: And if we have a 1A primary current Ip, we get some nonzero quantites: the voltage between Vm1 and Vm2 is nonzero and Ep is nonzero.
And if we have a 1A primary current Ip, we get some nonzero quantites: the voltage between Vm1 and Vm2 is nonzero and Ep is nonzero. If we sweep Ip over a -3A to +3A range (this is the X axis), and look at the average of Vx (i.e. output of a low pass filter) and the RMS value of Ep, things look pretty good:
If we sweep Ip over a -3A to +3A range (this is the X axis), and look at the average of Vx (i.e. output of a low pass filter) and the RMS value of Ep, things look pretty good: Our current to voltage gain has doubled, and Ep is vastly reduced compared to the original 320 mV RMS. In fact, it should go to zero when Ip = 0 (note that component tolerances are not yet considered). So, we have gotten both more output signal and less voltage injection into the primary circuit, which is most welcome.
Our current to voltage gain has doubled, and Ep is vastly reduced compared to the original 320 mV RMS. In fact, it should go to zero when Ip = 0 (note that component tolerances are not yet considered). So, we have gotten both more output signal and less voltage injection into the primary circuit, which is most welcome. Oh ****. Our sensor is nice and linear in the -3A to +3A range, but all kinds of nonlinear outside that (not sure what the glitch around +12A is, but I don't like it). This is not going to work as desired.
Oh ****. Our sensor is nice and linear in the -3A to +3A range, but all kinds of nonlinear outside that (not sure what the glitch around +12A is, but I don't like it). This is not going to work as desired. V2 provides the excitation square wave.
V2 provides the excitation square wave.
 By adding some .measure commands to the Spice file, we can plot the average (i.e. DC component) of Vx against the applied Ip. This averaging can be implemented using a simple low pass filter. We are now getting something like 1 V / A gain - excellent.
By adding some .measure commands to the Spice file, we can plot the average (i.e. DC component) of Vx against the applied Ip. This averaging can be implemented using a simple low pass filter. We are now getting something like 1 V / A gain - excellent. 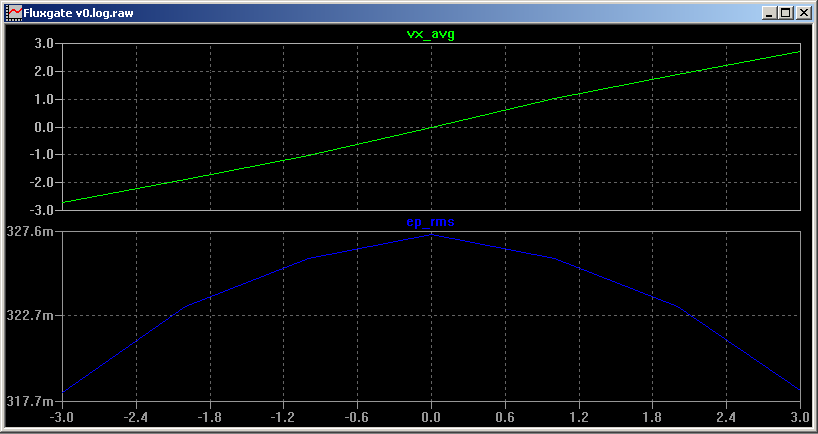 Next time we will look at a double core fluxgate to show how we can reduce Ep significantly.
Next time we will look at a double core fluxgate to show how we can reduce Ep significantly.