As Zach teased on the touch slider update, there's been work happening behind the scenes to implement the Izhikevich neuron model on the newer NeuroBytes boards. Well I may as well introduce myself (hi, I'm Patrick! In the daytime I'm an Electrical Engineer, and have been attracted to help out the project here because it reminds me of Valentino Braitenberg's Vehicles, a book that helped kick-start my interest in robotics) and I figured I would keep a log during my work for any budding programmers who would want a peek into the work of an embedded software engineer.

Straight from the source, we have a model of the neuron where

v' = 0.04v**2 + 5v + 140 - u + I
u' = a(bv - u)
if v >= 30, then {v = c, u = u + d}

which I implemented in C on my host machine as

#include <stdint.h>
#include <stdio.h>

typedef float float_t;

typedef struct {
    float_t a, b, c, d;
    float_t potential, recovery;
} fneuron_t;

static void RS(fneuron_t *neuron) {
    // create a "regular spiking" floating point neuron
    neuron->a = 0.02;
    neuron->b = 0.2;
    neuron->c = -65;
    neuron->d = 2;
    neuron->potential = neuron->recovery = 0;
}

static void step_f(fneuron_t *neuron, float_t synapse, float_t ms) {
    // step a neuron through ms milliseconds with synapse input
    //   if you don't have a good reason to do otherwise, keep ms between 0.1
    //   and 1.0
    if (neuron->potential >= 30) {
        neuron->potential = neuron->c;
        neuron->recovery += neuron->d;
        return;
    }
    float_t v = neuron->potential;
    float_t u = neuron->recovery;
    neuron->potential = v + ms * (0.04 * v * v + 5 * v + 140 - u + synapse);
    neuron->recovery = u + ms * (neuron->a * (neuron->b * v - u));
    return;
}

int main(void) {
    fneuron_t spiky;
    RS(&spiky);
    for (int i = 0; i < 2000; i++) {
        if (i < 100) {
            step_f(&spiky, 0, 0.1);
        } else {
            step_f(&spiky, 10, 0.1);
        }
        printf("%f %f\n", i * 0.1, spiky.potential);
    }
}

I compile and run this with

gcc izhi.c -o izhi
./izhi > rs.dat

I use gnuplot to display this quickly, by starting it up and using the command

plot 'rs.dat' with lines

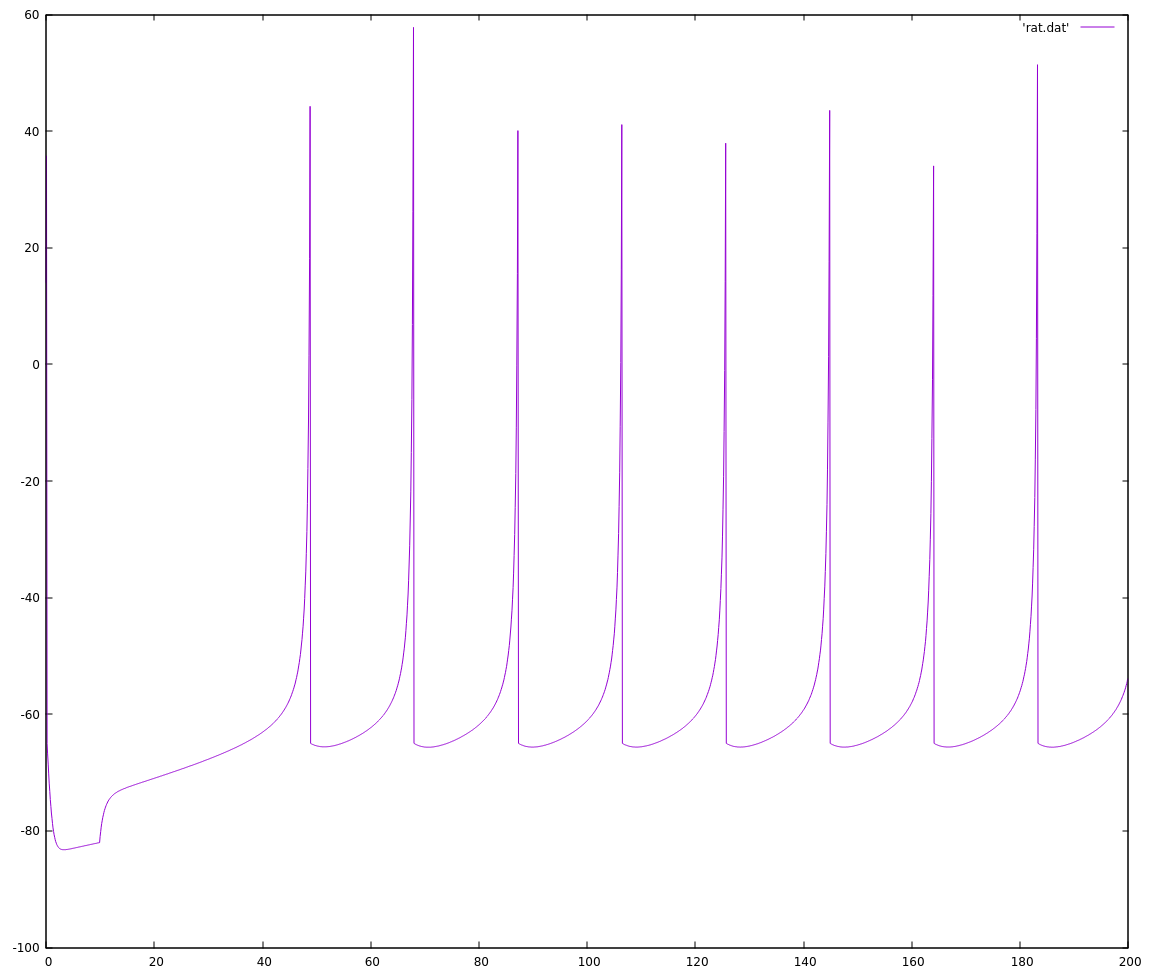
The next step was to implement the easiest fixed-point version I can think of, to see how well its output aligns with the floating-point version. The reason to do this is that floats mask a lot of complexity (their dynamic range protects me from rounding errors, overflow, and underflow, for example) that will become my problem to deal with when I work with fixed point arithmetic. Here is the added fixed-point math and an updated main function:

typedef int16_t fixed_t;
#define FSCALE 320

typedef struct {
    // using 1/a, 1/b because a and b are small fractions
    fixed_t a_inv, b_inv, c, d;
    fixed_t potential, recovery;
} ineuron_t;

static void RS_i(ineuron_t *neuron) {
    neuron->a_inv = 50;
    neuron->b_inv = 5;
    neuron->c = -65 * FSCALE;
    neuron->d = 2 * FSCALE;
    neuron->potential = neuron->recovery = 0;
}

static void step_i(ineuron_t *neuron, fixed_t synapse, fixed_t fracms) {
    // step a neuron by 1/fracms milliseconds. synapse input must be scaled
    //  before being passed to this function.
    if (neuron->potential >= 30 * FSCALE) {
        neuron->potential = neuron->c;
        neuron->recovery += neuron->d;
        return;
    }
    fixed_t v = neuron->potential;
    fixed_t u = neuron->recovery;
    neuron->potential = v + ((v * v) / FSCALE / 25 + 5 * v
                             + 140 * FSCALE - u + synapse) / fracms;
    neuron->recovery = u + ((v / neuron->b_inv - u) / neuron->a_inv) / fracms;
    return;
}

int main(void) {
    fneuron_t spiky_f;
    ineuron_t spiky_i;
    RS_f(&spiky_f);
    RS_i(&spiky_i);
    for (int i = 0; i < 5000; i++) {
        if (i < 100) {
            step_f(&spiky_f, 0, 0.1);
            step_i(&spiky_i, 0, 10);
        } else {
            step_f(&spiky_f, 10, 0.1);
            step_i(&spiky_i, 10 * FSCALE, 10);
        }
        printf("%f %f %f\n", i * 0.1, spiky_f.potential,
               (float_t)(spiky_i.potential) / FSCALE);
    }
}

I'd like to highlight a few habits that usually make my life easier:

typedef int16_t fixed_t;
#define FSCALE 320

I took an initial guess that I'd be using 16-bit ints (this eventually will target a 32bit processor, but Zach's earlier work was happily using 16 bits, so I'm starting there), but if I change my mind later I don't want to track down every place that I declared an int16_t and change it to an int32_t. That's setting myself up for a mistake and a frustrating bug, so I use the typedef to "create" a new type, aliased to int16_t, that I can use all over and only need to change one line to switch it all to a different size.

Similarly, I #define'd the scaling factor right there as well. This number is equivalent to 1.0 in the floating point implementation, and again if I find my scaling is wrong, I can just change it in this one place instead of tracking down every usage. I chose 320 because a 16bit signed int goes from -2^15 to +2^15, or roughly speaking -32000 to +32000, and the neuron potential and recovery values stay comfortably within the -100 to +100 range. There's definitely value in analyzing this decision more thoroughly; if I'm too cautious then I'm losing precision by never exercising the full range, but if I'm not cautious enough I risk overflowing the variable size and "wrapping around" from larger than the largest possible positive value to a very large negative value, or vice-versa.

Lastly, I kept the floating point implementation around so that I can run my new fixed point version against the same inputs and compare the two side-by-side to make it easier to spot any differences in behaviour. And it's a good thing I did, because if I build and run this version and examine the output,

gcc izhi.c -o izhi && ./izhi >rs.dat && gnuplot
gnuplot> plot 'rs.dat' using 1:2 title 'floating' with lines, \
              'rs.dat' using 1:3 title 'fixed' with lines

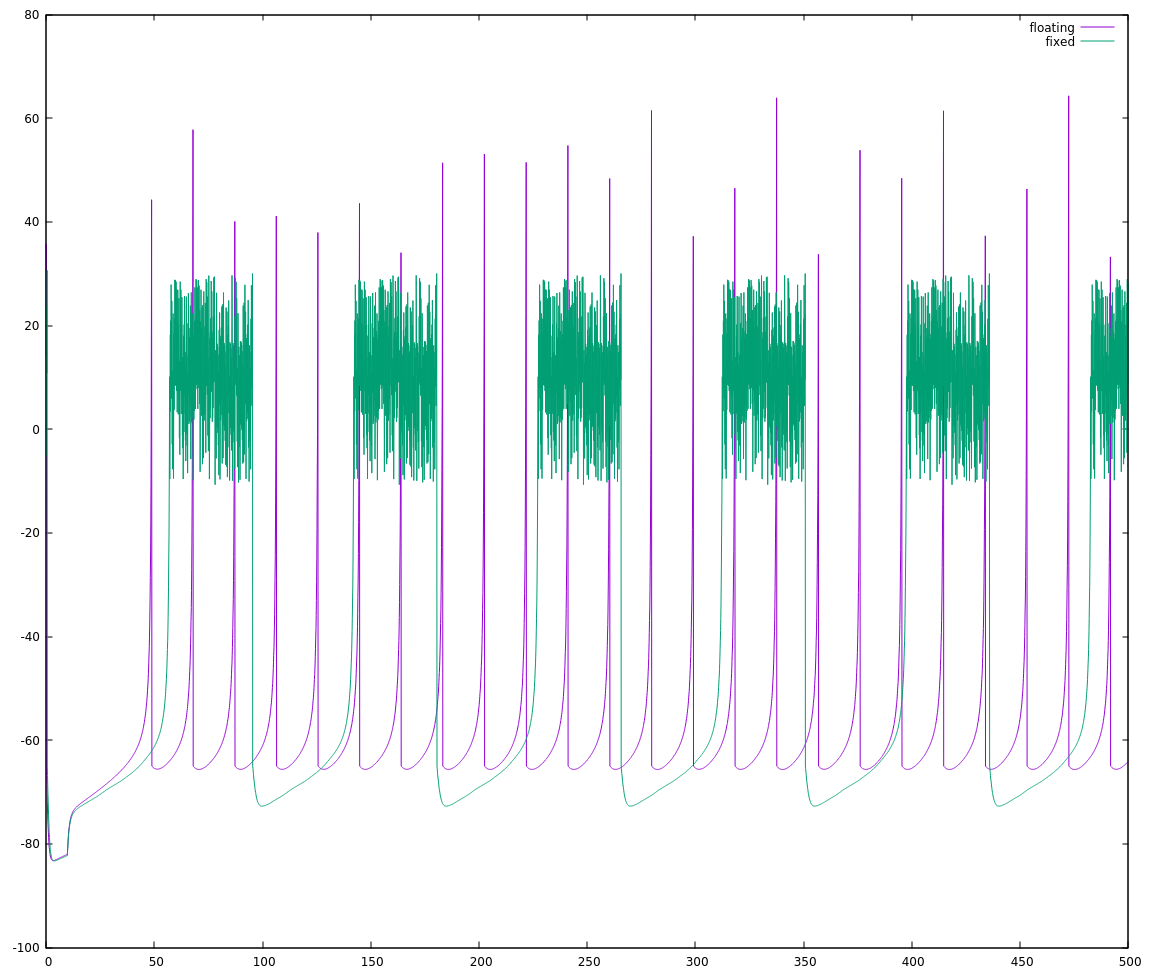
I get this:

If I weren't comparing the two on the same plot, I'd be tempted to say they're basically the same. Side-by-side though, we can immediately see that one is running slightly faster than the other. If we count the spikes starting with the nearly-coincident ones near t=200 until the next nearly-coincident ones (roughly t = 375), there are 10 floating point spikes vs. 9 fixed point spikes. The fixed point implementation is rising approximately 90% as fast as the floating point implementation I'm considering my reference.

This is why I started with the simplest attempt I thought would work. If I saw this mis-alignment with a more clever attempt, I'd start asking myself where my cleverness let me down and I'd have many more dark corners to go looking in. As it stands, it's fairly simple to look through the code and see if I missed something. There's maybe a half-dozen places to make sure I did the (a*x -> x/(1/a)) conversion properly, and I can convince myself that I did it right.

It looked like I had converted the numbers properly, so I started looking for another explanation, something specific to how I was doing the fixed point math. The fixed point neuron seems to rise a little bit slower than the floating point one, so I thought maybe I had a small error in my math that on any one step would be inconsequential, but over hundreds of steps would add up.

When you divide integers in C, the computer doesn't necessarily round the result up or down to the nearest integer, it will just truncate it and throw away the lost precision. This means that every number between 50 and 59, when divided by 10, will return 5. This is one way to have a constant bias on your results, and the way I know to deal with this is to add half of your divisor to the numerator before doing the division. (50 + 5)/10 = 5, (54 + 5)/10 = 5, but (55 + 5)/10 = 6.

I tried applying this trick, and it didn't really help. In fact, as a first step I split out `((v * v) / FSCALE / 25 + 5 * v + 140 * FSCALE - u + synapse)` into a partial result, and the whole calculation went sideways and `neuron->potential` would just oscillate really quickly in between -20 and 0. I think the math in that equation was all being done in 32 (or 64) bit integers that are the native type on my computer and only being re-cast to 16 bits at the end. Forcing the partial result in to a 16 bit int exposed an integer overflow that wasn't obvious otherwise.

Checking this guess was pretty easy, I changed to `typedef int32_t fixed_t;` and the result was back to well-behaved spikes (but still activating at a slower-then-expected rate). Okay sure, my guess of `#define FSCALE 320` must have been a little too high, so I cut it down a bit and ran with

typedef int16_t fixed_t;
#define FSCALE 160

Aaaand... oh dear. That hasn't exactly helped.

It seems I was just lucky with my first choice for scaling, and there's actually a lot of choices that would not work (reducing the scale should be safe, so long as the lost precision doesn't destroy the behaviour). It's time to stop shooting from the hip on this one, and go back to proper analysis.

My initial thought on the scaling was that the neuron potential stayed well within the -100..100 range, so I could safely use that as my min and max values. Looking at the equations as I've written them out, that's clearly wrong for partial results. Just starting with the squaring term and substituting our assumed max for v:

v * v => (100 * FSCALE) * (100 * FSCALE)
      => 10000 * FSCALE * FSCALE

Whoops. Even if we were to restrict v to 30, we'd be at (900 * FSCALE**2), well past our assumed max of 100, and I already know that's not an assumption I can make, because v actually resets all the way down at -65. Luckily, we can re-order the operations: the next thing I do with this squared result is divide it, so I can keep everything more in check by distributing that division inside the squaring.

partial = (v * v) / FSCALE / 25

becomes

partial = ((v / (SQRT_FSCALE * 5)) * (v / (SQRT_FSCALE * 5)))

where `SQRT_FSCALE` is the square root of `FSCALE`. Checking now to see how likely it is we overflow by calculating the first part of that partial while substituting 100 for v:

((100 * FSCALE) / (SQRT_FSCALE * 5))
 ==> ((100 / 5) * (FSCALE / SQRT_FSCALE)) 
 ==> (20 * SQRT_FSCALE)

and we can see that squaring that term will give us a max value of `partial = 400 * FSCALE`. Much more reasonable.

Of course, the next two terms we add are `5 * v + 140 * FSCALE`, which would max out at `5 * (100 * FSCALE) + 140 * FSCALE == 640 * FSCALE`.

Turning our attention to the neuron recovery variable, u, even with ridiculously large values of v = 100 and u = -100, the step size is 2.2, so I don't see it contributing much (`2.2 * FSCALE` that is) here. Similarly, for now the value of `synapse` I'm using is `10 * FSCALE`, so combined they are on the order of 1% the max contribution of the first three terms.

So I can choose `FSCALE` as roughly `INT_MAX / 1100` and try again. This could be 29.789, but I need to round down (integers!) to 29, and then there's an additional restriction that I need `SQRT_FSCALE` as well, so may as well cut back to `FSCALE = 25; SQRT_FSCALE = 5;`. Trying that, I get:

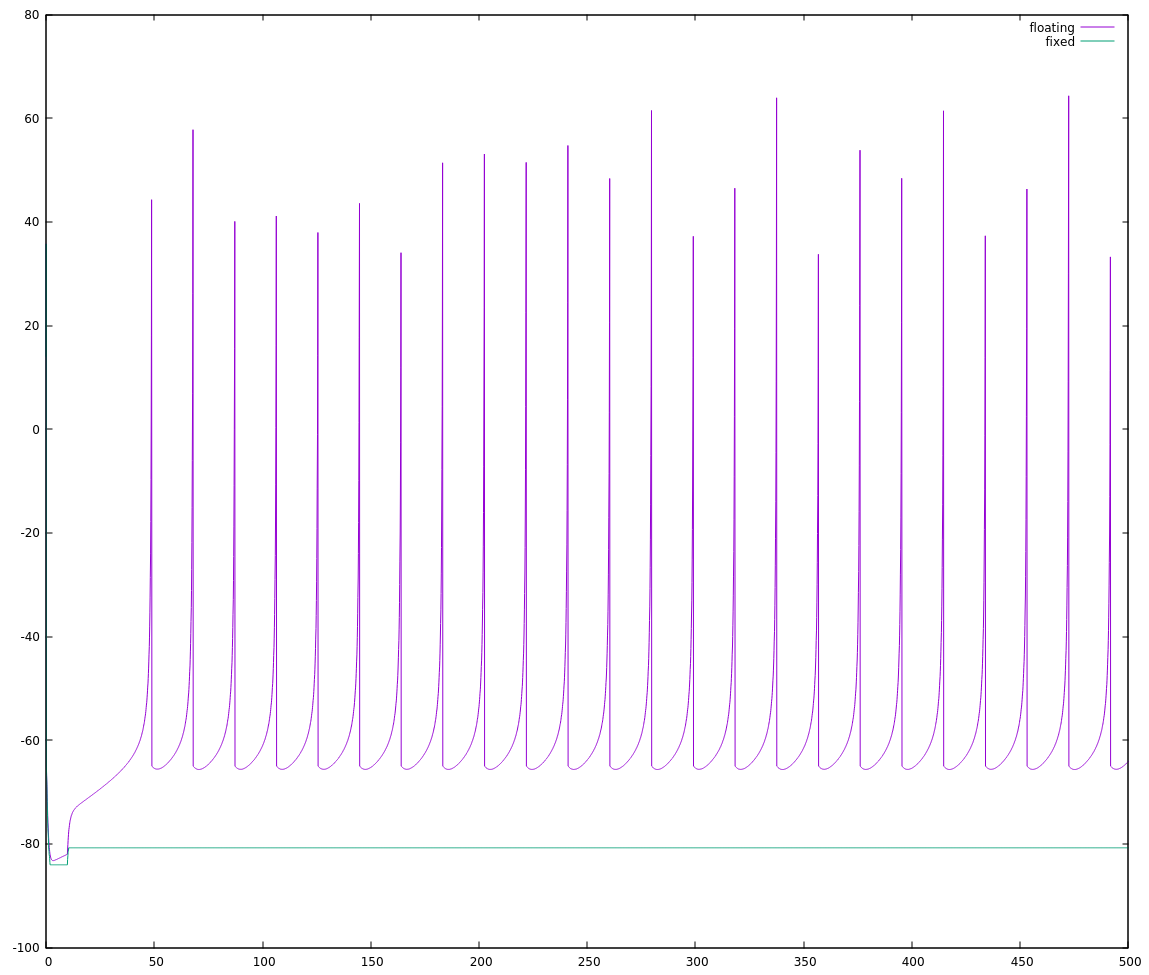
Okay, not exactly stellar either. Zooming in to the start of this run:

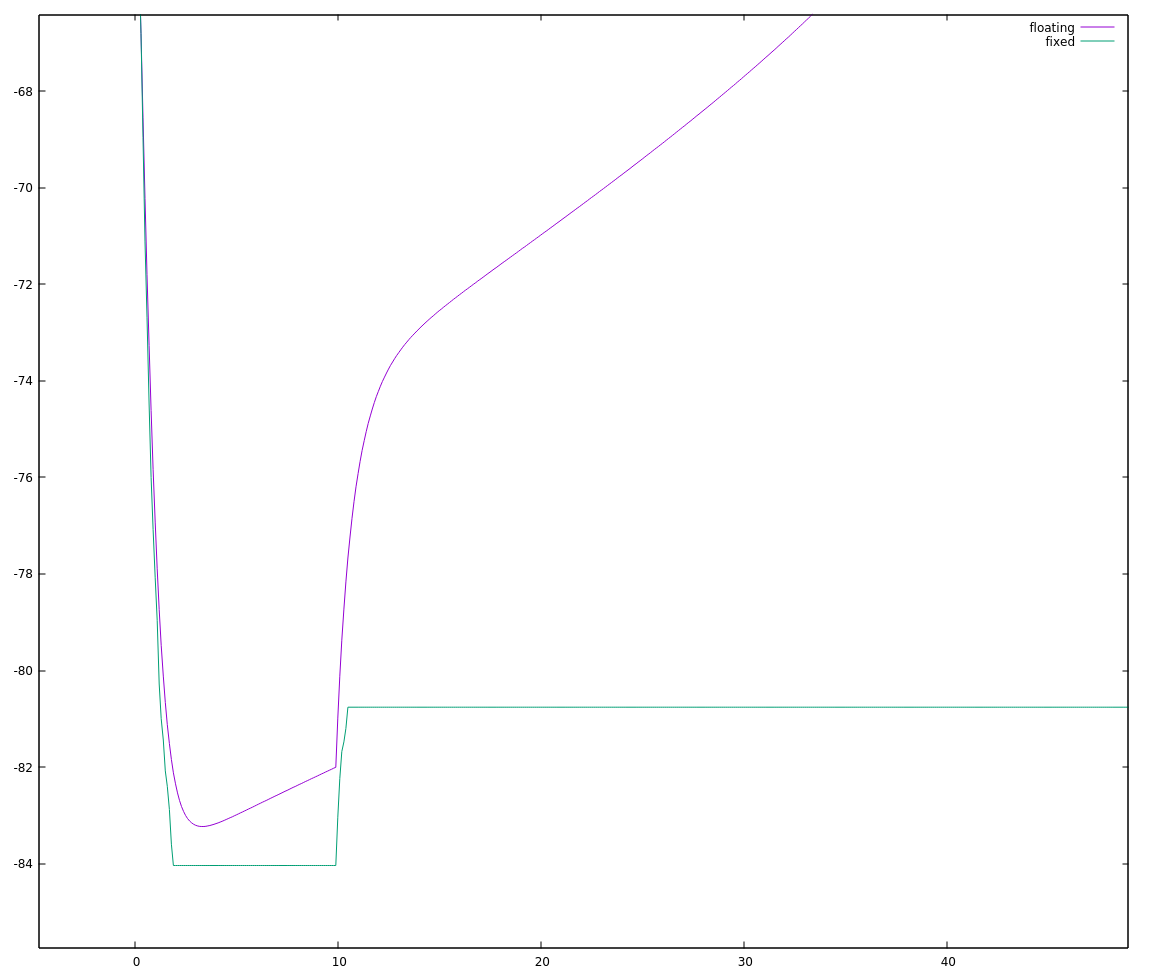
the fixed point implementation looks "choppy", which seems typical of too little precision to me.

I've broken out the calculation for neuron potential as

// neuron->potential = v + ((v * v) / FSCALE / 25 + 5 * v
//                          + 140 * FSCALE - u + synapse) / fracms;
fixed_t partial = ((v / (SQRT_FSCALE * 5)) * (v / (SQRT_FSCALE * 5)));
neuron->potential = v + (partial + 5 * v + 140 * FSCALE - u + synapse) / fracms;

and if I want to bring down the max value of sub-calculations of the potential, I need to reduce the size of the partial, 5*v, and 140*FSCALE terms. Luckily, they're all divided by fracms, which I can just distribute inside the parentheses. Unfortunately, partial is already pretty large and needs to be stored somewhere as a fixed_t, so the best approach seems to be either I apply the divisor to only one of the subpartials (and suffer a loss of precision), or I need a divisor I can break in to two terms and apply to each. For now, I'm going to lock down a fracms of 10, and see how that shakes out. This is a hit on the flexibility of the step_i() function, but we need to get it working correctly first.

fixed_t subpartial = v / (SQRT_FSCALE * 5);
fixed_t partial = ((subpartial / 5) * (subpartial / 2) + v / 2
                   + 14 * FSCALE) + (synapse - u) / 10;
neuron->potential = v + partial;

Now partial will be on the order of

(400 * FSCALE / 10) + 100 * FSCALE / 2 + 14 * FSCALE == 104 * FSCALE

actually much closer to our original (100 * FSCALE) limit. Choosing a value for FSCALE using 32768/104 = 315.077, the nearest perfect square without going over is 289 (17**2). This gave a more promising, but not perfect waveform:

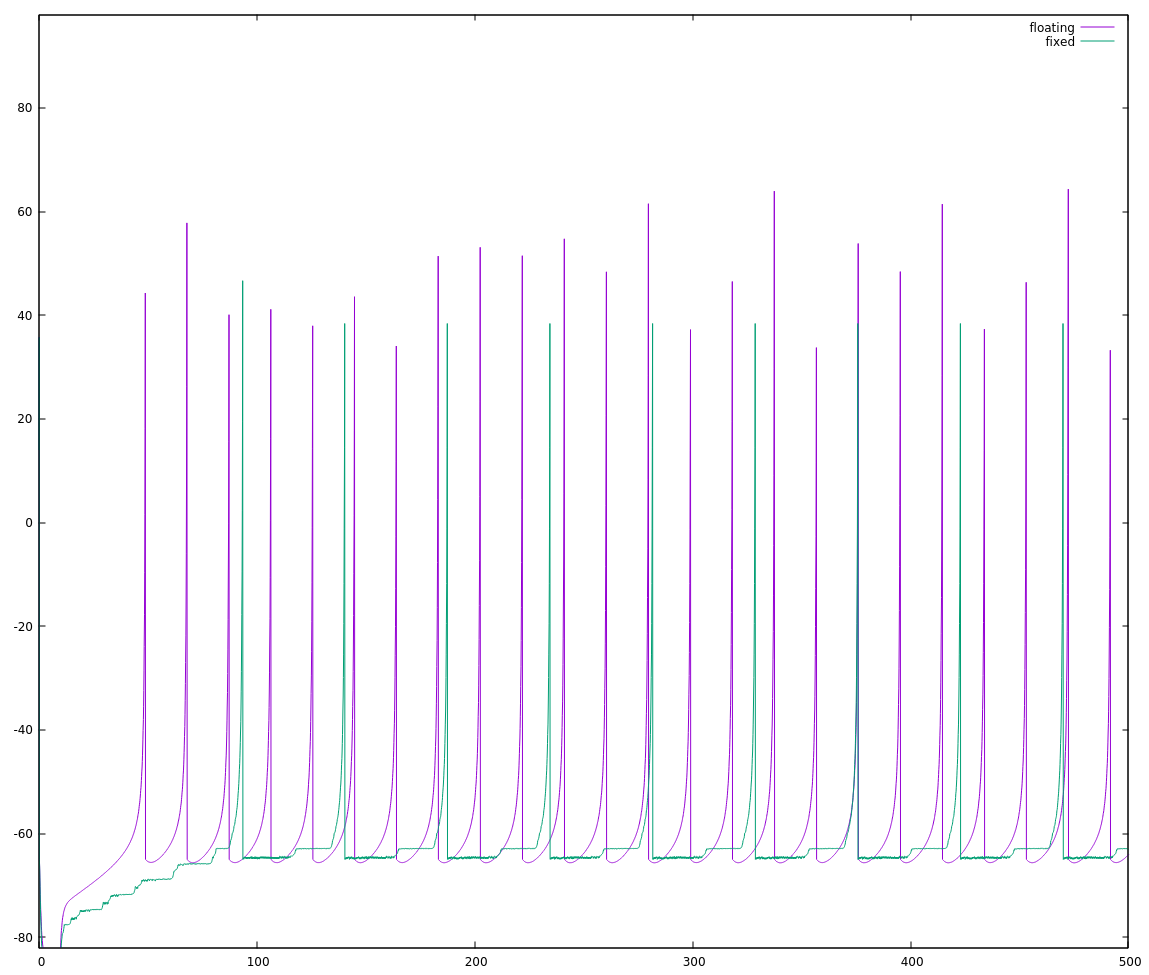
Actually, zooming in I can see distinct steps in the neuron potential which makes me suspect a loss of precision:

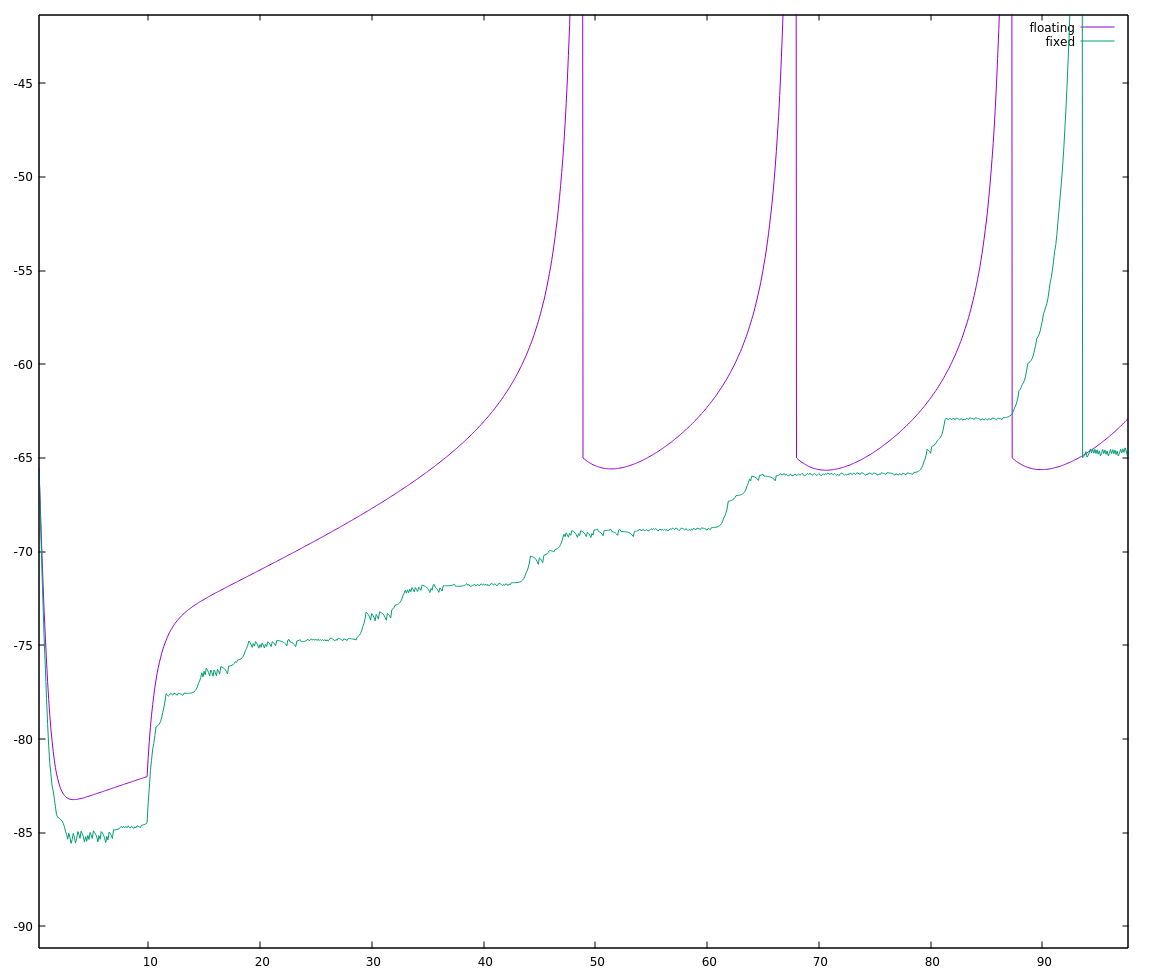
and plotting out the value of `neuron->recovery` shows I very distinctive break from the floating point behaviour:

I looked at a few different choices for FSCALE and juggled the distribution of divisors around a little bit, and I suspect that 16 bit signed ints are just a little shy of the dynamic range needed to implement this algorithm in a straightforward manner. So I'm going to do something I should've done a long time ago: I'll move to 32 bit ints.

INT_MAX on an int32_t is roughly 2 billion, so we'll set a conservative FSCALE of 1 million. Yes, that made things much much easier:

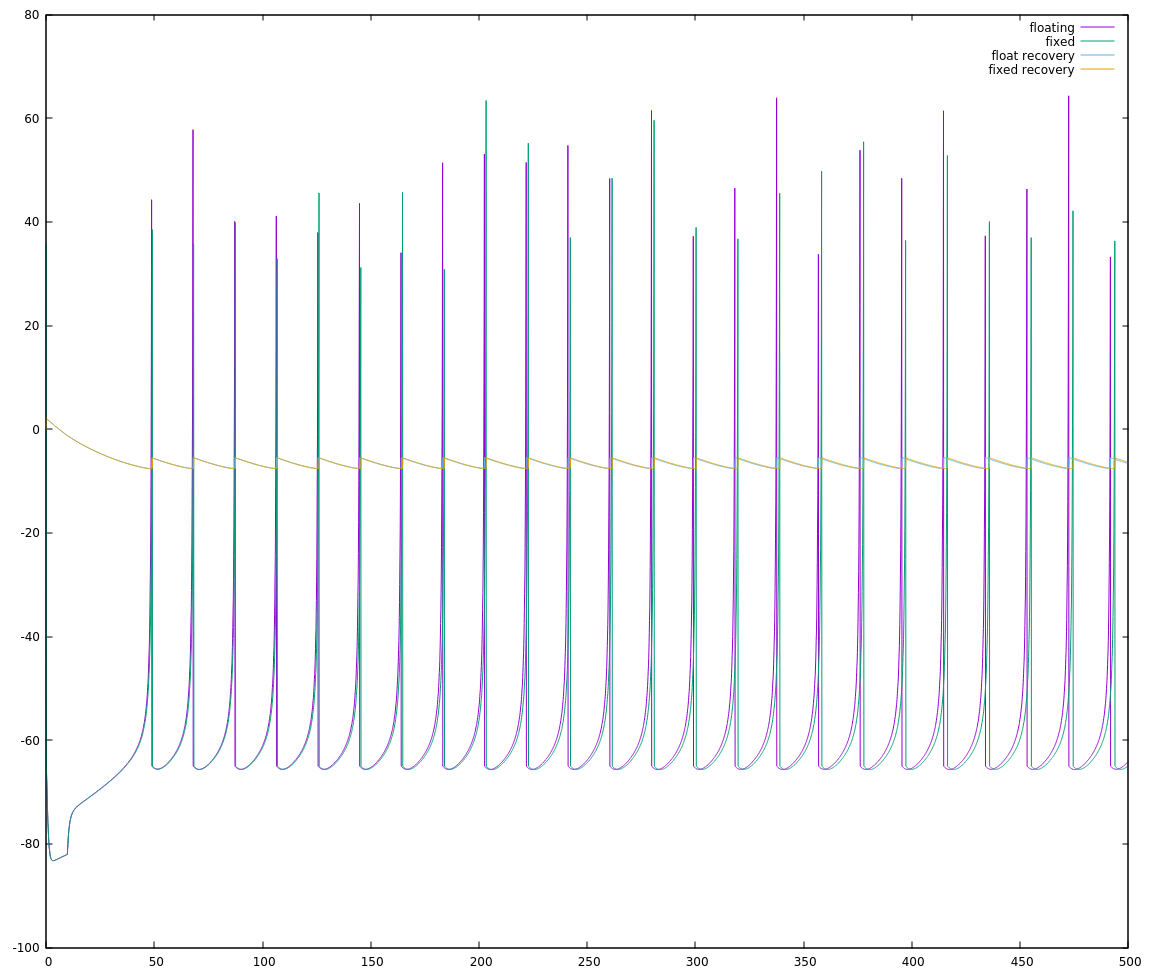The final code at this point, working with 32bit ints on my personal computer follows. In my next log, I'll go through what it took me to get this running on my NeuroByte board and then how to get it running more quickly.

#include <stdint.h>
#include <stdio.h>

typedef float float_t;

typedef struct {
    float_t a, b, c, d;
    float_t potential, recovery;
} fneuron_t;

static void RS_f(fneuron_t *neuron) {
    // create a "regular spiking" floating point neuron
    neuron->a = 0.02;
    neuron->b = 0.2;
    neuron->c = -65;
    neuron->d = 2;
    neuron->potential = neuron->recovery = 0;
}

static void step_f(fneuron_t *neuron, float_t synapse, float_t ms) {
    // step a neuron through ms milliseconds with synapse input
    //   if you don't have a good reason to do otherwise, keep ms between 0.1
    //   and 1.0
    if (neuron->potential >= 30) {
        neuron->potential = neuron->c;
        neuron->recovery += neuron->d;
        return;
    }
    float_t v = neuron->potential;
    float_t u = neuron->recovery;
    neuron->potential = v + ms * (0.04 * v * v + 5 * v + 140 - u + synapse);
    neuron->recovery = u + ms * (neuron->a * (neuron->b * v - u));
    return;
}

typedef int32_t fixed_t;
#define SQRT_FSCALE 1000
#define FSCALE (SQRT_FSCALE * SQRT_FSCALE)

typedef struct {
    // using 1/a, 1/b because a and b are small fractions
    fixed_t a_inv, b_inv, c, d;
    fixed_t potential, recovery;
} ineuron_t;

static void RS_i(ineuron_t *neuron) {
    neuron->a_inv = 50;
    neuron->b_inv = 5;
    neuron->c = -65 * FSCALE;
    neuron->d = 2 * FSCALE;
    neuron->potential = neuron->recovery = 0;
}

static void step_i(ineuron_t *neuron, fixed_t synapse, fixed_t fracms) {
    // step a neuron by 1/fracms milliseconds. synapse input must be scaled
    //  before being passed to this function.
    if (neuron->potential >= 30 * FSCALE) {
        neuron->potential = neuron->c;
        neuron->recovery += neuron->d;
        return;
    }
    fixed_t v = neuron->potential;
    fixed_t u = neuron->recovery;
    fixed_t partial = (v / SQRT_FSCALE) /  5;
    neuron->potential = v + (partial * partial + 5 * v  + 140 * FSCALE
                             - u + synapse) / fracms;
    neuron->recovery = u + ((v / neuron->b_inv - u) / neuron->a_inv) / fracms;
    return;
}

int main(void) {
    fneuron_t spiky_f;
    ineuron_t spiky_i;
    RS_f(&spiky_f);
    RS_i(&spiky_i);
    for (int i = 0; i < 5000; i++) {
        if (i < 100) {
            step_f(&spiky_f, 0, 0.1);
            step_i(&spiky_i, 0, 10);
        } else {
            step_f(&spiky_f, 10, 0.1);
            step_i(&spiky_i, 10 * FSCALE, 10);
        }
        printf("%f %f %f %f %f\n", i * 0.1, spiky_f.potential,
               (float_t)(spiky_i.potential) / FSCALE,
               spiky_f.recovery, (float_t)(spiky_i.recovery) / FSCALE);
    }
}

PS: If I were doing this work professionally, I would have been expected to try the 32bit integers first. The chip this is eventually targetting is a 32bit core, and can do 32bit multiplication in a single clock cycle. Even if it couldn't, I should be trying the easy thing first, and only spending my time optimizing some code if I can show it actually needs to be faster. It's often the case that code runs much differently than one expects, especially on an architecture one isn't intimately familiar with.

Even so, I've got more ideas for a 16bit version, so I may just come back to it later.