The unusual geometry of plotbot means that one has to find a way to map the Cartesian coordinates of what shall be drawn to the coordinates of the steppers in a way that the tip of the triangle that is formed by the arms will follow the Cartesian coordinates of the drawing. In the first Log I made a python script that shows how to do that transformation if you want to go from stepper coordinates to drawing/tip coordinates. But to drive the steppers one has to calculate the transformation the other way around, which has given me some headaches but in the following I'll show how I solved that problem.

First some definitions:

• x and y denote coordinates in tip/drawing space, meaning x and y are the coordinates of a point in the plane of the drawing

• a and b denote coordinates in stepper space, meaning that a and b are coordinates in a hypothetical plane which is defined by the steps of the stepper motors, but they can easily be expressed in tip space:

With d being the distance between the rails.

I could not  figure out how to go the reverse way from what I did in the first Log but there is another way to calculate the tip position from the stepper coordinates:

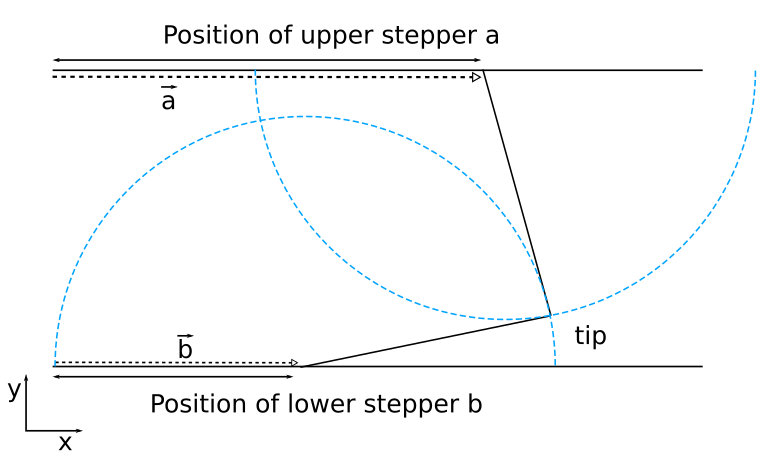
So if we want to calculate the position of the tip we can simply calculate the position of the tip we can simply calculate the intersections of the the two circles centered at position (a, d) and (b, 0) with a radius that equals the length of the arms and choose the rightmost intersection as the solution.

Now this is easily reversed:

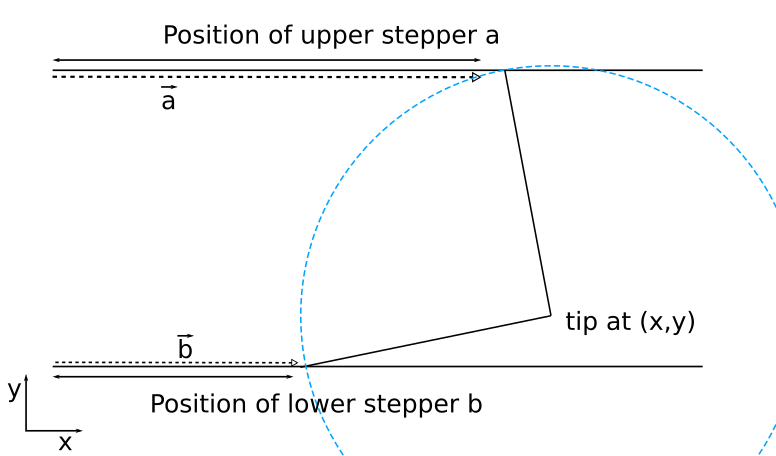
If we know the position of the tip (x,y) we can calculate the intersections of the circle centered at (x,y) with a radius that equals the length of the arms and the lines defined by the upper and lower rail. Now we choose the leftmost solutions and have our coordinates a and b, that define a point in stepper space (a,b).

So that is pretty neat, but there is one more thing to know: These transformations are far from linear, that means they can't be reproduced just by a set of simple translations, rotations or a squeezing/unsqueezing of the length-scales.

This haunted me while programming the control-software, and I will show the implications of this in a later log.