Project Stages
- The mathematics:
- Calculating modified Julian Day number (JD)
- Calculating Greenwich Mean Sidereal Time (GMST)
- Calculating Universal Time
- Calculating the Right Ascension (RA) and Declination (Dec) of the Sun.
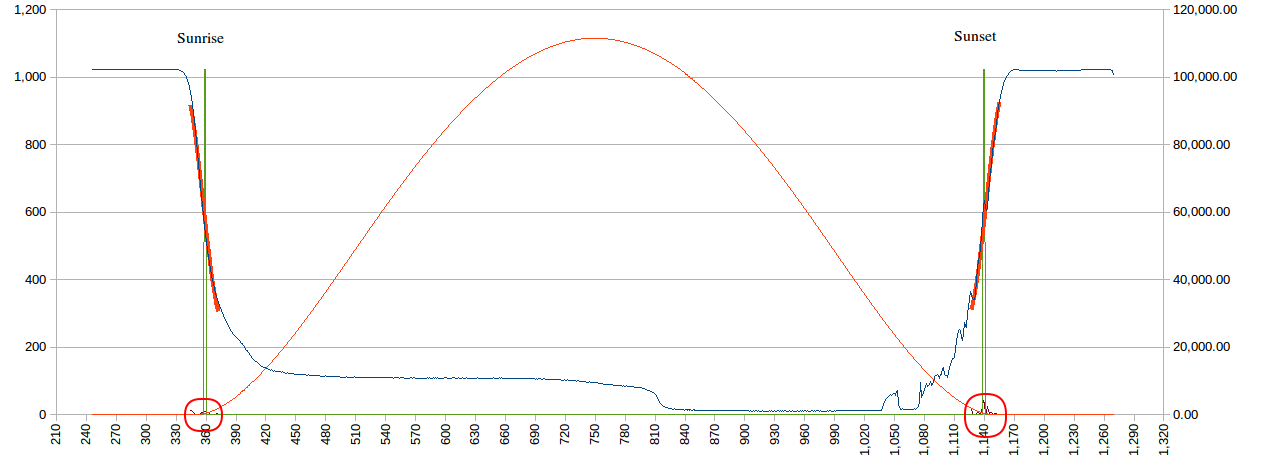
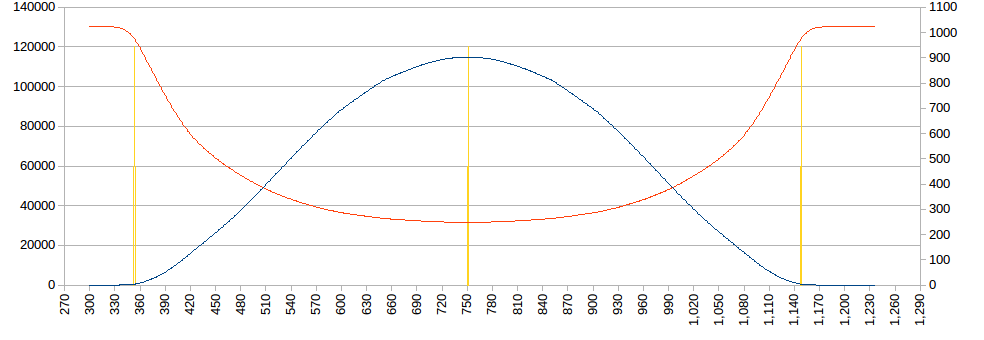
- Calculating sun rise and sun set or any other position of the sun.
- Calculating your Longitude based on sun rise and sun set times.
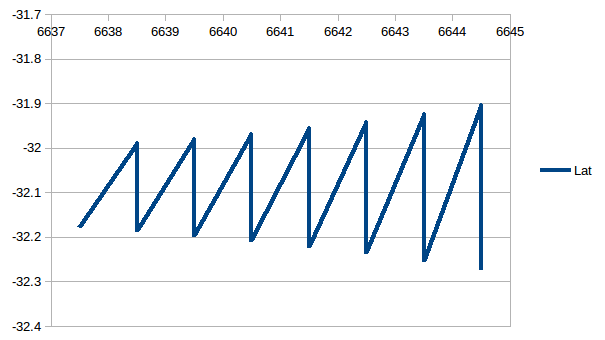
- Calculating your Latitude based on sun rise and sun set times.
- Some code to try.
- A box to put the electronic in.
- What could be so hard with samping daylight:
- The need for an accurate Real Time Clock
- The rotary encoder as an input device
- Code to read the rotary encoder
- A menu system
- Setting the time
- Saving your data
- Remembering settings
- Downloading your data
- Dealing with power outages (restarting as if nothing happened)
- Processing your data:
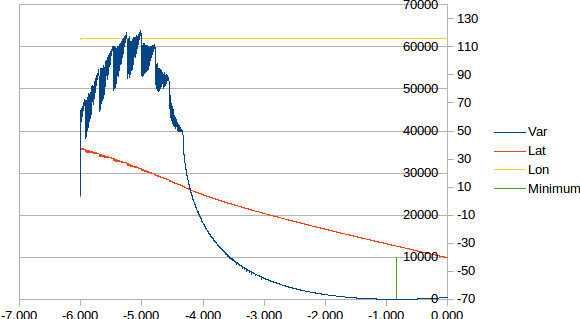
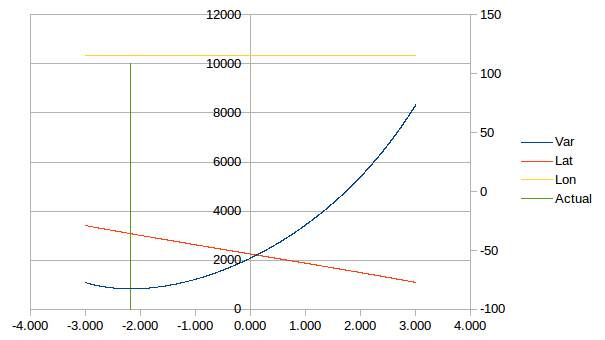
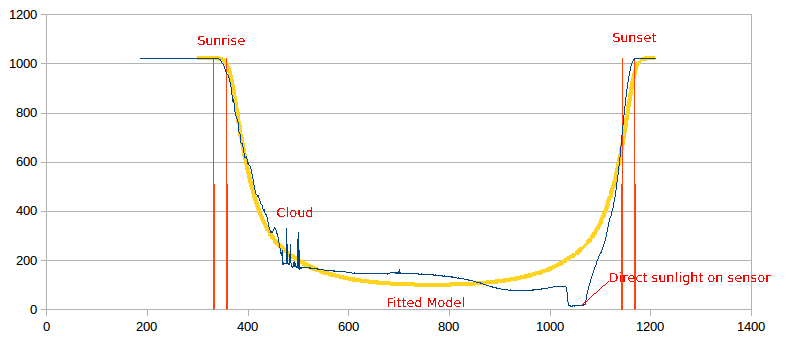
- Using a "solver" to fit a model to the collected data
- The solver
- Creating a model
- Getting an initial estimate
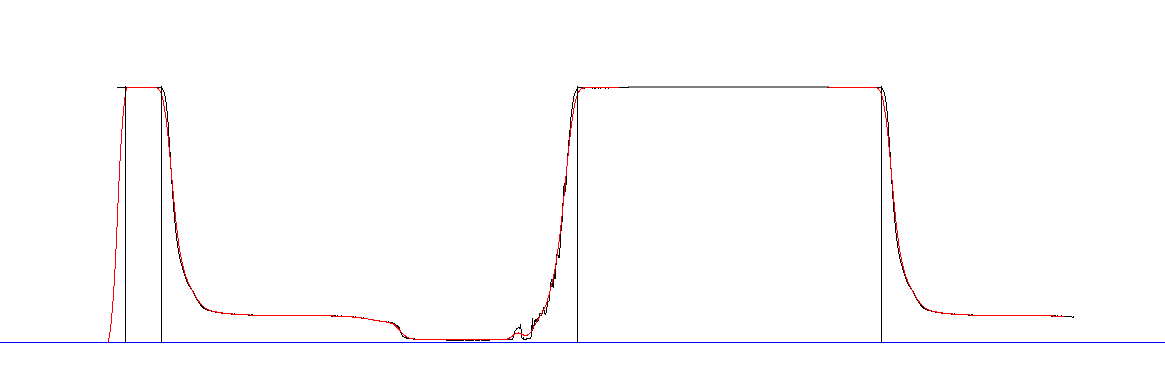
- Dealing with cloud and sensor locational issues
 agp.cooper
agp.cooper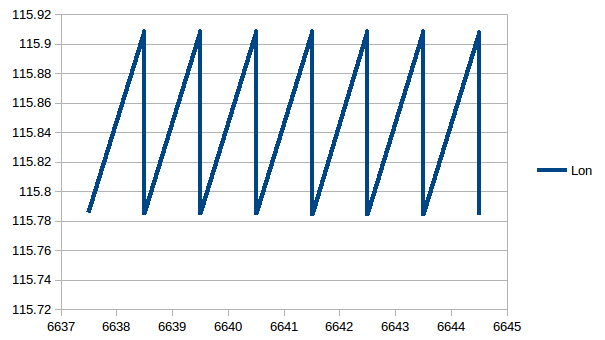
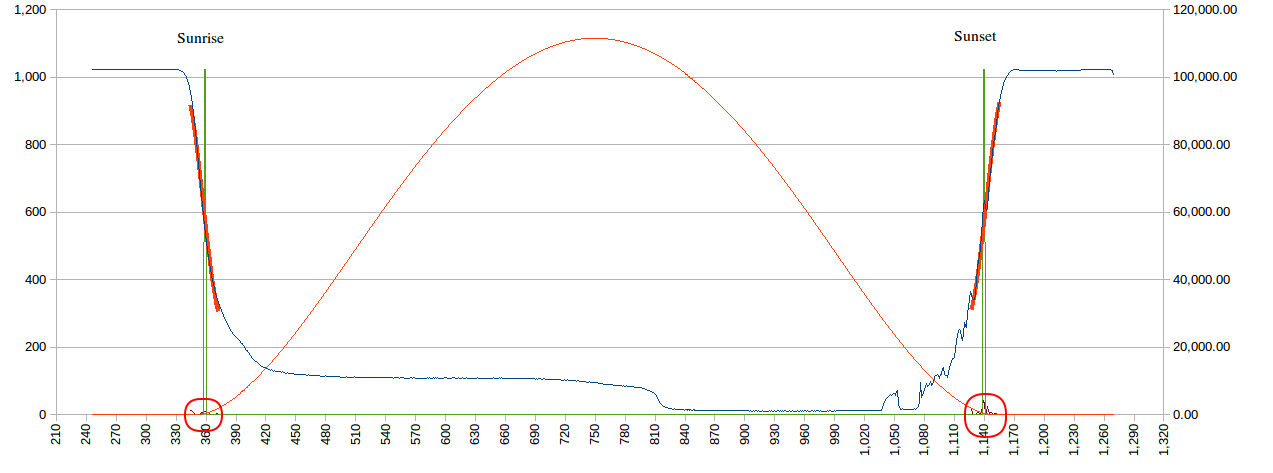
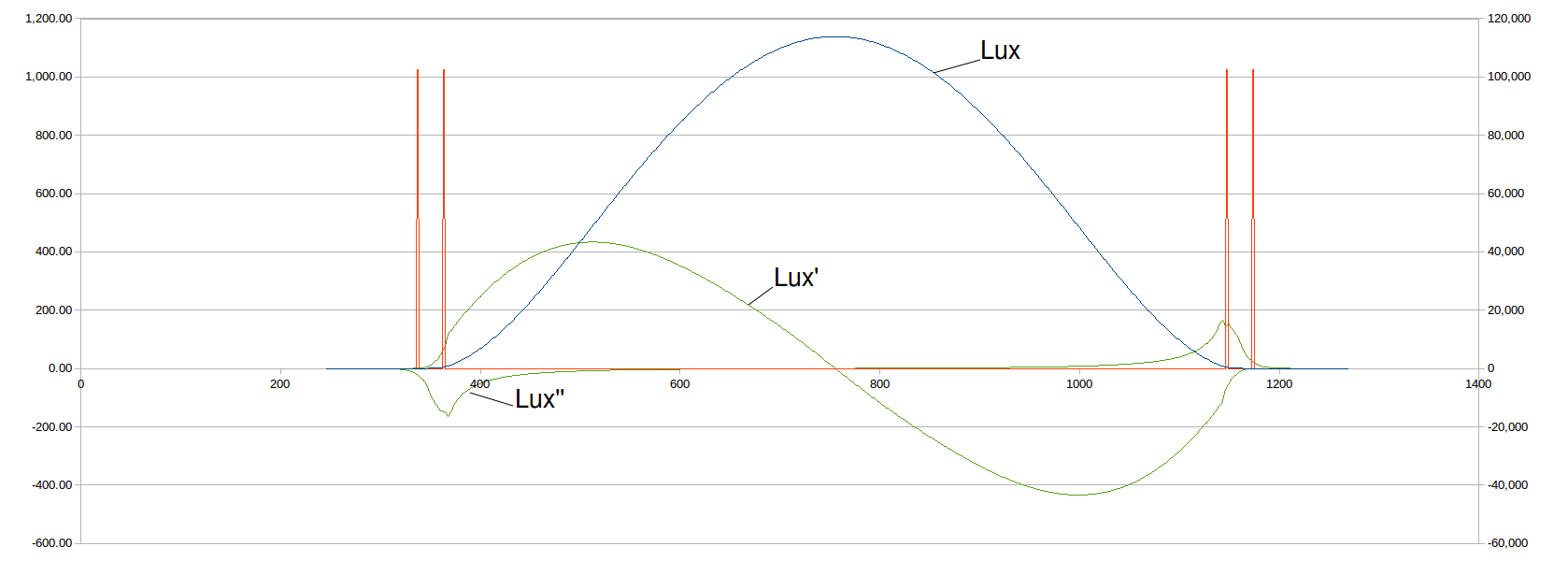
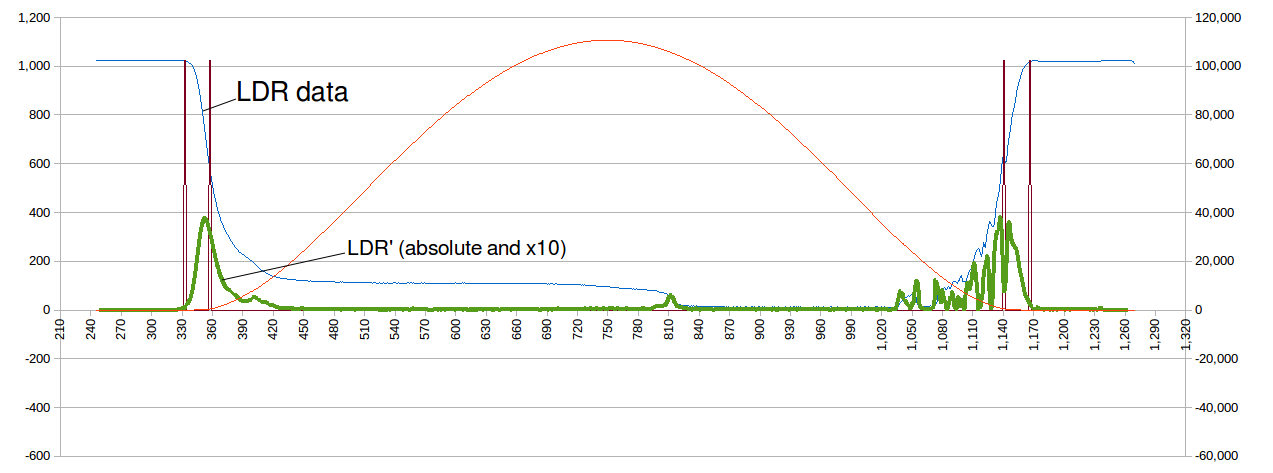
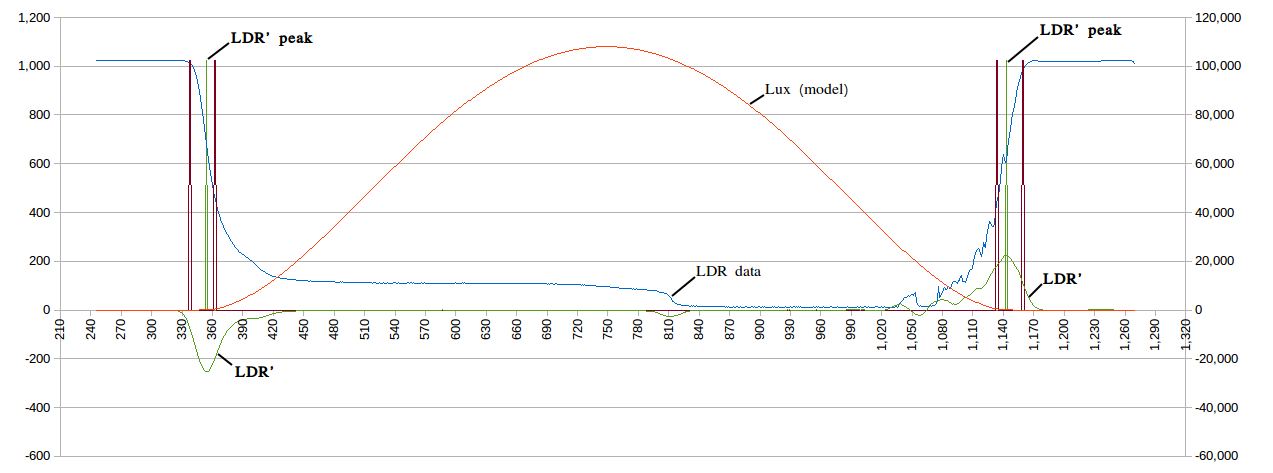
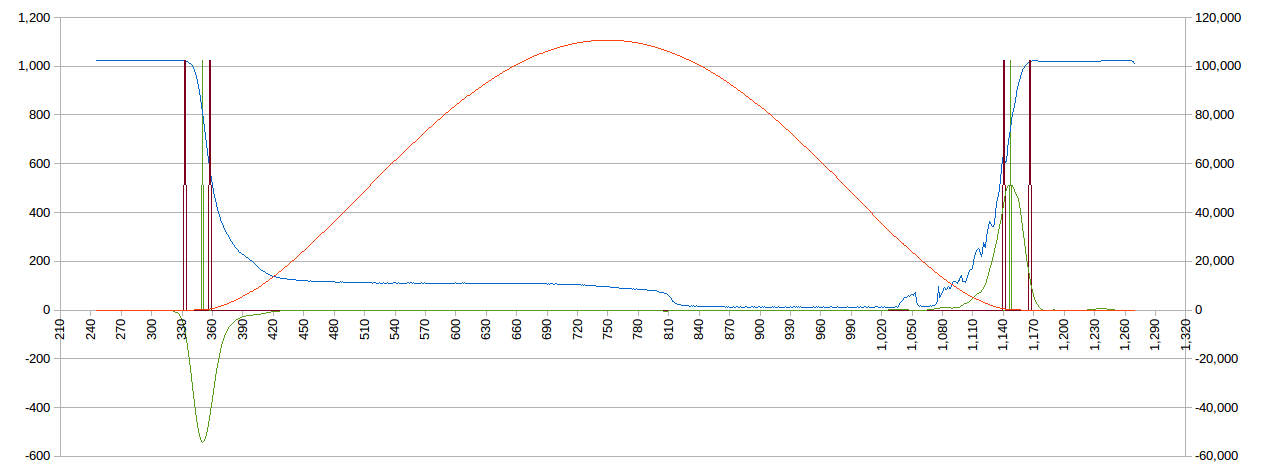
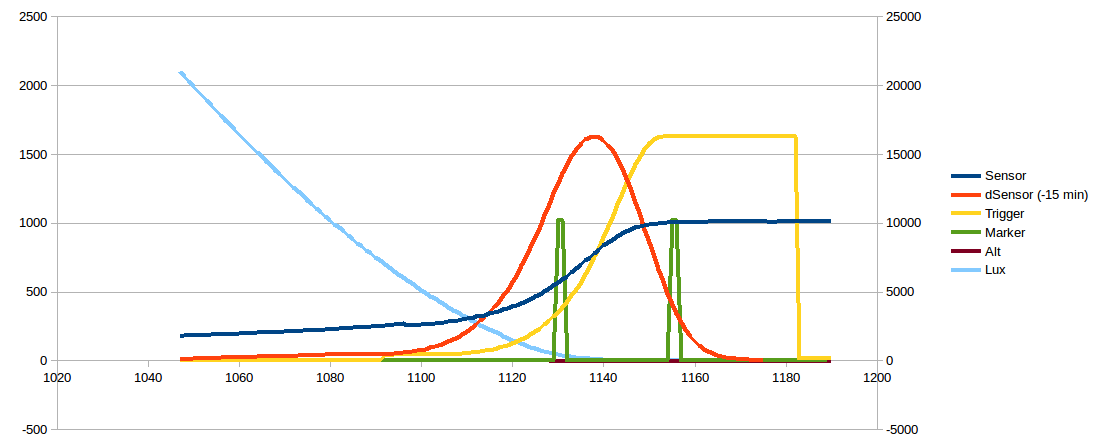
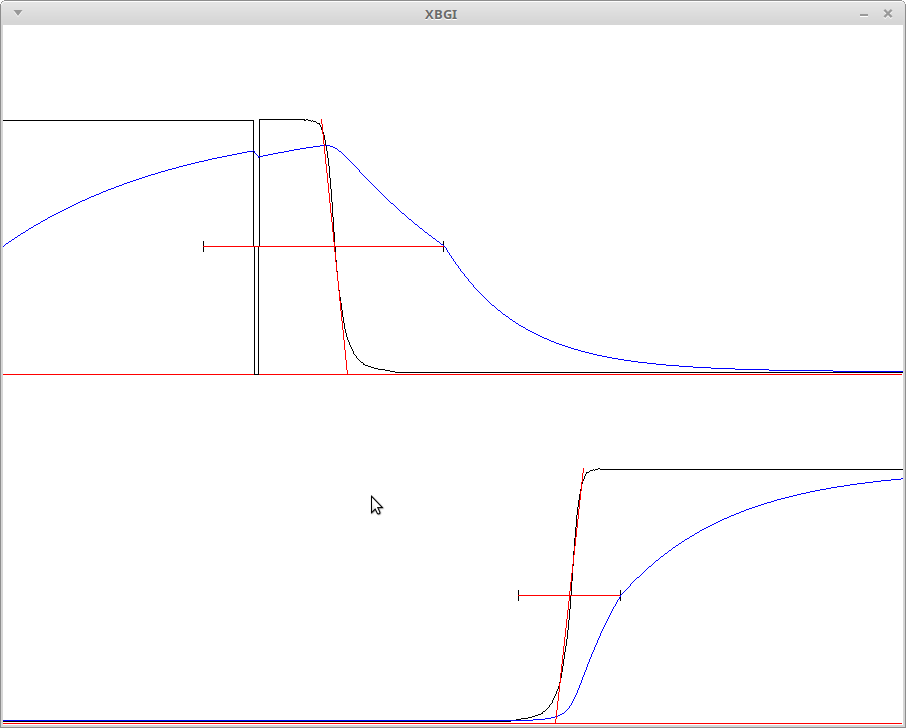
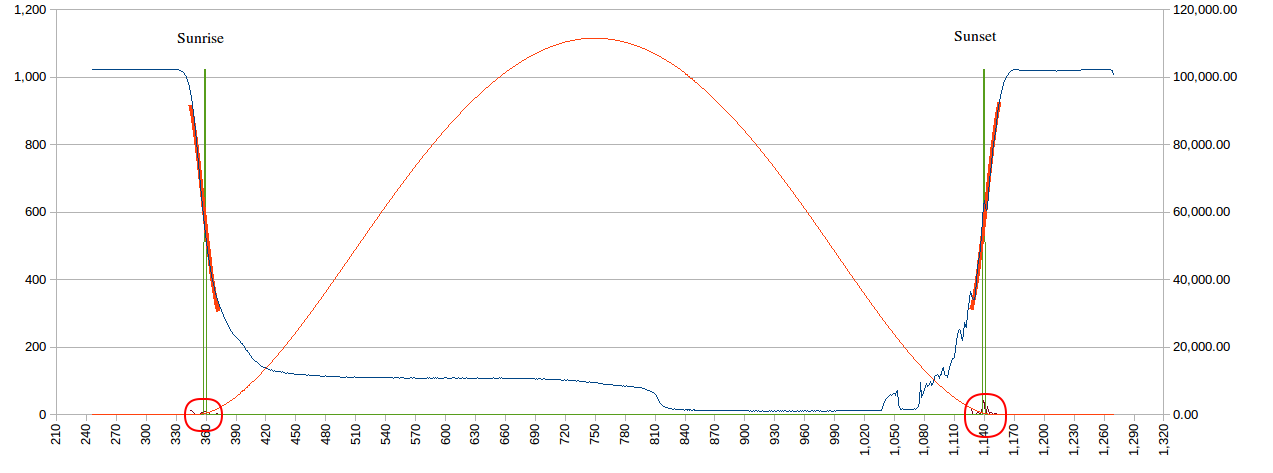
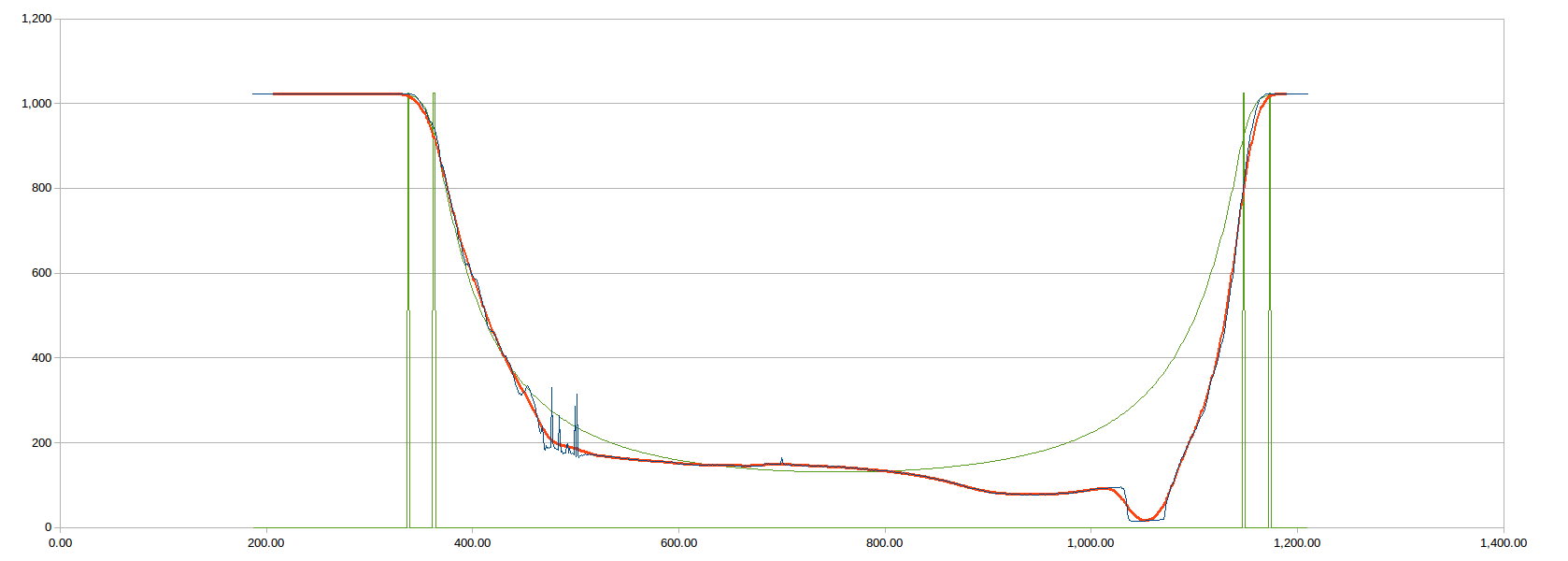
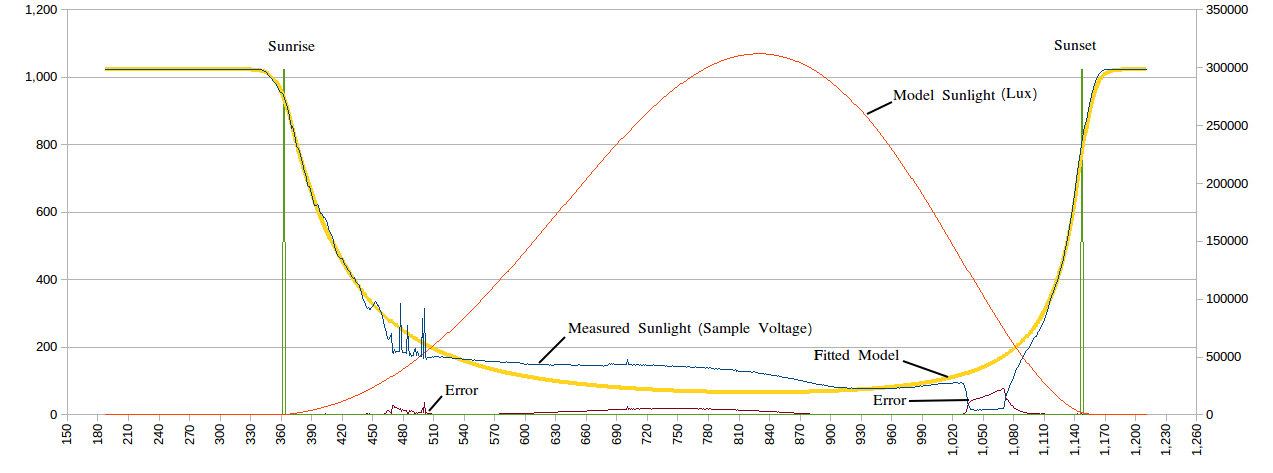
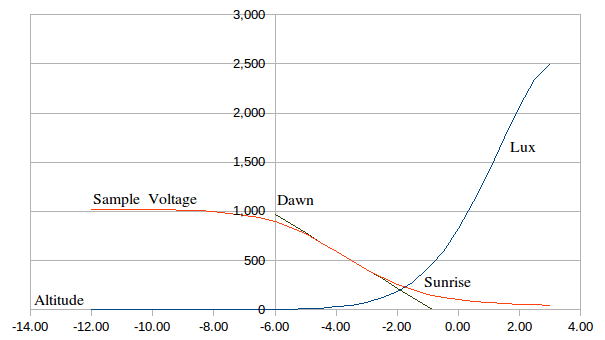
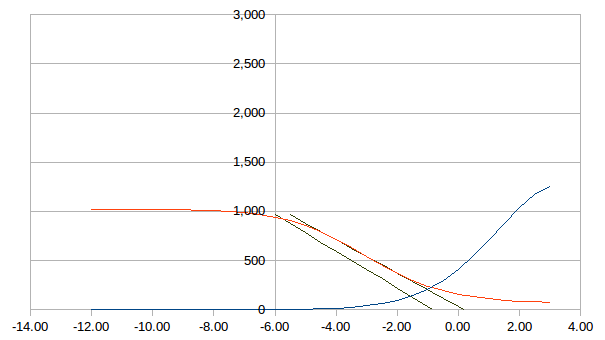











 thjubeck
thjubeck
 jobinpthomas1
jobinpthomas1
Checked FM RDS and only clock signals are in Tasmania (~3000km).
Its only 8000km to Toyko which has 40kHz and 60kHz signals.
May be able to pick these up from time to time for updates (another project!).
AlanX