The magnitude of the FFT is approximated as |amplitude|=max(|Re|,|Im|)+0.4*min(|Re|,|Im|).
This approximation is accurate within about 4%.
The log is approximated as described in (Generation of Products and Quotients Using Approximate Binary Logarithms for Digital Filtering Applications, IEEE Transactions on Computers 1970 vol.19 Issue No.02). This requires that the most significant, nonzero bit be found, then requires four additions and three shift operations based on the position of the bit. Evaluation of the algorithm as a matlab program is here. A C code implementing a realtime spectrum analyser is here.
PIC32 GCC code for the log operation (assuming 16:16 fixed point input/output) follows, where fixed_043 is the fixed point representation of 0.043 and fixed_16 is the fixed point form of 16.0.
sx = input;
y=1; ly=0;
while(sx>1) {
y=y*2; ly=ly+1; sx=sx>>1;
}
log2_input = ((ly)<<16) + fixed_043 + (int)(((unsigned long long)(input-y)<<16)>>ly)-fixed_16 ;
 Bruce Land
Bruce Land
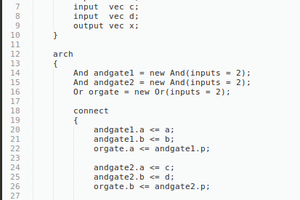
 Reed Foster
Reed Foster
Good to know that there is an approximation.
I cheated and combine the square root and dB (20*log) into a table look up as I only needed a very low resolution (5-bit) for plotting.