A technique for sharpening the spectrogram uses information from the phase spectrum to sharpen the amplitude spectrum. The scheme locates simple sinusoids, linear chirps, and impulses at the correct frequency or time with a higher resolution than the inherent FFT resolution tradeoffs. The basis of the calculation is that the instantaneous frequency (IF) in each FFT frequency band is equal to the first time derivitive of the short-term FFT (STFT) phase at frequency ω and time T:
IF = ∂/∂t(arg(STFT(ω,T)))
and the local group delay (GD) at frequency ω and time T is approximately
GD = ∂/∂ω(arg(STFT(ω,T)))
where the function arg returns the phase angle of the transform (see Fulop).

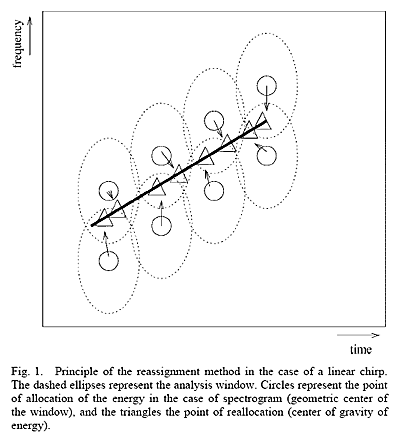
Chassande-Mottin, et.al. show that reassignment is equivalent to moving energy up the local gradient of intensity of the spectrogram (for Gaussian windows). This higher precision does not violate basic time/frequency uncertainty (see Gardner and Magnasco). There is still mixing between reassigned frequencies or impulses which are close together. Plante, et.al. illustrate this with a nice figure shown to the left. Each elipse represents one frequency-time cell of the STFTs which make up a spectrogram. The energy in the cell is is placed at a location determined by the IF and GD.

An online matlab reassignmentt code (Fitz, 2008) was modified for faster rendering and more straightforward selection of minimum plotting amplitude and rendering method. The modified raspecgram and ratoplot (called by raspecgram) produce a reassigned spectrogram, but require a few other routines from the Fitz site. The code runs in Gnu Octave as well as matlab. There is also reassignment code at mathworks.

Examples show the effect of the reassignment.

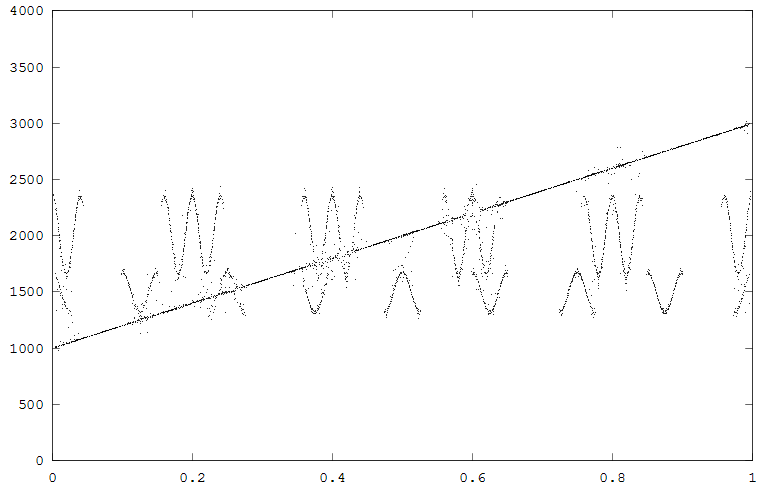
The first example generates two FM signals, with a superimposed linear chirp. The waveform and spectrogram are shown the the first figure, the reassigned spectrum in the second figure. Note that in much of the reassigned plot the FM signals and chirp are well localized, but when they approach each other some scattering occurs. Scattering can be optimized (as usual in a spectrogram) by changing the size and overlap of the FFTs used to produce the results. The reassigned spectrogram was rendered using one color for all points above an energy amplitude cutoff. The rendering mode is refered to in the code as fast. The rendering mode format is method_size_marker. For instance fast_1_dot, color_3_circle, color_1_circle are all valid. Valid methods are fast/color. Valid markers are dot/circle.

Waveform and spectrogram of the test signal.

Reassigned spectrrogram of the test signal.

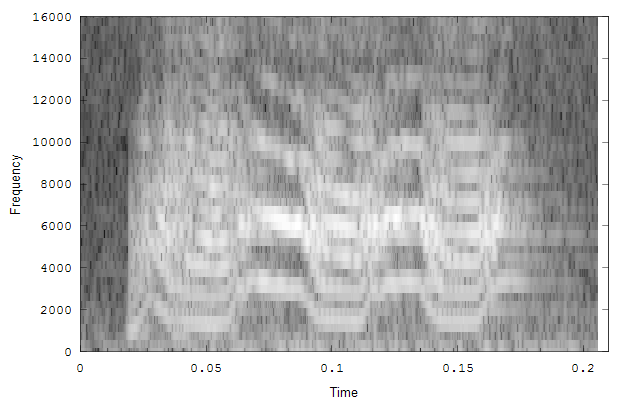
The second example is a nestling green-rumped parrotlet (Forpus passerinus) begging call (thanks to Karl Berg) with a complex multiharmonic, FM structure. The spectrogram of a short segment is shown in the first figure, the reassigned spectrum of one vocal burst in the second figure and another in the third figure. The reassigned spectrogram shows a lot of detailed FM which is hard to discriminate in the original spectrogram. There is enough similarity between the two vocal bursts (and enough coherent structure in each image) to suggest that much of the fine detail revealed is real. The reassigned spectrogram was rendered using four colors for points in four log(energy) bins above an energy amplitude cutoff. Red is highest energy, then yellow, green and blue. The rendering mode is refered to in the code as color_1_dot.

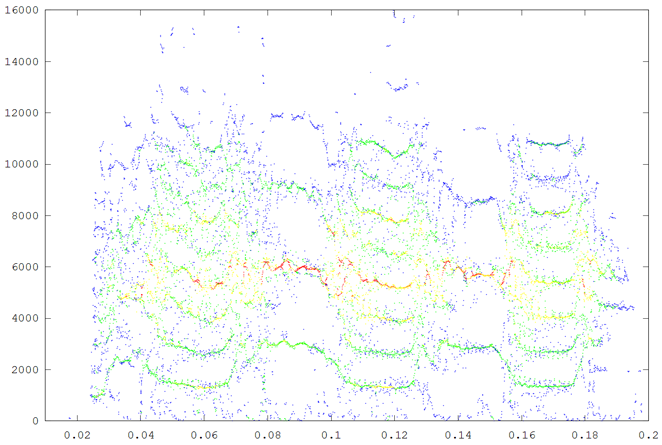
Spectrogram of a short segment of the parrot song.


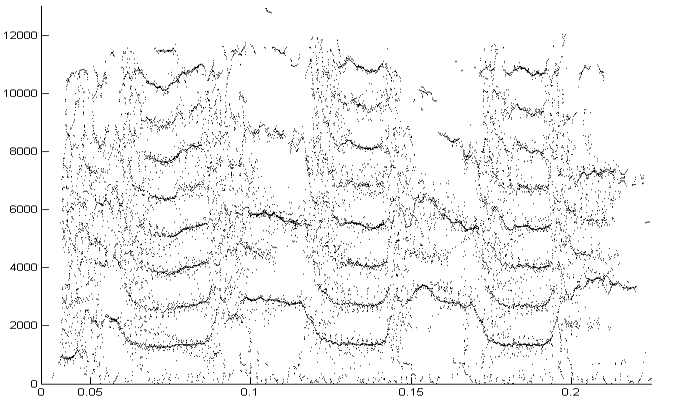
Reassigned spectrogram of the above segment

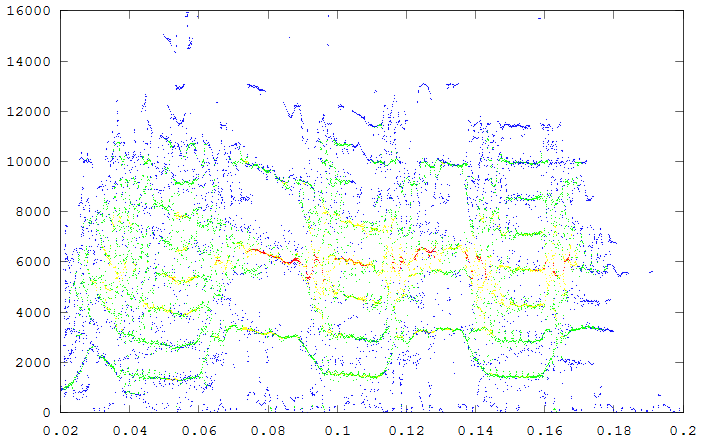
A second segment of the same song to show repeatbility. (click to enlarge)

The third example is a boat-whistle call of the gulf toadfish (Opsanus beta) (Thanks to Luke Remage-Healey and Aaron Rice). The sound is a short noise burst followed after a pause by steady, harmonic-rich hoot. The image pair shows a short segment analysed with a 512 point STFT and 90% overlap...