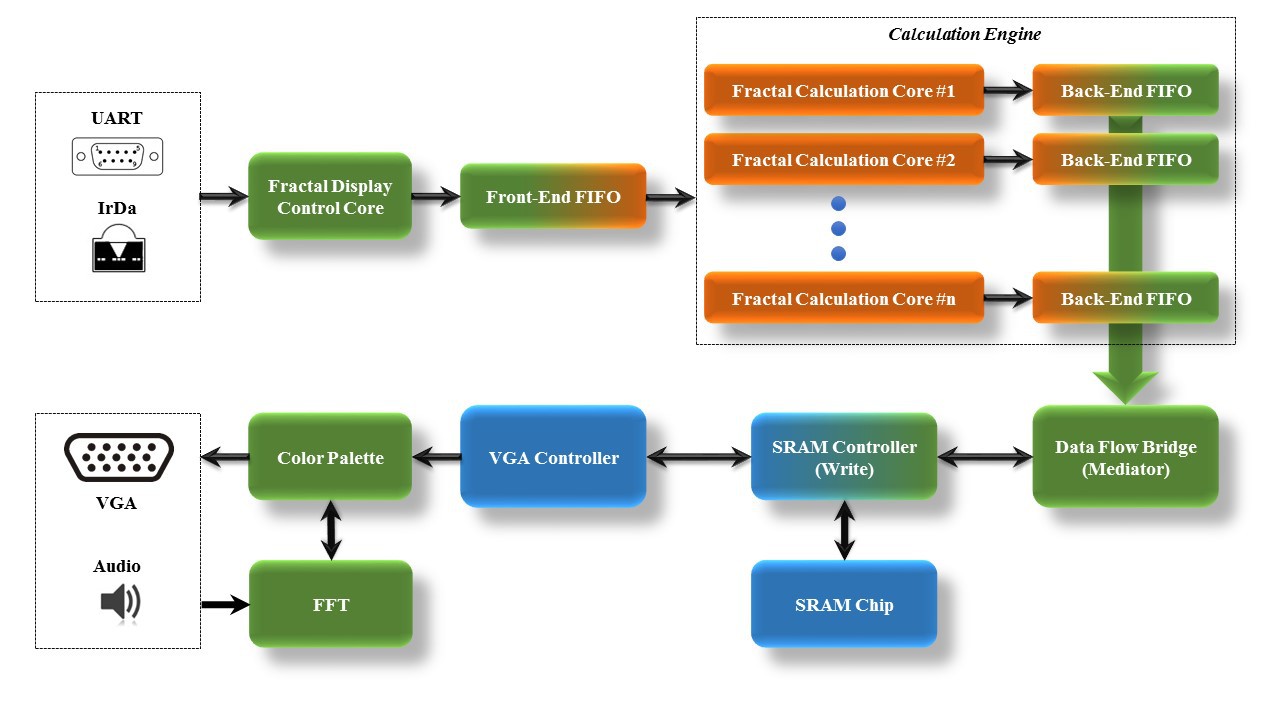
As mentioned in the introduction, there exists two core designs in this project. One of the important designs would be Mandelbrot Calculation Engine, since its performance would directly impact the screen refresh fluency during PAN and ZOOM process. The other key design would be the FFT implementation and color mapping solution. The audio presentation via color rendering actually depends on the color mapping solution. The whole system block diagram is shown below:
The whole system demo video is shown below.
Mandelbrot Set Calculation Engine Design
The Calculation Engine is composed of multiple calculation cores. Each core is responsible to calculate the number of iteration for one single pixel. To maximize the performance of the calculation core, pipeline strategy is applied widely in core calculation units ( subtractor, multipliers, adders ). All core calculation units are generated via Quartus MegaWizard Generator with appropriate pipeline stages. The data-path of calculation core is shown below.
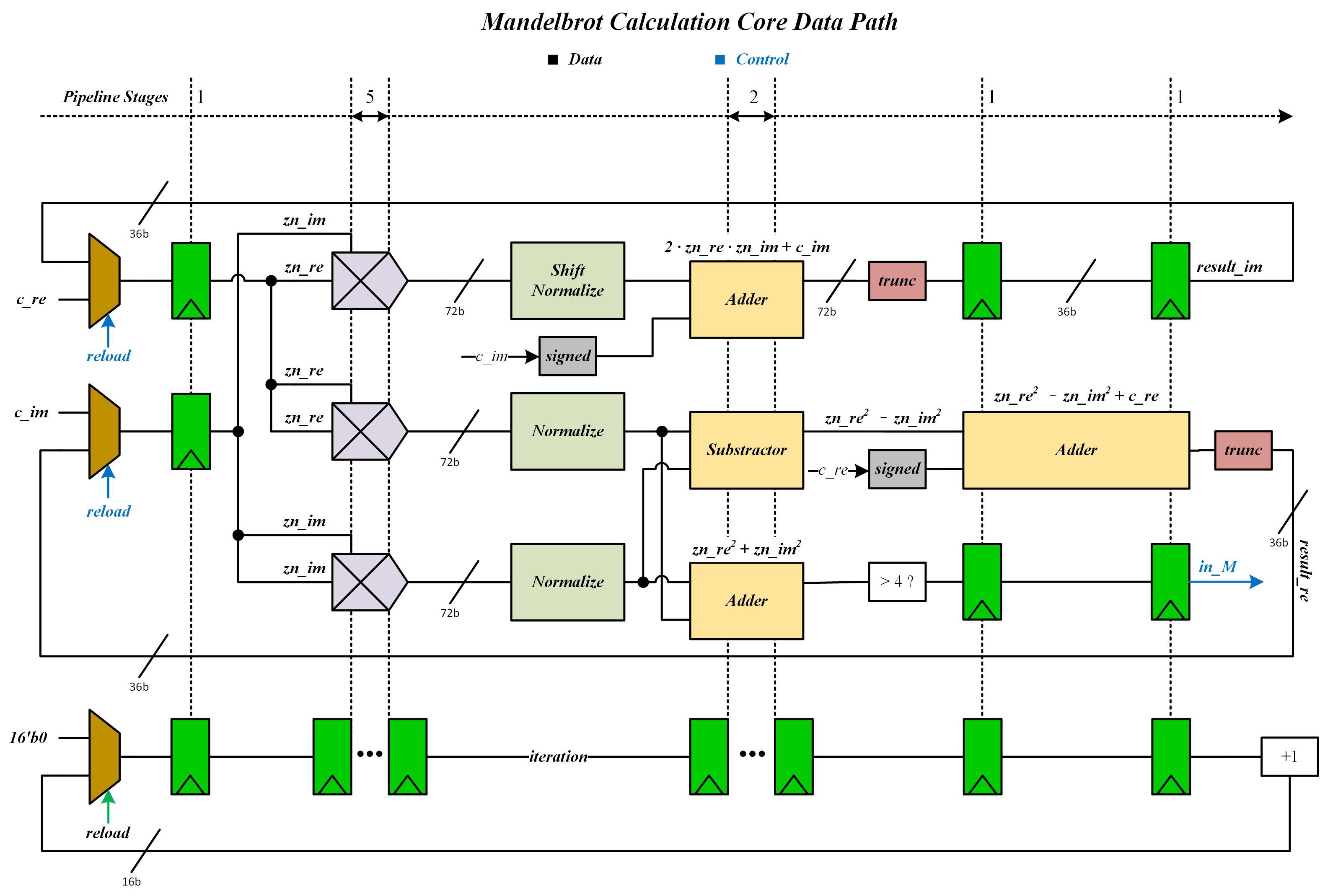
We need to carefully handle some details to guarantee the calculation efficiency and maximize the hardware utilization. Fixed point math is applied in this project since its calculation is much faster than floating point math. Specifically, I chose to use 36-bit fixed point math (Q3.33 - 3 integer bits and 33 fractional bits), since the hardware multiplier for EP4CE115 is 9-bit. Clearly, if a single 36-bit, "un-pipelined" multiplier is implemented, the calculation performance will be limited by it (the critical path will definitely be in this 36-bit multiplier). Based on this consideration, the 36-bit multiplier was pipelined with 5 stages while the adder and subtractor were also pipelined with 2 stages to increase the core performance. In order to improve the accuracy of fixed-point math calculation. All truncation units are designed after the core calculation units. All adders / subtractor are 72-bit. Note that, all control signals generated or calculated during the calculation process must also be pipelined to 10 stages.
Based on the data path design shown above, the total number of pipeline stages is 10, and the calculation clock frequency was tuned up to 150MHz. Please refer to my final report - Hardware Design for more details.
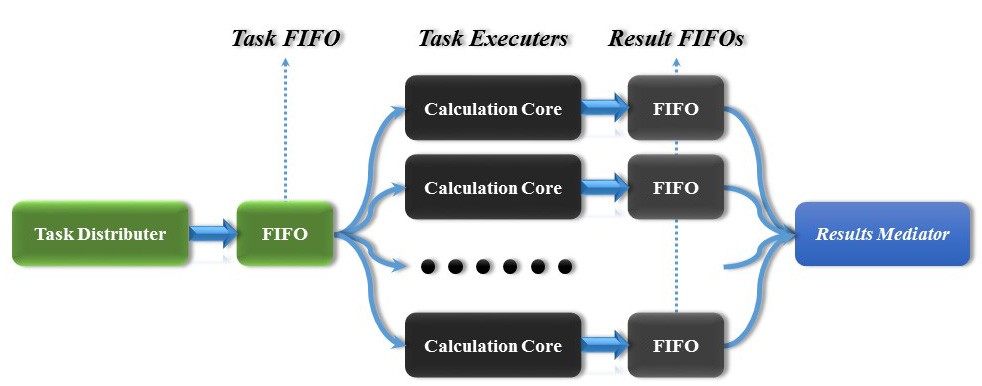
As for the calculation engine design, except for multiple calculation cores described above, a Task-FIFO and multiple Result FIFOs are also implemented as a bridge between high-frequency calculation cores and relative low-frequency modules ( the maximum frequency for SRAM R/W process is 125MHz ). The calculation engine block diagram is shown below.
FFT Implementation with Color Mapping
OpenCore cFFT module is used in this project to realize FFT audio analysis. Compared to Altera MegaCore FFT module, cFFT is much simpler with explicit interface and simple input / output timing. The block diagram of cFFT is shown below.
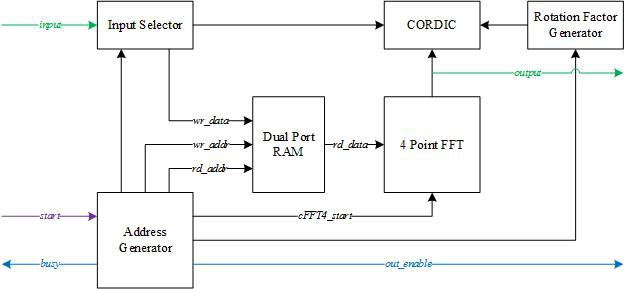
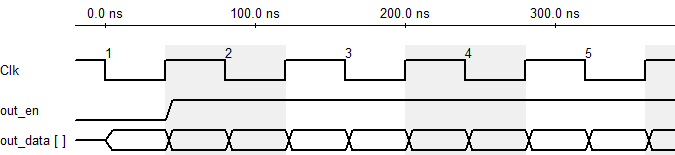
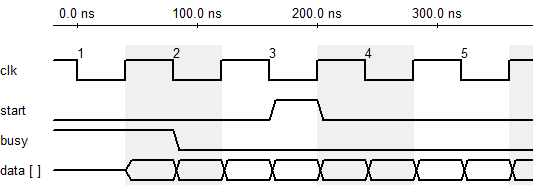
Note that, the output sequence of cFFT is 2-bit reverse ordered. For instance, the 789th (1100010101) output in a 1024-point FFT is actually at 339 (0101010011). The cFFT must be carefully tested so that it can truly represent the audio. A test program is created to verify it. See my report - cFFT Accuracy for details.
With cFFT module, audio input stream in time domain can be easily transformed to frequency domain. The only problem is to map the cFFT analysis results to color space. I implemented multiple color schemes inside the mandelbrot color palette. Each color scheme contain different colors for different number of iterations ( recall that the Mandelbrot is represented by these colors based on the number of calculated iterations ). Note that if the complex point is not in set, the default color is black.
There must exist different solutions to map FFT analysis results to color space. My idea is to change partial colors within a color scheme while...
Read more » Wancheng Zhou
Wancheng Zhou


 Sundance Multiprocessor
Sundance Multiprocessor
 Santiago Germino
Santiago Germino
 rossumur
rossumur
 SHAOS
SHAOS
Awesome project - I love the color mapping. Reminds me of pallete rotation back in the days of VGA graphics and Demos!