Please note: The project log really is a log. I add an update for virtually every change of any value whatsoever. Sometimes I add updates of no value whatsoever. Because.
If you just look at the most recent log updates it will not make a lot of sense because I have had to borrow or evolve the nomenclature for a physical implementation of ternary circuits and because I am not describing a finished product. I am describing an ongoing process complete with wrong turns, errors, conclusions, and solutions. The best way to view this project is from the beginning.

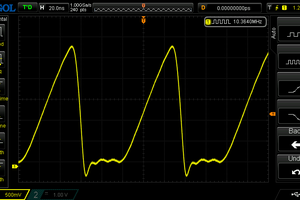

 Yann Guidon / YGDES
Yann Guidon / YGDES
 DosFox
DosFox
Very cool project! Maybe you have already read it, but I have found this 192 page report to be very interesting: http://xyzzy.freeshell.org/trinary/