https://github.com/ChristianLerche/3DPCB - Files are here
GitHub 4 layer, A5984 Edge - Four layer board here - Modified to accept 24V.
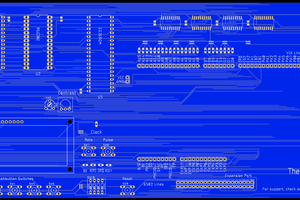
The 3DPCB is a Smoothie-compatible PCB designed to fit "normal-sized" 3D printer driver boards.
To make the experience fit your profile, pick a username and tell us what interests you.
We found and based on your interests.
https://github.com/ChristianLerche/3DPCB - Files are here
GitHub 4 layer, A5984 Edge - Four layer board here - Modified to accept 24V.
It's time to log something.
The 3DPCB has been revised a bunch of times since I first came up with the design (Proudly stole the schematic from www.smoothieware.org).
From 2 to 4 layers, extra drivers, doubling the power-MOSFETs, and a bunch of rewiring.
Now the github has all the info of the project. I have a bunch of PCBs which is unassembled, as I actually don't have enough printers for them. GO FOR THE A5984 EDGE!
The design is not cheap like the chinese copies of Smoothieboard, but hey, I wanted to design my own.
EVERYTHING IS TESTED, ROCK SOLID PERFORMANCE!
https://github.com/ChristianLerche/3DPCB-4LAYER
It's 4 layer so heat transfers will be better.
Minor updates to the design.
When I have a tested board, I will write a new log.
Create an account to leave a comment. Already have an account? Log In.
Hey, like on instagram - P2.10 needs to be low during reset, then it will talk to your programmer ;)
i did that but still wont work. also where did you source the chip from ? which programmer did you use?
I used a cheap CP2102(or 03) maybe - The chip I got from RS components :)
Hi, I was wondering if your Github for this is up to date for the 4 and 2 layer pcbs? As I see that they were updated several years ago, but your latest log here is recent.
Have either been tested? And what's the main differences between the 2 layer and 4 layer? I am interested in learning from your design in order to design my own. Just want to make sure I'm learning from something that is tested/works.
Go for the 4 layer A5984 edge version. Better heattransfer, better stepperdrivers. :)
it would have been great if the drivers were socketed. I am not very familiar with kicad ( use eagle ). i will try to do it after i get a hang of kicad.. ( need a smoothieboard for my next project )
Christian did you put anymore work in this right now? I would love to try this out.
Sure did, I'm in the middle of assembly of one more board - 4 layers, 5 stepper drivers, 4 mosfets, and a little rearranging of the components.
When I've had the time to assemble it, and have tested it, the finished files will be on github.
Please do write every now and then in here, as I often go to other projects, like my house and so on.
Thanks!
Thank you for your fast reply!! I would like to try out the 2 Layer PCB. But on your Github you wrote that these aren't working right now. Do you have a fixed version i could try?
"Thank you for your fast reply!! I would like to try out the 2 Layer PCB. But on your Github you wrote that these aren't working right now. Do you have a fixed version i could try?" - Sure thing. I'll do a checkup today, to see if everything is fit for fight - If you are interested I'll send you a 4 layer PCB free of charge, if you can wait until I have tested the PCB. Or just want to dive into the unknown? ;D
It would be great if the 2 Layer PCB Layout would be in good shape :D
I would love to try your 4 Layer PCB, when you have tested it. Of course i would take over the cost for shipping.
- If you go here: https://github.com/ChristianLerche/3DPCB - It actually should be the fixed version for two layers.
Do a check however in KiCAD to be sure it's okay.
Any movement on the Rev. B commits to your repo? Really would like to take a look at this.
Sure, I'll add it tomorrow. 18 hours tops :) Thanks for letting me know :)
https://github.com/ChristianLerche/3DPCB - IT'S NOT WORKING AS OF RIGHT NOW! I started adding changes some time ago without git, so I have to go over the PCB soon. But you'll get the idea! :-)
Become a member to follow this project and never miss any updates
 Josh Kittle
Josh Kittle
 bobricius
bobricius
 Mike Tripoli
Mike Tripoli
 Lukasz
Lukasz
how did you program your lpc? I have been going nuts trying to get it into isp mode. I am not using your board but a similar cor3d board .