Intoduction:
Kalman filters can be intrepreted as Bayes filter with the gaussian linear case. There application range from economics to weather forecasting to satellite navigation. If models are not linear the beliefs do not remain gaussian and we can not work with a simple kalman filter.
A multivariate Gaussians can be described:Let v be a multivariate gaussian distribution:
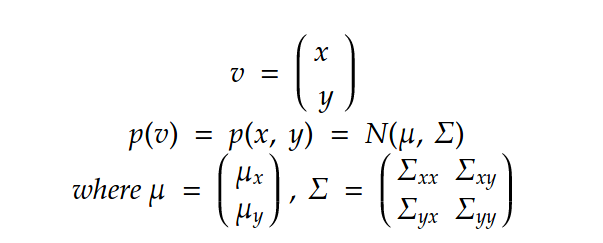
The marginal of x can be defined as:
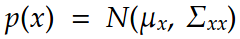 The conditional of x with respect to y is:
The conditional of x with respect to y is: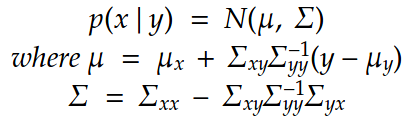 The kalman filter linear and observation models can be thus represented by:
The kalman filter linear and observation models can be thus represented by: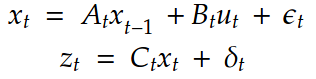 where x represent the motion model and z represent the observation model. Here the motion noise epsilon is zero mean gaussian with covariance R and the observation noise is zero mean with Q covariance.
where x represent the motion model and z represent the observation model. Here the motion noise epsilon is zero mean gaussian with covariance R and the observation noise is zero mean with Q covariance. Substituting these values in the Bayes filter motion and observation models we get,
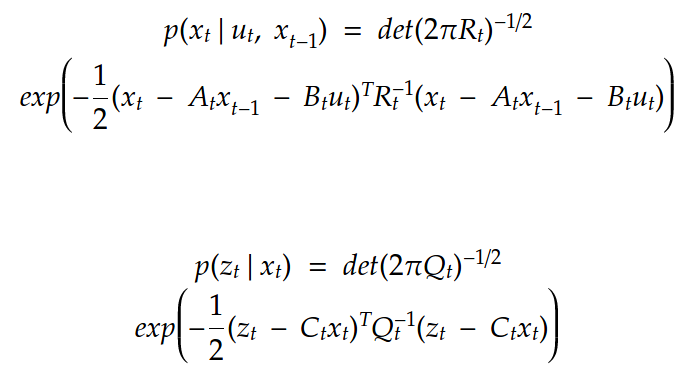 The above values can be substituted in the prediction and correction step below:
The above values can be substituted in the prediction and correction step below: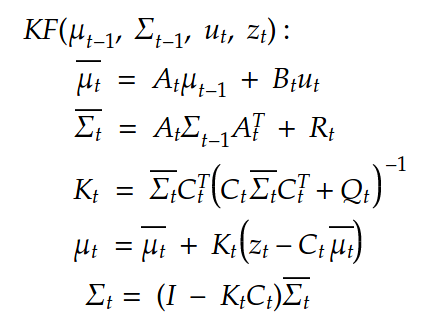 The first two equations show the predictions for the mean and covariance of the state and the last two equations give us the final belief of the state considering the observations. Once again, all of this is just applicable when we have linear motion and observation model. For non-linear models we consider the Extended Kalman filter that I would be explaining in my next post.
The first two equations show the predictions for the mean and covariance of the state and the last two equations give us the final belief of the state considering the observations. Once again, all of this is just applicable when we have linear motion and observation model. For non-linear models we consider the Extended Kalman filter that I would be explaining in my next post. int-smart
int-smart
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.