Now, before we dive in, a few notes:
If you've had a go at solving these puzzles (properly, or otherwise) I'd love to hear about them in the comments.
1) This whole endeavour was completely pointless, as Google indexed all the pages anyway. After sniffing around GCHQ-related things on Friday night, this popped up in my Google Now news feed the next morning - before I had solved anything: (nice one GCHQ - ever heard of robots.txt?)
2) Possibly, applying some brainpower would have been quicker in solving some of these things. I wanted to see if brute force was feasible.
3) The only reason it was possible to get as far as I did is because GCHQ were sloppy - they allowed thousands of page requests from the same client, and they left their hashing algorithms in the page source code.
4) "Part 5" is un-brute-forceable. It's a bunch of horribly hard brain teasers. You're on your own for that one (I haven't even tried it yet).
There will be spoilers on this page. I have linked to the actual answers instead of displaying them, but I'm leaving the methods in the clear.
Part 1
This is part 1:
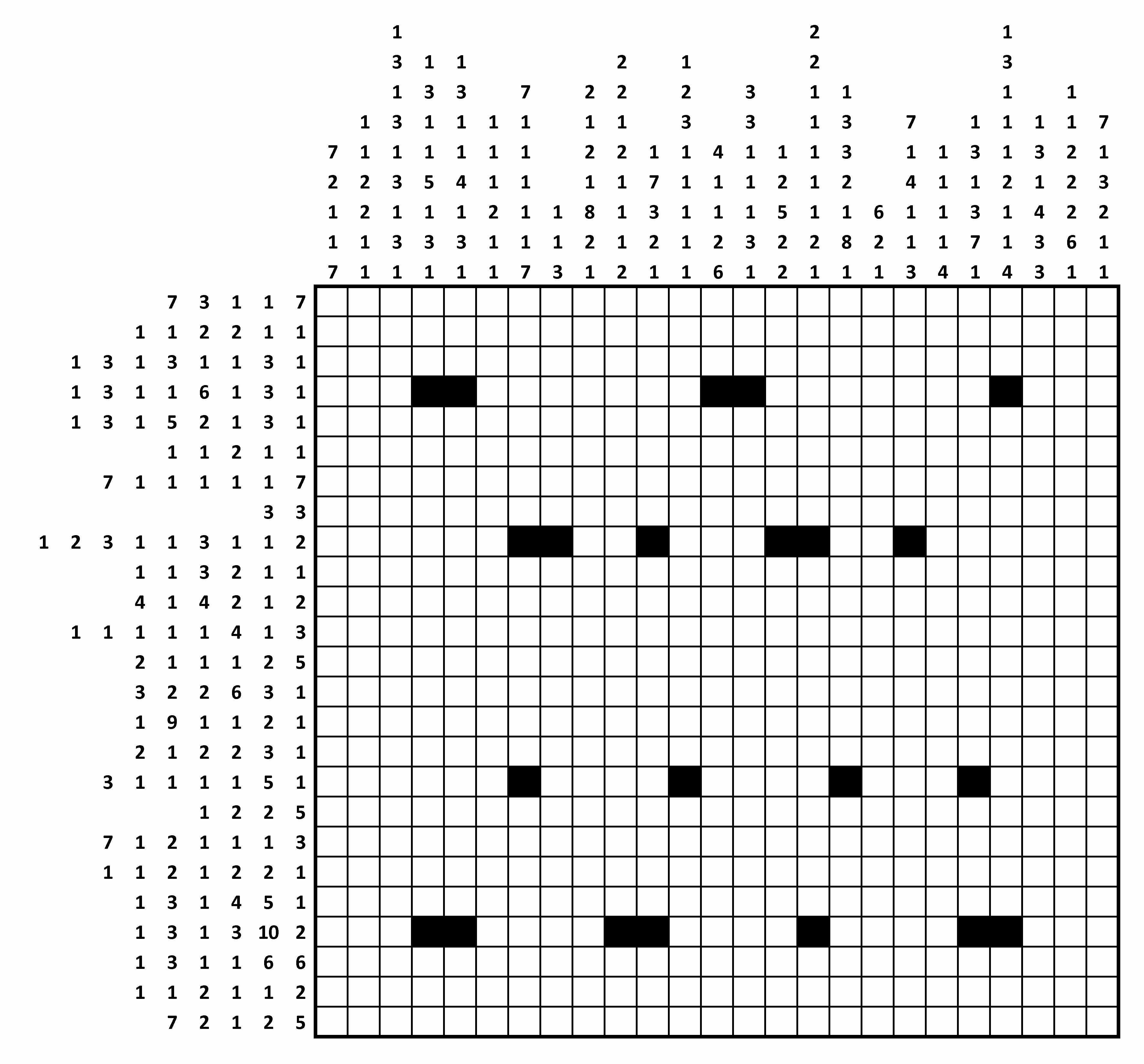
And it comes with instructions:
In this type of grid-shading puzzle, each square is either black or white. Some of the black squares have already been filled in for you.So, the method is going to be somewhat like a Sudoku, except each square has only 2 values, and the possible values are different for each row/column. This should be easily crunchable - the basic plan is:
Each row or column is labelled with a string of numbers. The numbers indicate the length of all consecutive runs of black squares, and are displayed in the order that the runs appear in that line. For example, a label "2 1 6" indicates sets of two, one and six black squares, each of which will have at least one white square separating them.
- For every row (and column), calculate all possible arrangements.
- If the row (column) has a fixed pattern given, then prune any arrangements which don't with with it
- If any rows (columns) have only one possible arrangement now, then treat them as fixed patterns
- Goto 2
We can treat a row as a binary number, 25 bits long with a 1 representing a black square and a 0 representing a white one. This makes the code dead simple (and fast).
Calculating each possible arrangement is a great candidate for a recursive algorithm. We'll basically start at the left and place the first black block (I call them 'marks') in each possible position which still leaves enough space for all the ones after it. In each position, we recurse - placing the next 'mark' in each possible position after the one we just placed... do this for every 'mark' and you get all possibilities. Here's some pseudo-code for the recursion:
/*
* row_info stores things like the number of marks, their width,
* and all the possible candidate patterns
*/
function place_mark(row_info, pattern, start_pos, mark_num) {
/* Recursion termination clause */
if (mark_num == row_info.num_marks) {
/* We are done with this line. Store the pattern */
row_info.possible_patterns.append(pattern);
return;
}
/* Recursion reduce cause */
/*
* space_required(row, mark_num) computes the amount of space required
* for all the marks in row_info after the mark_num'th one.
*/
req_space = space_required(row_info, mark_num);
for all start positions < (25 - req_space) {
/*
* mark_bits(width, start) generates a binary number representing
* a mark of the given width at the given starting position
*/
mark = mark_bits(row_info.marks[mark_num], start);
place_mark(row_info, pattern | mark, start, mark_num + 1);
}
}At each step along the way, if the row has a fixed mask (either because we calculated one from only having one possibility, or because there was some marks in the original picture) we can test each pattern against it, and discard those that don't match.Once we've computed all of these, we "fix" any lines with only 1 possible candidate, and then use that to update the masks on all other rows and columns. When that is done, we "prune" all of the candidates. There are two reasons for a pruning:
- A pattern doesn't match its row mask any more
- A pattern doesn't match any of the candidate patterns in one or more of its counterpart [column/row]
When we've pruned against these conditions, hopefully we are left with one or more rows/columns with only one remaining pattern candidate, so we fix those and start again.
"Prune case 2" above has the potential to be really really expensive - I was worried at first that solving this puzzle could take a lot of computer time. Luckily the pattern converges pretty quickly (5 iterations), and it takes less than a second on my machine (I guess it did have to be solvable by our puny human-brains).
Spoilers:
ASCII output: http://usedbytes.com/misc/gchq2015/part1/part1.txt
Image output: http://usedbytes.com/misc/gchq2015/part1/part1.png
C-Source: http://usedbytes.com/misc/gchq2015/part1/main.c
Part 2
So we get to part 2 - a series of multiple choice questions. I did.. like.. have a go - but it doesn't tell you when you get one wrong (smart!), and they're hard. However I did notice that the URLs are suspiciously similar to the answers you pick.
Bingo, we can just try requesting the page for every single possible combination of answers, and one of them will be correct. I already knew that when you got it wrong, it said "Sorry - you did not get all the questions correct. Please try again." So all we need to do is request pages, grep for that, and the one that doesn't match is our winner.
6 questions, 6 answers each - that's 46,656 possible combinations my by reckoning. So as not to kill the poor AWS server, we'll limit the rate to a couple a second, that should take somewhere less than 6 hours in the worst case. I know it doesn't offer any statistical advantage - but I randomised my URL list so I wasn't requesting like "AAAAAA" then "AAAAAB" in order, and left it running overnight (hoping that GCHQ didn't block my IP in the meantime - even if they did, I was running it from a server "in the cloud" so that I still had a chance to play from home :-) )
Use a little Python to generate the URLS:
#!/usr/bin/python2
import itertools
import random
url_base="http://s3-eu-west-1.amazonaws.com/puzzleinabucket/"
url_extn = ".html"
urls = []
for i in itertools.product('ABCDEF', repeat=6):
prod = ''.join(i)
s = ''.join([url_base, prod, url_extn])
urls.append(s)
random.shuffle(urls)
for u in urls:
print u
And a little bash to wget them all:#/bin/bash
for url in `./get_urls.py`; do
echo -n "."
wget -qO out.html $url
grep -qi "Sorry - you did not get all the questions correct." out.html
if [ "$?" -ne "0" ]; then
echo "Gotcha: $url"
exit 0;
fi;
sleep 0.$[ ( $RANDOM % 10 ) + 1 ]s
done;
Spoiler: And in the morning I was rewarded. I wonder if there's any significance in those letters?Part 3
OK, so Part 3 is more brain teasers. There's 4 answers, each a single word, which you have to put in a form at the bottom and submit.
Of course the first thing I check is if the answers are in the source code (nope) - however the Javascript hashing algorithm used to check the answers was (doh! Come on Guys!).
That's not the whole thing sorted though - the hash isn't like a single-cycle operation, and its result can't really be cached for incremental testing. I had a guess that I could probably manage 1 million hashes/second (this turned out to be pretty close - I can manage around 3.5m hashes/second). If I were to use a dictionary of 50,000 words (reasonable) the number of combinations is:At 1 million hashes per second, this would take something like 72 million days to test them all.
Improving the speed by a factor of a million isn't really feasible and reducing the dictionary is risky because you might remove the words you need. Anyway, I ported the Javascript hash to C (remember to use 32-bit integers), and coded up another recursive algorithm to test every possibility from a dictionary of words and set it going (hey, you never know, I might be lucky!), while I tried to reduce the problem space.
Actual puzzle solving
OK, reducing the problem space means actually engaging your brain. I'm not going to post the answers here, but I solved parts A and C. 'A' was relatively easy. 'C' took a lot of head-scratching and researching dead-ends until I had one single spark of inspiration which turned out to be correct.
I wrote some Python code to show how if you don't want to try solving them yourself:
(for all of my Part 2 solutions you will need a dictionary called "words.list" with one word-per-line - try looking here: http://stackoverflow.com/questions/4456446/dictionary-text-file. I'm not posting my full list because I don't know the copyright on it, but a bare minimum "words.list" is a massive spoiler here)
OK, so now I know 2 of the words, I've reduced the search space by a factor of ~2.5 billion, leaving a nice manageable 2.5 billion combinations to try.
Some modifications to my brute-force code allowed me to fix the words I had already found, and then I set it going. A mere 3.5 minutes later:
$ time ./a.out
Loading 62602 entries. maxlen: 28
Done. Loaded 62602 of 62602
643825664 hashes computed
Found match. Tried 644718383 combinations.
A: SPOILER
B: SPOILER
C: SPOILER
D: SPOILER
real 3m31.416s
user 3m31.400s
sys 0m0.000s
Wahoo! This took ALL DAY to figure out the two words needed to make it feasible. I was well chuffed that the brute force approach could save the day again.I guess it's possible that the hashing algorithm could have a collision - but it it does I didn't hit it because my answers worked fine.
Part 4
Part 4 looks a lot like part 3, except you have to find numbers instead of words. They also tell you that the numbers make up an IP address (nice! that means they have to be 0-255, that's easy!). A quick check in the source code reveals the same Javascript hash they used last time! Excellent, this will be dead easy.
One complicating factor is that there are only 3 numbers, but we need 4 to make an IP address. I assumed that this meant one of them had a decimal point, and made the needed modifications to my code to support that.
In the previous challenge, each word had a NUL byte ('\0') between it. We need to make one of those into a '.', so I run the recursion 3 times, replacing one of the '\0' separators with a '.' on each pass. This gives 3 dot positions and 4 numbers with 256 possibilities each:
For part 3, I could compute around 3.5 million hashes per second. This time around, the hashes will be shorter on average (max length of 3 + 1 + 3 + 1 + 3 + 1 +3 = 15), so this number is easily achievable. Let's hop to it. This time instead of reading the dictionary from a file we'll just build one containing all the possible numbers (as strings: "0" to "255").
$ time ./a.out 5168431104 hashes computed Found match. Tried 5169371089 combinations. A: SPOILER B: SPOILER C: SPOILER D: SPOILER real 14m2.907s user 14m2.653s sys 0m0.177sSo we tried around one third of the combinations, at a rate of a little over 6 million hashes per second. Of course you could speed this up by stripping out invalid or reserved IP address, but that would have taken longer :-). By the time I'd finished breakfast, this had already given me the answer.
Fin
So that's it - all 4 stages cracked, and I only had to solve 2 of the nasty cryptic questions. Unfortunately, by bypassing all of the earlier work, my brain probably isn't warmed up enough to manage any or Part 5. C'est la vie!
In all, GCHQ could have made this a LOT harder by doing the hash server-side, and my preventing Part 2 request spamming. I'm glad they didn't, this way was fun.
Happy hacking! :-)