So the cell was decided to be an equilateral triangle whose sides measure 62.5 mm... But why?

One of the goals for the MOSAIC LS project is scalability. How do you shape a component that can conform to any application thrown at it, scalable? Why, triangles of course!

... Triangles are forever...

A triangle is the most basic enclosed shape that can be formed with the least number of sides, 3 in this case. Its used in graphics to reduce the number of vertices in a mesh while retaining the most detail as well as in structural engineering. With triangles you can assemble them into whatever pseudo shape you want. They can approximate circles, rectangles and its not limited to just 2D shapes. They can approximate spheres , rings, domes, boxes, cylinders, etc.

So that addresses what shape to make the "cell" into - an equilateral triangle which keeps things as symmetrical as possible. But what about its size, how big should it be? Too small and complexity becomes an issue as more are required. Too big and it might hinder certain application constraints such as portability or tight spaces.

... Who said size doesn't matter?...

To address the question about how big to make the triangular cell, first we have to consider what applications the MOSAIC LS cell could be used in. One of the key applications that had a heavy weight on design considerations was solar. Many projects out there use solar as their method of energy collection, storage and usage.

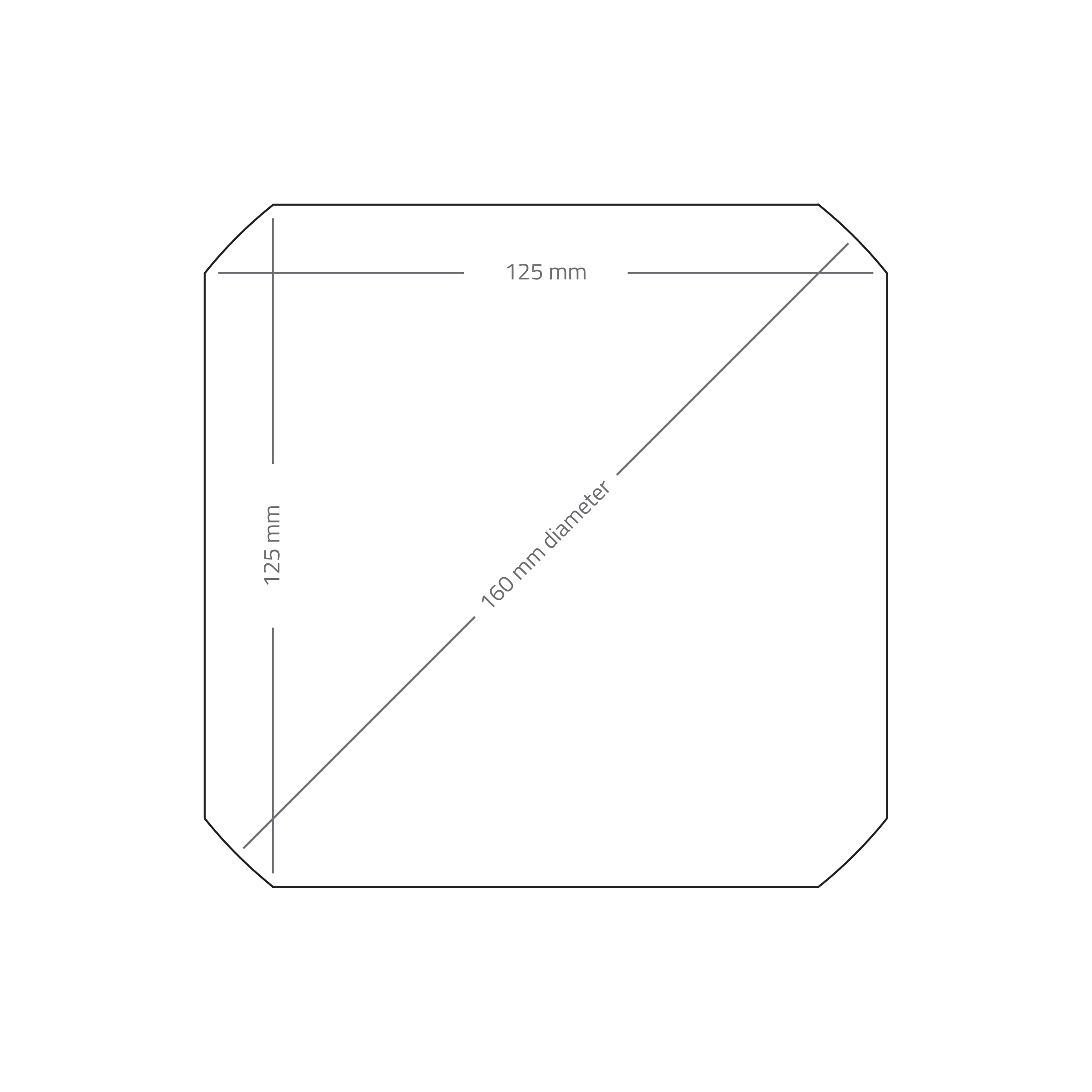
After a few deep dives on the 'webz, some querying around work and physically measuring dimensions of cells in solar panel assemblies, a conclusion was reached. The most common size of solar cells (monocrystalline or polycrystalline) was a pseudo-square cut from a 160mm diameter ingot of silicon. It measures 125mm x 125mm with corners of 160mm diameter. See Figure 1 above.

If a cell were to be designed with the sides of the triangle measuring 125mm, then one would be left with 1/2 the solar cell uncovered. However if a circle with a diameter of 125mm is considered, it will cover approximately 75% of the cell. The best approximation of a circle using the least amount of triangles is a hexagon. That means there are 6 equilateral triangles whose sides measure 62.5mm in length. See Figure 2 below.

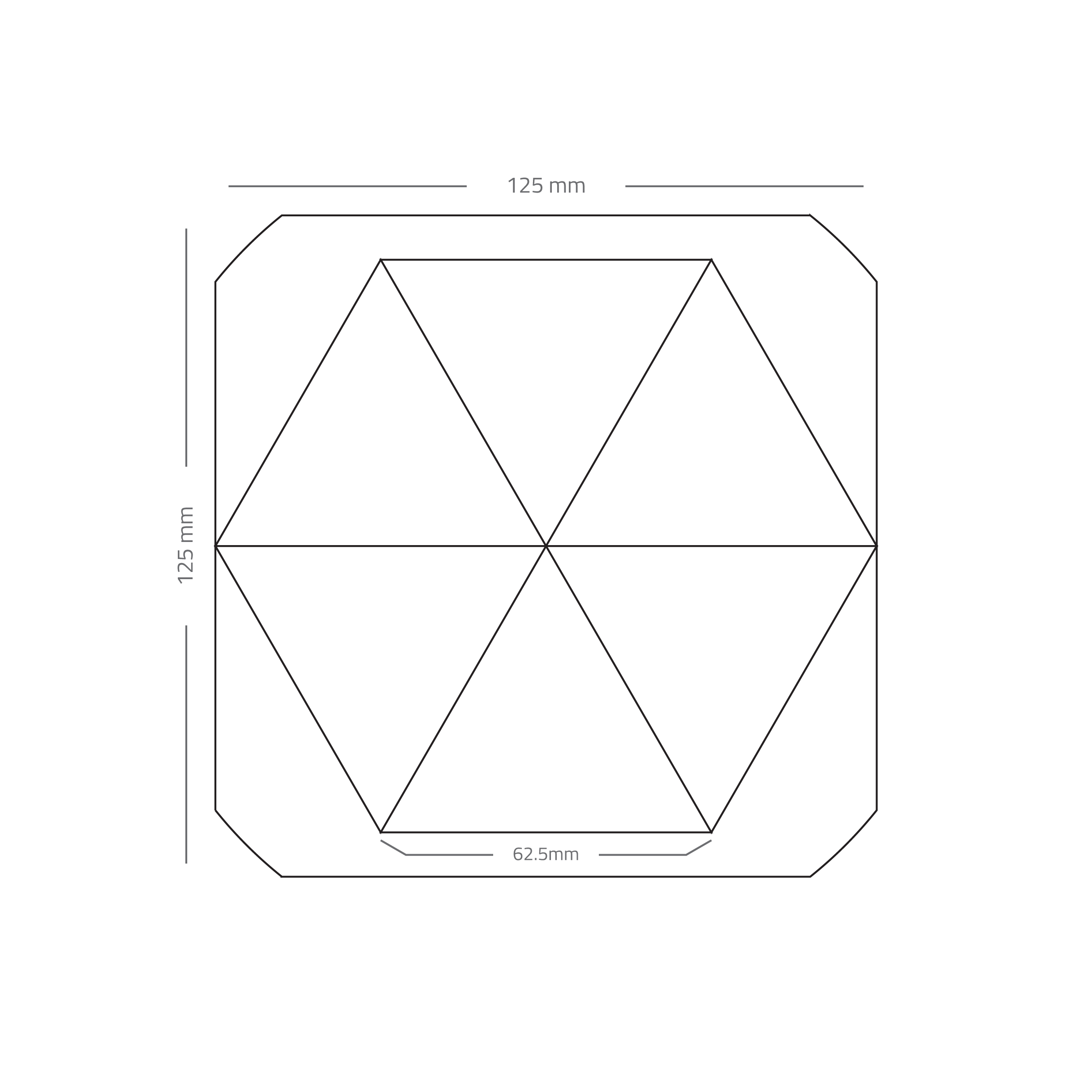
Lets see that hexagon with the actual cell PCB outline (Figure 3)

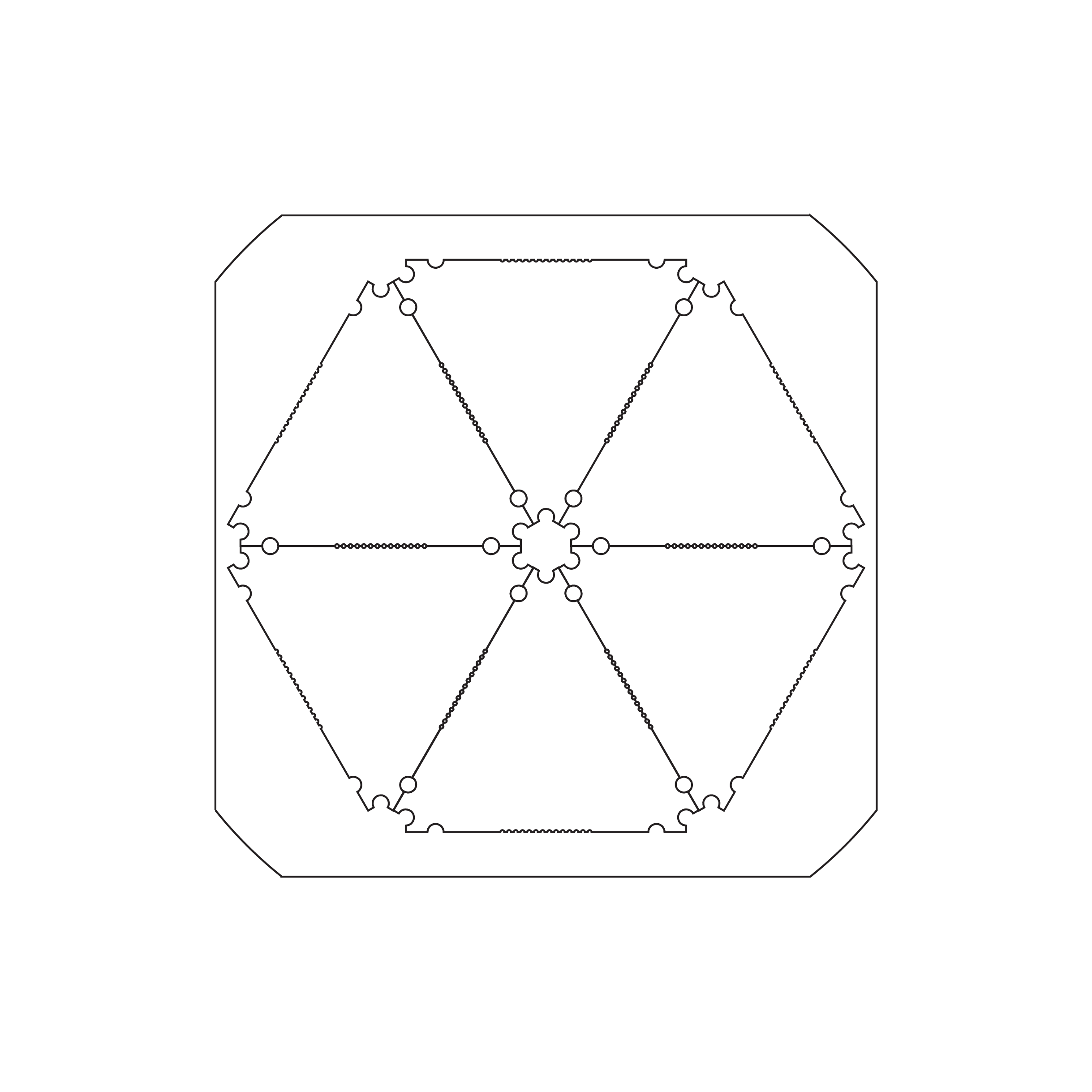
A near perfect fit with just enough room to add some switching circuitry to boost the cell voltage and to hide a beefy battery behind the hexagon assembly.

... The Goldilocks Principle...

When you consider that particular dimension, 62.5mm, that's 2.461 inches which is just enough to design an enclosure whose outside dimensions don't exceed 2.5". Its small enough for portable applications as a single unit or in pairs/triplets. It's just big enough to be used in large numbers without adding too much complexity and does not exceed the available MODBUS addresses (254) to comprise a 1m x 1m array. Among many other things, it all works out!

Not too big... Not too small... Just right.