The basic idea is to increase the positional-resolution of an analog-output encoder by looking for *crossover* between various multiples of the input-signals... E.G. the first obvious crossover to detect is when channel A crosses over its inverse. In the thresholding-sense, this is equivalent to detecting when the sine-wave passes the halfway point. However, detecting *crossovers*, rather than thresholds, results in much better noise and calibration-immunity. Further, more crossovers can be detected than can be accomplished by merely thresholding each of the channels, by e.g. detecting for the crossover between channel A and channel B, or even channel A and -2 * channel B.
So far, anaQuad2x and anaQuad4x achieve 2x and 4x the resolution of a typical digital-output (or digital-thresholded) encoder's 4 steps per slot, giving 8 steps and 16 steps per slot, respectively. anaQuad6x and anaQuad8x are in the works to give 24 steps and 32 steps per slot.
Additionally, this same technique can be used for other locked-phase signals, such as two (of the three) 120-degree hall-effect sensors used on some BLDC motors.
An explanation of anaQuad's functionality follows the videos...
------------------------
(New: 3/11/16: Thoughts on using anaQuad as a communication-method similar maybe to LVDS 4/1/17: More thoughts in the latest log!)
Here's a video of anaQuad running at 4x, with a bit of functional-explanation.
From a 72-slot encoder, 1152 discernible positions can be detected per revolution.
And now, a computer-mouse's encoder, 48 slots -> 768 measurable positions.
This guy's a great (unintentional) test of the system's functionality despite somewhat dramatic calibration-error... The software's configured for a sine wave from 0 to 2.5V, (no software change from the previous experiment) and the encoder's outputting 1V to 3V (whoops), yet seems to be working surprisingly well.
I'm half-tempted to draw up a huge gauge, attach a long needle, and see just how much accuracy/precision I'm actually getting out of this.... and Done:
Maybe at some point I'll hook up my DC motor-positioning software and have a really big dial on the wall indicating something to fractional-degree resolution... (and to test the accuracy of that positioning-software despite things like the "snappy" action of motors intended for speed rather'n positioning, etc.)
An excessively-complicated galvanometer ;)
-----------------
Initial Thoughts: https://hackaday.io/project/9351/log/32010-quadrature-encoders-with-analog-output
Summarized:
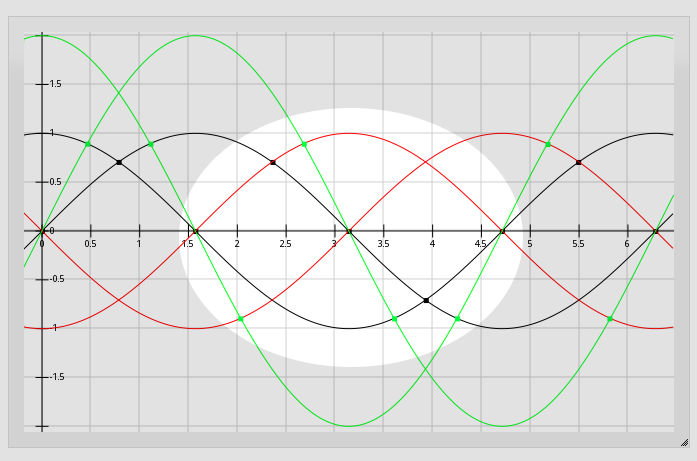
Typically, the somewhat-sinusoidal outputs of the phototransistors are made square via comparators or Schmitt-Triggers.
Thresholding channels A and B
_______ _ A-squared
| | |
| .-¯-. | |
|/ \| |/
-/-------\-------/---
/| |\ /|
A | | '-_-' |
_| |_______|
:. : :
: . 90-degree phase-shift
: . : :
: ._______ : _ B-squared
: | : | : |
: | .-¯-. | : |
: |/ : \| : |/
-----/-------\-------/
: /| : |\ : /|
: B | : | '-_-' |
: _| : |_______|
: : : : : :
: : : : : :
0 1 2 3 0
|<------------->|
One encoder-cycle.
Four Discernible Positions. This method gives four discernible positions for each "slot" on an encoder's disk. So, e.g. if that old ball-mouse had 48 slots around the disk, then it probably measured 192 positions per revolution.An easy way to double that resolution is to look at crossover of the analog waveforms between the channels...
Here
| And Here
v |
.-¯-.-¯-. | A B
/ /:\ \ v / /
-/---/---\---\---/---/
/: /: : :\ :\ /: /
-_-' : : : '-_-'-_-'
: : : : : : :
0 1 : 2 3 : 0
1.5 3.5
|<------------->|
One encoder-cycle.
Six Discernible Positions. And to find the '0.5' and '2.5' positions, merely invert one channel and look for theappropriate crossover.
Crossover-detection is actually quite easy, based on the fact that we're watching every transition; we only need to check for *two* crossovers, rather than all those possible.
HAH!!!
I reversed A and B in this drawing!
(and likely elsewhere)
(A is usually represented by sin(x),
B by cos(x))
~B A B
.-¯-.-¯-.-¯-. ~B A B
B / /:\ /:\ \ / / /
X---/-:-X---\---X---/---/
~B \ /. :/:\: :\ /:\ /: /
A _-'-_-' : '-_-'-_-'-_-'
: . : : : : : : : :
H A B C D E F G H A
Say we're 'at' position A...
So, checking for either H or B...
B: Channel ~B crosses Channel A
H: Channel B crosses Channel A
We don't have to do too much here... knowing which transition happened recently, we look for two other transitions;from position A, it can either go to B or to H, depending on the direction.
From A -> B: channel A crosses the inverse of channel B: So test for A > ~BFrom A -> H: channel A crosses channel B: So test for A < B
From B -> C: cB crosses c~B: B > ~B
From B -> A: cA crosses c~A: A < ~A
... I'll leave the rest to you.
Then we have a switch() statement in an update() function:
switch(lastPhaseState)
{
case PHASESTATE_A:
//Advancing Right to B
if( adcVal_A > INVERT_CHANNEL(adcVal_B) )
{
anaEnc_position++;
lastPhaseState = PHASESTATE_B;
}
//Advancing Left to H
else if( adcVal_A < adcVal_B )
{
anaEnc_position--;
lastPhaseState = PHASESTATE_H;
}
//else, wait here...
break;
//From B -> C: cB crosses c~B: B > ~B
//From B -> A: cA crosses c~A: A < ~A
case PHASESTATE_B:
//Advancing Right to C
if( adcVal_B > INVERT_CHANNEL(adcVal_B) )
{
anaEnc_position++;
lastPhaseState = PHASESTATE_C;
}
//Advancing Left to A
else if( adcVal_A < INVERT_CHANNEL(adcVal_A) )
{
anaEnc_position--;
lastPhaseState = PHASESTATE_A;
}
//else, wait here...
break;
....This system is tested-functional! Woot!
Resolution can be quadrupled by doing a tiny bit of math (this is now functional!).
Click "Read More" for quite a bit more!
 Eric Hertz
Eric Hertz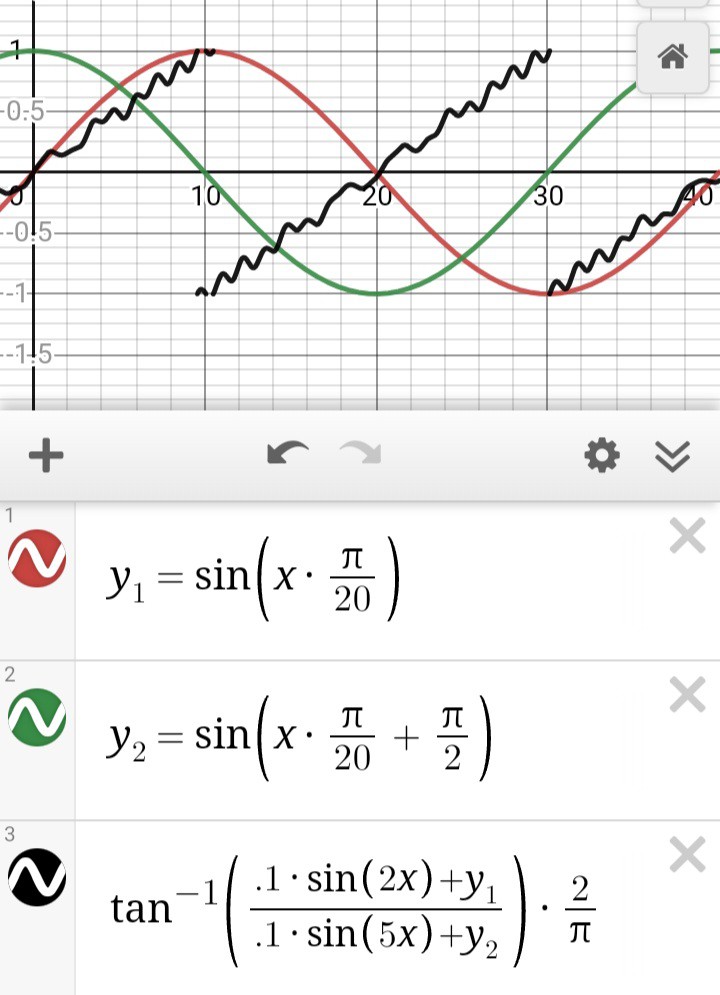
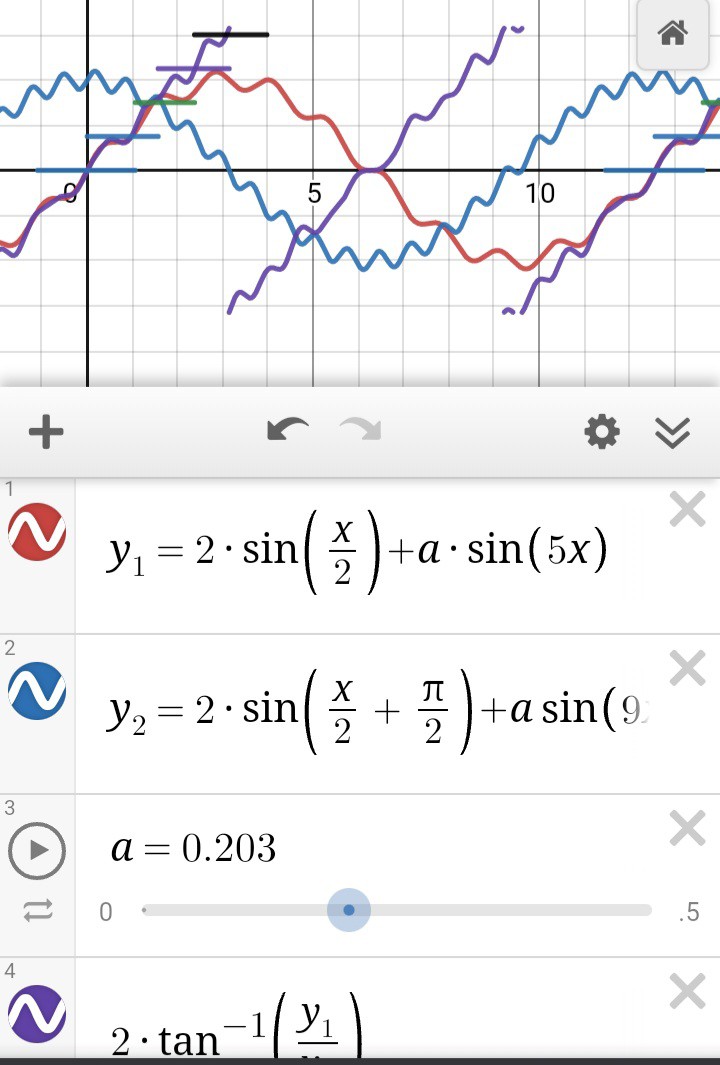
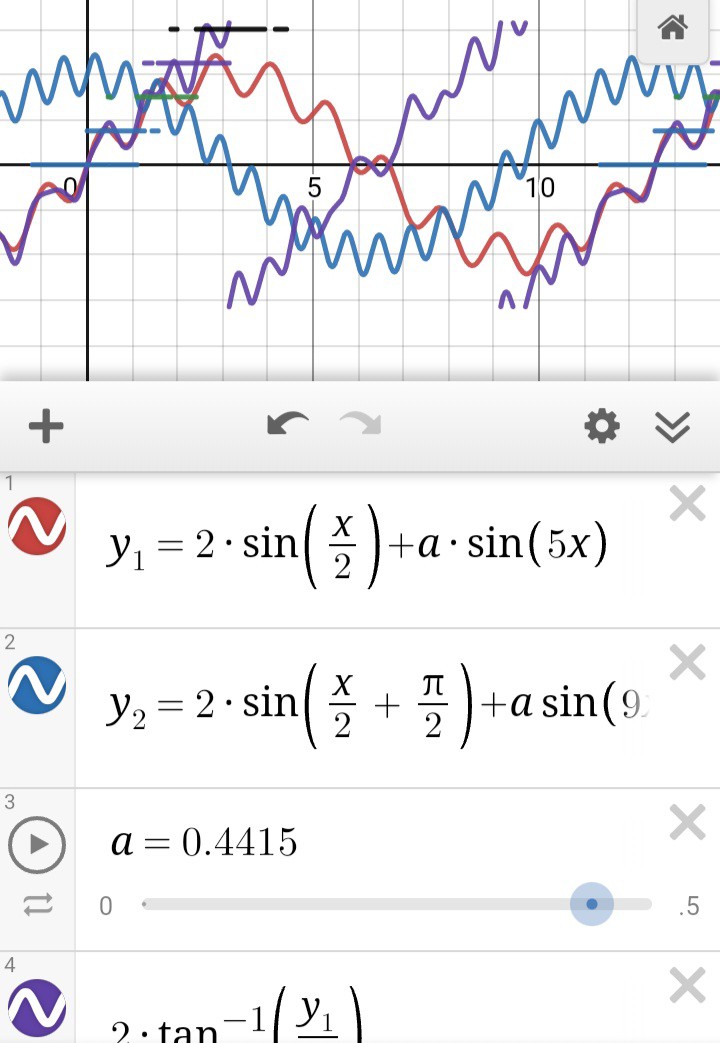


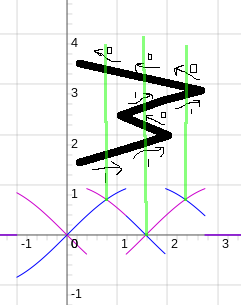 explained below...
explained below...
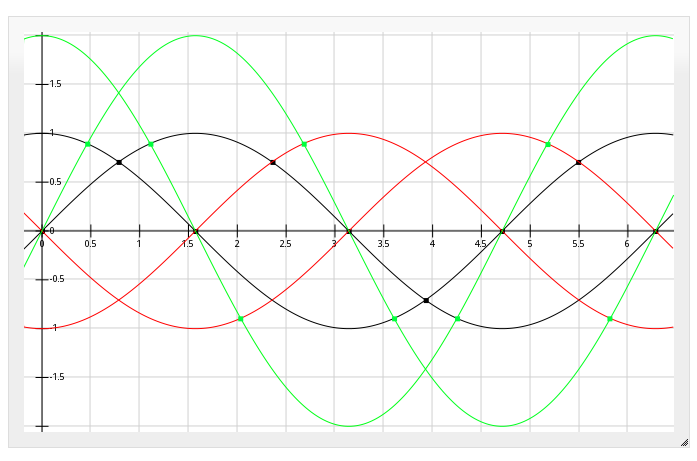

 (
(



 Steven Gann
Steven Gann


I was toying around with your code and I think I have it working with an ALS31313 to measure linear position using.... a refrigerator magnet! The sensor's "common mode" seems to have a nice 90 degree phase between it's X and Z measurements which I pushed into your anaQuad code. The pole pitch of the fridge magnets is ~2mm which should give ~.1mm resoultion. It would make a fairly cheap digital tape measure or DRO. I'm going to mount it with a stepper and ballscrew to see how accurate the measurements are. Have you thought any more about upping the resolution?