UPDATE: Ramblings on LVMDS feasibility/usefulness... why do I do this? See the bottom.
---------
A little more on LVMDS (anaQuad serial-transmission)
 explained below...
explained below...
-----------------
Thought I'd experiment with different graphing-methods... my old go-to online-grapher seems to be down, so here's another:
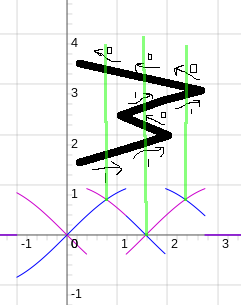
The idea was to show only the crossovers, for a half-period of the quadrature-signal... one half sine-wave, which is the passing of one "slot" in the encoder-disk over the photo-sensor (the other half-sine-wave would be passing of the light-blocking material, which I can't figure out the name for, at the moment... maybe "tooth"?). The other half-sine-wave would be basically the same.
So we have two piecewise-equations:
y1(t) = sin(t) * (t<pi/8) * (t>-1)
+ sin(t) * (t>pi/8) * (t<3*pi/8)
+ sin(t+pi/2) * (t>3*pi/8) * (t<5*pi/8)
+ sin(t) * (t>5*pi/8) * (t<7*pi/8)
y2(t) = -sin(t) * (t<pi/8) * (t>-1)
+ sin(t+pi/2) * (t>pi/8) * (t<3*pi/8)
+ -sin(t+pi/2) * (t>3*pi/8) * (t<5*pi/8)
+ -sin(t+pi/2) * (t>5*pi/8) * (t<7*pi/8)As it stands, I think it's a bit too funky to visualize, the other graphs were more intuitive for me.
But the ultimate goal, here, (which I'd forgotten until I started writing this, having developed these graphs before the ordeal at home weeks ago) is to make it easier to visualize an encoder (or LVMDS) where the speed/direction changes...
E.G. For an encoder-disk, we'd be talking about say a motor slowing to a stop at a specific position. With a poorly-tuned algorithm, it might oscillate around that point due to overshoot. Then, graphing that using the method shown here would allow for a more ideal simulation where speed/position isn't affected by other factors such as the motor's windings or friction. That'd help for explanation-purposes.
E.G.2. For LVMDS, we'd be talking about transmission of data-bits, wherein a "1" would be represented by a clockwise-rotation of one "step" and a "0" would be represented by a counter-clockwise-rotation of a "step."
The latter-case would be much easier to visualize with this sort of graphing technique... E.G. show the transmission of a data-byte in this anaQuad method. So, maybe I'll get there.
As it stands, this graphing program only allows for two plots... so the color-coordination doesn't really make sense... it doesn't correspond to anything in particular, you have to look at the piecewise functions to see what's happening.
Also, this only demonstrates the simplest implementation of anaQuad, which only doubles the resolution of a typical digital-output optical-encoder.
(If this were compared to two LVDS signals, this method doubles the number of bits that can be transferred within one "eye" or one bit-clock, which would be the blue line crossing over the horizontal axis at 0 and PI).
So, maybe I need to write a program to do the graphing... or at least generate the necessary equations.
We'll see.
#Iterative Motion also could benefit from a GUI, so maybe it makes sense to try to refresh myself on OpenGL...
Oh, I have a relatively simple idea for LVMDS... brb.

Also, doesn't show the hysteresis method explained in a previous log, wherein a switch in direction/bit-value would maybe take *two* crossovers to detect, rather than one, just to assure stability, should the electrical-values end-up *near* a crossover, rather than halfway-between.
So, you might be able to see, if there were *two* parallel LVDS signals, their "eyes" would align on the half-sine-wave roughly-outlined in blue. Two data-bits could be transferred simultaneously between 0 and 3.14, one bit on each "signal."
With LVMDS, using two electrically-similar signals as those in LVDS, when those two signals are in quadrature, *four* data-bits can be transferred in the same time, without increasing slew-rates, etc. Something to ponder, anyhow...
---------
So, some pondering, maybe... between the differences of LVDS and LVMDS, at the physics-level... More like rambling...
The frequency-content would be increased... Is that a concern? E.G. the pattern 01010101 sent across LVDS would appear a bit like a sine-wave at a single frequency (half the bit-rate). Whereas, I think, that same pattern over LVMDS would be twice the frequency (but half, or less, amplitude). (right?) (also harder to compare, because it's sent over *two* signals, rather than one).
So, then, there's the question as to whether the frequency-content is a concern... And... we're reaching the limit of my high-speed signal-analysis abilities (especially at this hour and this mind-set). My intuition says that it's less about the frequency-content and more about the slew-rate... that frequency-content analysis of things like the propagation of a signal down a transmission-line is more about a convenient way to look at what's happening... If one were to look at the instantaneous states of things, then consider an instantaneous change, that's more what it's about... (that's how it seems to me).
In which case, especially for this system, maybe we've got to consider not the slew-rate but the slew-rate of the slew-rate? The acceleration-slew?
Another thing to note is that LVDS is designed with proper termination and matched signal-pairs in mind... so, ideally, signal-bounce (reflection) shouldn't be any more a concern for LVMDS than for LVDS. But, we're not in an ideal world... so what effect would reflection have on this system...? On a single differential-pair, probably very little, right? Whatever bounces from one side would bounce in the opposite polarity on the other, and cancel-out at the receiver... right? Hmmm...
Then there's the fact that in this system *two* pairs must work in unison... Reflection on one pair would *not* be coupled into the second, and thus *not* cancelled out... Hmmm...
Then there's jitter and skew... Whereas two LVDS (or even two *parallel*) data-signals could arrive at their destinations, say, 4 picoseconds apart, and still be considered valid, with this system we might need increased precision in that regard... 4ps skew tolerance for LVDS, 2ps for LVMDS. Oy.
What's the effect...? Well, jitter's a bit more difficult, so let's look at skew... That's pretty easy, just imagine that one wire-pair is 2ps longer than the other. I think the rule-of-thumb is 6inches per nanosecond, so 1ps would be 6/1000inches = 0.006in? 6 mils? Kinda tight tolerances for a couple wire-pairs! (And, thus, the reason why we've moved from Parallel ATA and Parallel PCI, and so-forth, to Serial-ATA and PCI-Express, etc.)
That's a pretty big one, right there. Hmmm...
OTOH, maybe, instead of thinking of this as a way to send twice the information at current speeds, instead think of it as a way to send the same amount of information at half the speed?
........
Here's a ponderance... does LVMDS need to have two differential-pairs? Could the same be accomplished by a single pair, where one wire carries the A signal and the other carries B? Since *crossover* is the concern, rather than *value*, maybe coupling these two 90-degree out-of-phase signals *as though* they're differential (and 180deg out of phase) would still gain some of the benefits of a normal differential pair. External electrical-noise coupled into one wire would *also* be coupled into the other wire... So, a common-mode voltage is introduced... and may not matter. (or may...), because, again, we're concerned about *crossovers*.
(Then again, one of the important crossovers to be detected is that of a signal and its inverse, which is part of the reason two differential pairs made sense).
And coupling *between* the signals...? hmmm...
And signal-bounce...? oy...
Anyways, the concept of LVMDS was just a groovy idea I had a while back... based on anaQuad which is nothing to do with anything other than quadrature encoders with analog outputs. No idea whether there's any use for LVMDS in an era where even LVDS is likely somewhat outdated. (Surely your SerialATA cable isn't made with wire-length tolerances of 6mils, right?!)
 Eric Hertz
Eric Hertz
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.