I'm working on a new circuit (really!), but did these calculations last night, and thought the results were interesting.
LED datasheets often quote the luminous flux in lumens, based on the daytime visual sensitivity curve (photopic vision). This is calculated by integrating the LEDs spectral radiant flux with the photopic luminosity function, and reflects how bright the LED appears to daytime-adapted eyes. For nighttime marker use, we are interested in "scotopic lumens" which would more accurately measure how bright the LEDs look to dark-adapted eyes. I scraped the LED spectral curves from the datasheet and with some numeric manipulation in an octave script, calculated the scotopic luminous flux for the three Luxeon Z LEDs I have been looking at:
| Color | Photopic Lumens (datasheet) | Scotopic Lumens (calculated) | lm/W (photopic) | lm/W (scotopic) | Electrical Power (W) |
| Cyan (LXZ1-PE01) | 68 | 782 |
46 | 528 |
1.48 |
| Green (LXZ1-PM01) | 108 | 618 |
71 | 407 |
1.52 |
| Lime (LXZ1-PX01) | 199 | 642 |
142 | 459 |
1.4 |
The datasheet lists the output at 500 mA, so I multiplied by the forward voltage (from datasheet curves) for each of the LEDs to get the input power.
The lm/W (electrical watts) columns in the table are the most interesting. For true dark-adapted vision (like in a cave or really good astronomy site), the cyan LED wins at 528 lm/W - but, this LED is poor for daytime vision. During the day, the lime LED is far superior to either of the others at 142 lm/W - and it takes a close second place behind the cyan at night. If you're making a glow marker and want it to be generally useful in all lighting conditions, the lime LED seems like the best choice. The only downside: it costs $4.20 vs $2.76 for the others. The marketing department over at Lumileds has their act together.
Details
Here's how I calculated the values in the table. Math and/or photometry nerds may want to check my approach; others may feel the desire to skip this entirely :-)
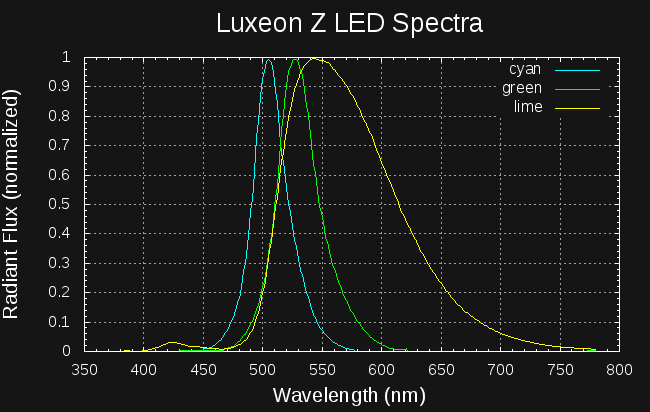
The datasheet provides the photopic luminous flux (in lumens) and a normalized spectrum for each LED. I digitized the spectra with Engauge Digitizer, shown replotted on the same graph here:
The datasheet lists the photopic luminous flux, , for each LED in lm. This is calculated by weighting the spectral flux,
, by the dimensionless photopic luminosity function,
:
To calculate an analogous scotopic luminous flux,
,we can perform the same integration, this time weighting by the scotopic luminosity function,
:
This would be straightforward, except that the spectral flux isn't given directly in the datasheet. However, we can calculate the spectral flux from the given luminous flux and the dimensionless (normalized) LED output spectrum, which I'll call . The spectral flux is proportional to the normalized spectrum:
Substituting this, we can solve for the constant C:
and then evaluate the scotopic luminous flux:
The raw data files and the octave script I used to perform these calculations can be downloaded here.
Update: writing this log revealed a scaling error in the original octave code; I've re-run the numbers and updated the code and table.
 Ted Yapo
Ted Yapo
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.