Before I begin, I need to point out that this log follows after My Introduction to Linear Programming and GPLK. So, any explanation having to do with why I'm adding logs on flow network problems and references to the topics, I will either skim over or entirely avoid here! But, the relevant take away from the previous log is that I've been teaching myself the many ways Maximum Flow ( MFP ) and related problems can be solved, which lead me to the Linear Programming ( LP ) optimization with GNU MathProg ( GMPL ) and its C API, the GNU Linear Programming Kit ( GLPK ).
However, even though I find GMPL to have the most intuitive syntax, I find there are a lot of limitations with GMPL! The GLPK API is nice in that I get to use the language I'm most familiar with, but the API forces the user to always formulate their problem in the standard LP form. This leads me to the focus of this post.
The Idea: Learn how to solve Maximum Flow Problems in MATLAB and LEMON ( C++ )
The tools that sparked my interest the most are MATLAB, LEMON, and Boost Graph Library ( BGL ). MATLAB, to me is the most convenient language / development environment when it comes to reducing the time it takes to write the code! Heck, it has carried me throughput my years as an undergraduate and also as a graduate. But, I actually have more experience in C++, and so I decided to look into two possible graphing libraries. From what I can gather, two of the most well known graphing libraries are LEMON and BGL, and for a moment I was really tempted to go with the latter. But, a comment on stack overflow suggested I may run into issues with the documentation. I should point out that comment was posted back in 2011. So, there's a good chance BGL is better documented today. In the end I decided to learn LEMON over BGL, based primarily on how intuitive the libraries are to understand.
First and Second Implementations: MCFP-CF Solved with MATLAB and LEMON
Basically spent part of last week and a lot of the weekend reading through documentation and implementing my own examples, for both MATLAB and LEMON. In this log, I present three of those examples. The first two solve the same Concurrent-Flow variant of the Multi-Commodity Flow Problem ( MCFP-CF ) with LP, as was done in the previous log. However, in this log I do a MATLAB and C++ implementation.
For those who don't already know, MATLAB allows for dynamic access to the members of a structure. Effectively, this is how MATLAB implements associative arrays ( e.g. Python Dictionaries, C++ map class, etc. ). Not sure of its performance, but it can make very nasty looking code look a lot less nasty. Unfortunately, the first time I wrote the MATLAB implementation, I COMPLETELY forgot MATLAB could do this, and as a result, ended up with so many undesirable for-loops, something to be avoided in MATLAB. The second revision, whose MATLAB source code can be found here, is a lot cleaner! Granted, it probably runs poorly since I focused on making the code readable rather than efficient.
The C++ implementation can be found here. I should point, LEMON doesn't do any of the LP itself. Instead, it interfaces to other solvers. In my case, it just defaults to GLPK! Compared to the MATLAB implementation, the C++ solution is a lot longer in terms of number of lines, excluding comments and declarations! And, even after becoming familiar with the LEMON library, it definitely took more time to write the C++ implementation! But, C++/C solutions seem more prevalent in NoC-related research ( that I've looked at ), probably because of the gains in performance. The C++ implementation is also more accessible to people, since anyone can freely download the compilation tools and the required libraries.
Third Implementation: MCFP-CF Solved with Iterative Solution with LEMON
This final example solves the same MCFP-CF, but with a slightly different approach. The idea behind algorithm I actually got from this dissertation. Before I jump into any details, the full source code can be found here, which does include documentation on pretty much what I'm going to explain here.
With any good explanation on a mathematical algorithm, it's always a good idea to define all nomenclature --- even if the algorithm is simple and/or the nomenclature is somewhat obvious ( in my opinion, I should add ). So, like in the last post, the network has the following form.

An important step in the algorithm is to solve the Maximum Flow Problem ( MFP ) for a given commodity and the graph.
Cheers!
 andrew.powell
andrew.powell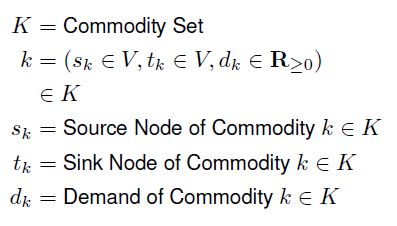
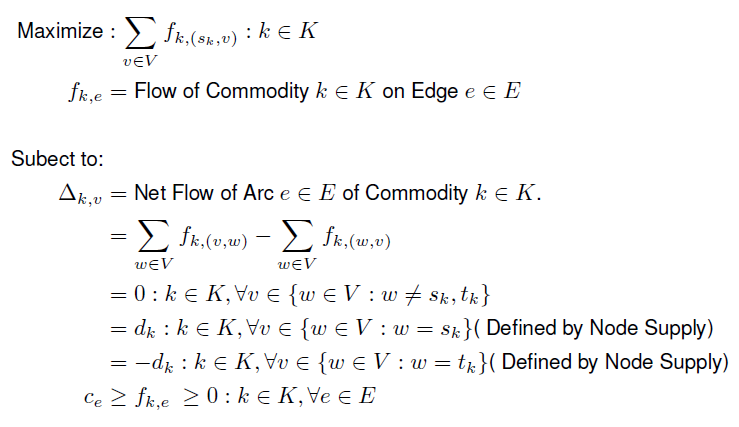

Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.