So, creating a good sounding square wave digital oscillator is easy — just send a bunch of zeros followed by bunch of ones (where "bunch" is related to note frequency). After all, it's just a square wave with two alternating values. Well, not exactly...
When working in digital domain (sampled signals) we have one limitation known as Nyquist-Shannon sampling theorem which states that sampling frequency has to be at least two times higher than maximum frequency contained in signal (it should be even higher for better reconstruction). And the same limitation exists both when sampling input signal and when converting digital signal to analog.
What exactly happens if signal contains frequencies higher than half of the sampling frequency? It's called aliasing — frequencies higher than half the sampling frequency appear as f-fs signal which can be used for some interesting effects (https://www.youtube.com/watch?v=uENITui5_jU) but usually we don't want it. Especially when creating oscillators.
So, what to do? Easy, remove (or don't include) everything above fs/2 before D/A or A/D conversion.
When sampling analog signal an external anti-aliasing filter is required in front of ADC.
But when synthesizing, we can immediately create signal which will not alias (in reality not that easy, especially if we have some saturators or non-linear elements).
By using Fourier analysis, every signal can be decomposed as a sum of sine and cosine signals (partials) with frequencies which are multiples of base frequency. So, if we want to create square wave signal which contains fs/2 at most then we'll sum all the partials up until that frequency. And that is called band limited synthesis.
In this project I'll be using wavetable oscillators (signal shape is saved in a table and played at the desired frequency). Good oscillator would use multiple tables (at least one per octave) but I just want to get something working so there will be only one table. So, when highest available note/frequency is played by oscillator it mustn't contain any partials above fs/2. Downside of this (using only one table)) is that for low notes we have quite a lot of "unused space" in spectrum and it sounds a bit dull without additional higher frequency components — a thing that can (will, at some point) easily be fixed with additional tables, each for one range of frequencies.
For this I've written simple Jupyter notebook which can calculate the tables and plot the signal shape (can be found in data/bandlimited_waveforms.ipynb in Git repository).
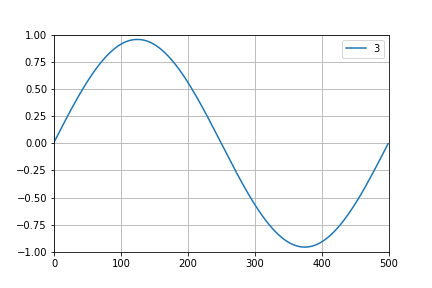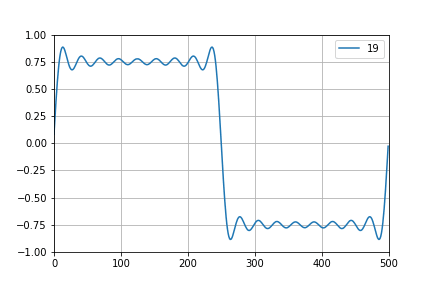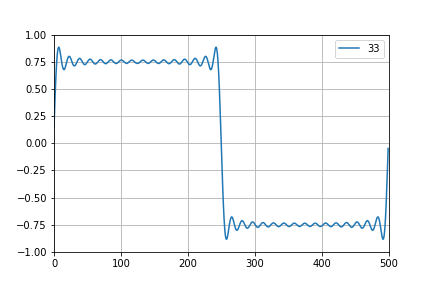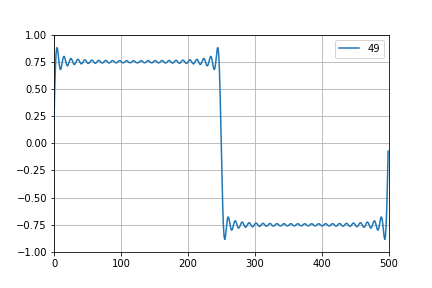
 Igor Brkic
Igor Brkic
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.