Introduction
Concorde is a cut and branch based exact TSP solver. In other words, the solution from Concorde is the best optimal solution among all feasible one.
However, due to license constraint (see the last license issue section for details), I have to look into an alternative heuristic (approximation) approach later.
Build Concorde
1. Download Concorde source code from here.
2. Download a binary LP solver from here and deploy the header and static library into ./QS64_linux or ./QS64_darwin sub folder under Concorde source code depending on your platform.
3. Build with the following script:
if [ "$1" == "linux" ];
then
echo "Build for Linux 64"
make clean
./configure --with-qsopt=$PWD/QS64_linux
make -j 16
elif [ "$1" == "darwin" ];
then
echo "Build for Mac OS X 64"
make clean
./configure --with-qsopt=$PWD/QS64_darwin --host=intel-x86-linux
make -j 16
else
echo "Unkown parameters!"
echo "./build-64.sh [linux|darwin]"
fi
4. If you resolve all other dependencies in your build platform and build it successfully, Concorde binary will reside in ./TSP folder.
PoC
Given entry points and exit points of each part in the layer from output text file, we can use asymmetric traveling salesman problem (ATSP) solver to find out the optimal traveling order of the parts such that air time travel distance is minimal.
If you already build and \play with Concorde, you will find that Concorde seem to only solve TSP, where there is one and only one weighted edge between two vertexes. I have to say Concorde is great except its poor documentation. For last 10 years, its developer's guide is still under construction. You can hardly find a user guide to tell you how to provide input and interpret output.
In any rate, Concorde is free. So stop complaining and poke around this.
After reading its test code, it mentioned TSPLIB, which is TSP solver benchmark data. Google TSPLIB and you will find its data format. I shared the data format specs in the file section. There are two ways to define edge weight in TSP:
1. Define vertex coordinate -- Vertex_Index X_coordinate Y_coordinate.
2. Define edge weight matrix. If the matrix is not symmetric, you turn Concorde from solving TSP into ATSP
See TSPLIB tsp input data here.
So I manually write a trivial case to do a PoC. See the diagram below generated by dot file and the in and out of Concorde.
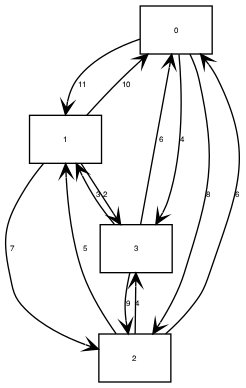
TSPLIB format input:
Ricky@imac:~/repo/concorde/SAMPLES$ cat 4point.tsp
NAME: demo
TYPE: TSP
COMMENT: 4 vertexes asymmetric problem
DIMENSION: 4
EDGE_WEIGHT_TYPE: EXPLICIT
EDGE_WEIGHT_FORMAT: FULL_MATRIX
EDGE_WEIGHT_SECTION
9999 11 8 4
10 9999 7 2
6 5 9999 4
6 3 9 9999
EOF
Concorde output:
Ricky@imac:~/repo/concorde/TSP$ ./concorde ../SAMPLES/4point.tsp
./concorde ../SAMPLES/4point.tsp
Host: imac Current process id: 96043
Using random seed 1528799254
Problem Name: demo
Problem Type: TSP
4 vertexes asymmetric problem
Number of Nodes: 4
Explicit Lengths (CC_MATRIXNORM)
Optimal Solution: 21.00
Total Running Time: 0.00 (seconds)
Ricky@imac:~/repo/concorde/TSP$ cat 4point.sol
4
0 2 1 3
Concorde deliver the optimal tour 0 => 2 => 1 => 3 => 0 with optimal cost 21.
For our path planning purpose, we don't need a tour that comes back to the original point. One trick I made is to add a facilitated vertex where its in and out edge weight is zero and connect to all other vertexes.
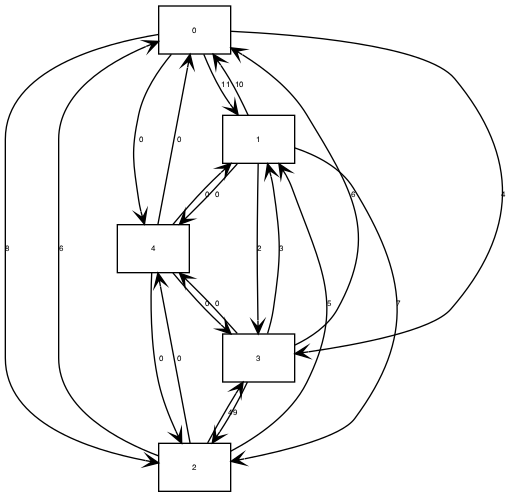
Augmented Concorde Input:
Ricky@imac:~/repo/concorde/SAMPLES$ cat 4point_extended.tsp
NAME: demo
TYPE: TSP
COMMENT: 4 vertexes asymmetric problem
DIMENSION: 5
EDGE_WEIGHT_TYPE: EXPLICIT
EDGE_WEIGHT_FORMAT: FULL_MATRIX
EDGE_WEIGHT_SECTION
9999 11 8 4 0
10 9999 7 2 0
6 5 9999 4 0
6 3 9 9999 0
0 0 0 0 9999
EOF
Augmented Concorde Output:
Ricky@imac:~/repo/concorde/TSP$ ./concorde ../SAMPLES/4point_extended.tsp
./concorde ../SAMPLES/4point_extended.tsp
Host: imac Current process id: 97242
Using random seed 1528804704
Problem Name: demo
Problem Type: TSP
4 vertexes asymmetric problem
Number of Nodes: 5
Explicit Lengths (CC_MATRIXNORM)
Optimal Solution: 13.00
Total Running Time: 0.00 (seconds)
Ricky@imac:~/repo/concorde/TSP$ cat 4point_extended.sol
5
0 4 2 1 3
By removing the facilitated vertex 4, we got a path 2 => 1 => 3 => 0 with optimal cost 13.
Converter
Writing a converter is a piece of cake in Python. We have X and Y coordinate of all entry point and exit point of parts. Compute its Euclidian distance, generate the asymmetric weight matrix and then add a facilitated vertex. Then our converter is done.
[Work-in-progress]
License Issue
I shoot an email to Prof William Cook, who owns Concorde and co-authors the great TSP book, and ask if I can use Concorde under GPL. He suggest to make use of Concorde as my hobby project, instead of GPL. I respect that. After reviewing Concorde source code, you will be amazed how many years of experience and intelligence built in that implementation.
I don't think I have bandwidth or enough intelligence to build a TSP solver from ground up. He pointed me to implement TSP in a simple heuristic approach -- 3-opt (k-opt) approach. I will look into that as I'm writing this log.
 Ricky Zhang
Ricky Zhang
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Very thank you!
Are you sure? yes | no
How do you feed the asymmetric weight matrix to Concorde?
Are you sure? yes | no
Hey Madhi, from my understanding you need to transform your ATSP to a TSP problem. A method that keeps the optimality doubles the number of nodes
Are you sure? yes | no
[this comment has been deleted]
No, you only described the topology of some vertexes the way you did it. It is not even complete. You either describe the edge matrix with its weight as the matrix element value or you use vertex coordinate method where record the vertex in (x, y) 2D coordinate.
Are you sure? yes | no
I'd recommend you using the edge weight matrix to describe them. For example, if two vertexes are NOT connected, the weight is large value like 999999. If two vertexes are connected, the weight is 1. Since, they are bi-directional and the weight are the same, the edge weight matrix is a symmetric matrix.
Are you sure? yes | no