Optimisation of the Original MPRT
So okay, I decided to see if I could optimise the original MPRT.
Not a trivial task, but doable with brute force:
- For each Pressure Angle (PA) from 15 degrees to 25 degrees in steps of 1 degree.
- For each Diametral Pitch (PD) from 0.75 to 1.25 in 0.05 steps.
- Test for interference for 1/10 rotations of the tooth.
Test for interference?
Basically test if any points from the external gear are inside the planet gear.
Okay, the results suggest any PA between 20 and 25 degrees is okay, and for the original MPRT configuration (18/21/-60 & 21/-57) the optimal DP for the output ring is 94.0% of the PD of the drive gear set.
But like most code you do have check the results, so for each 1/10 tooth rotation of the optimal result, DXFs were export and checked.
Now, at least to me, the gears are meshed (no backlash) but the contact is between the outer teeth, not the centre tooth (see image below):
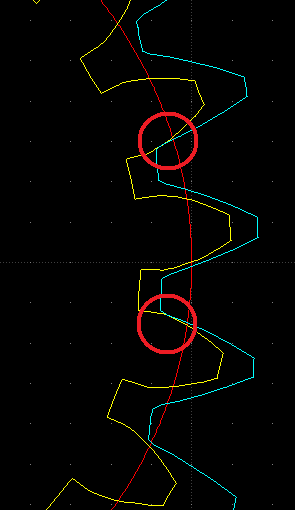
All the other 1/10 tooth rotations are similar.
The next rabbit hole?
The contact area is mostly on the low area of the planet and high area of the ring. These are not important areas (I think?) for normally meshed gears. The meshing may be improved by trimming the high area of the ring gear.
Ideally the pitch circle of the planet and the ring gear should touch (the red and green circles):
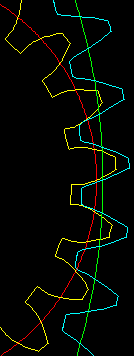
So the plan would be to set the ring gear pitch circle to touch the planet pitch circle, and then "trim" the ring gear top of tooth area until there is no interference (for 1/10 tooth rotations).
Need to work out how to code "trim". Hopefully an easy fix for the Make Gear code pops out of the experimentation.
Results or Any Easter Eggs?
After a long day hacking my code, here is a solution:
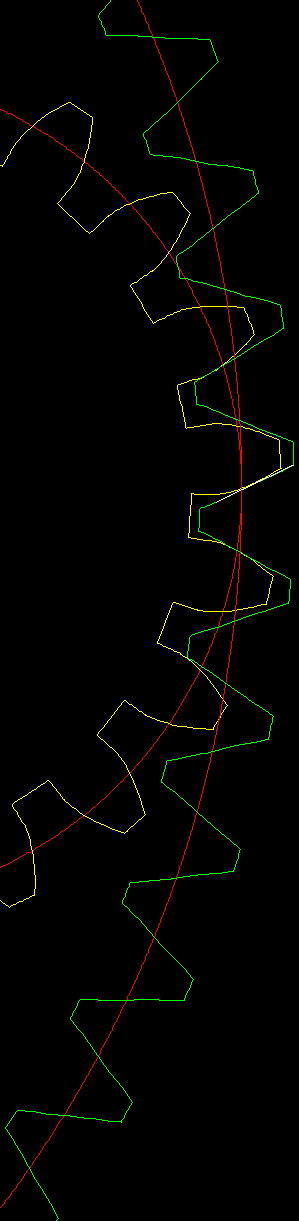
Note the white line. It is to show how straight the tooth profile.
Optimality?
Now, is it optimal, can I do better? What are the results telling me?
And the answer is not "42" as it has 57 teeth!
Like usual I have to sleep on it.
The Answer
The answer is that the gear pitch circles are not valid!
- As the gear is locked it has to rotate 57 to 21, and the gear pitch circles are not in this ratio (as their Diametric Pitch (DP) are different).
- The effective pitch circles have to be 57 to 21.
- So the teeth have to contact either side of the centre, where the effective pitch circles must overlap or cross.
For tooth clearance purposes, using the gear pitch circles for gear design is appropriate.
So in conclusion, the design is now fully constrained and zero backlash, optimal by our definition.
Note, as I trim gear teeth for interference, the pressure angle is no longer important.
Universal Epicycle Gear Formula
I found the universal epicyclic gear formula:
- Tc*(Ns+Nr)=Ts*Ns+Tr*Nr
Okay, I rearranged it a little to suit my tastes.
- Ts = Turns in the Sun
- Tc = Turns in the Carrier
- Tr = Turns in the Ring
Note: The Planets play not role
- Ns = Number of teeth on the Sun
- Nr = Number of teeth on the Ring
Basically, you set Ns and Nr, and two of the three Ts, Tc and Tr, and solve for the unknown.
Let's try Daren's design:
- Ns=18
- Np=21
- Nr=60
Note: Nr=Ns+2*Np
- Ts=1 (one turn)
- Tr=0 (fixed)
Therefore:
- Tc=(Ts*Ns+Tr*Nr)/(Ns+Nr)
- Tc=(1*18+0*60)/(18+60)
- Tc=18/78 (=1/4.333)
Next Stage:
- Ns=18
- Np=21
- Nr=57
- Ts=1 (one turn)
- Tc=18/78
- Tr=(Tc*(Ns+Nr)-Ts*Ns)/Nr
- Tr=(18/78*(18+57)-1*18)/57
- Tr=(18*75/78-18)/57
- Tr=-0.01214575 =(-1/82.333)
A reduction ratio of -82.333 was the previous calculation.
AlanX
 agp.cooper
agp.cooper
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
'Calculation' is a strong word. I guessed. :)
It was a logical guess though.
The first stage planetary is 18/60, so that gives a 3.3:1 ratio, and the second stage would move 3 teeth per revolution of the first stage. 60 teeth in the second stage, so that would take 20 revolutions of the planets to move *a little more* than a full revolution. Hence my estimate of ~66.6:1.
Are you sure? yes | no
Thank you again @agp.cooper . I'm trying to work out how to duplicate what you did here within OpenSCAD.... The individual involute teeth are built with polylines now, so I suppose I could just modify one tooth within that space, and then use it normally. Determining the polyline required, dynamically, that's a whole other ball game though. It's going to be hella complicated as both the target and meshing gear sizes alter the resulting tooth profile.
I could do what you did here and just rotate/subtract/rotate/subtract but I think my time would be better spent pursuing the inherently perfect version. I think I'll do that first, and if I have time to come back to this, I will.
Are you sure? yes | no
1) Yes, the OpenSCAD way is probably "rotate (the planet) and cut (the internal)". The rotation is a fraction of a tooth rather than degrees/radians.
2) May be better off using the polyline produced by my code and importing it into OpenSCAD.
3) The third option is to develop the relationship between the pressure angle, number of teeth for the gears, and the angle of the "straight" line developed by the "rotate and cut process".
4) There may be an easy relationship or may be not. The worst case is you develop some regressions. It looks like about one or two days to generate a set of regressions.
---
The best option is if you can get OpenSCAD to rotate and cut as this would be useful for developing other gear profiles and normal gears without interference.
---
Spent the day putting in garden reticulation for my partner. So pretty tired.
AlanX
Are you sure? yes | no
I appreciate you going down these rabbit holes and letting us all know what they look like from down there!
Are you sure? yes | no
So do I! I'm kind of in the the camp that @agp.cooper has already found a better solution though. This research could be useful in it's own right, but I personally am going to run with that. (split planets and perfectly matching gear ratios). The only downside to his approach that I can see, is it adds a resulting rotational force to the planets which may need to be countered by having a carrier for them. Still, by far, the most prodigious contributor to a project I have ever had with the possible exception of @Morning.Star . A round of applause please.....
Are you sure? yes | no