 Ho ho ho! Here we go again! : )
Ho ho ho! Here we go again! : )
Do you remember my promise to come back if I would manage to develop charge-based electromagnet? Well, I failed with that, I can't solve this riddle, but... I have a mind-blowing alternative!
This would be a long story, so I am gonna describe what I achieved in couple of words for readers not familiar with electricity and then I'm gonna head towards details and sort of theoretical explanation.
Core problem of electromagnetic actuators (and all electromagnetic devices) is heating - it limits power/mass ratio and wastes precious energy onto something you don't generally need. In a situation when magnetic field isn't performing any work it's especially ridiculous.
In previous logs I noticed, that dissipation isn't an attribute of current in a several case, but this case cannot close the circle alone: it was true only during discharge of a magnetic field. Before that I discovered, that voltage at some extent can reduce dissipation and started to develop a control circuit, which can operate under high voltages. High voltage is a real trouble to deal with!
Briefly speaking, greater voltage can charge coil faster. But is it the only way to do that? No.
You can hack a resistance itself. Superconductivity allows you to get very strong fields, this method also does. Later it can be used for transformers, drone engines, precision machines (to minimize thermal expansion) and, of course, it makes my "artificial muscles" possible : )
Theoretical explanation and details
Previous theoretical parts:
Part one
Part two
1. Possible source of heat dissipation
As we found, you can get current without a heat, traditional "frictional" explanation doesn't seem so fair. We know what voltage can be a result of a potential difference and "potential difference" redefined - difference in energies. Electrons flow from greater potential (-) to a lower potential (+)
So... Energy drops! And where it goes? Maybe into heat. P=U*I, where U is energetic difference and I is amount of charge, which goes through that difference every second. Similarly, E = U*I*t, where I*t is an amount of charges which went through that difference overall.
Let's consider three situations:
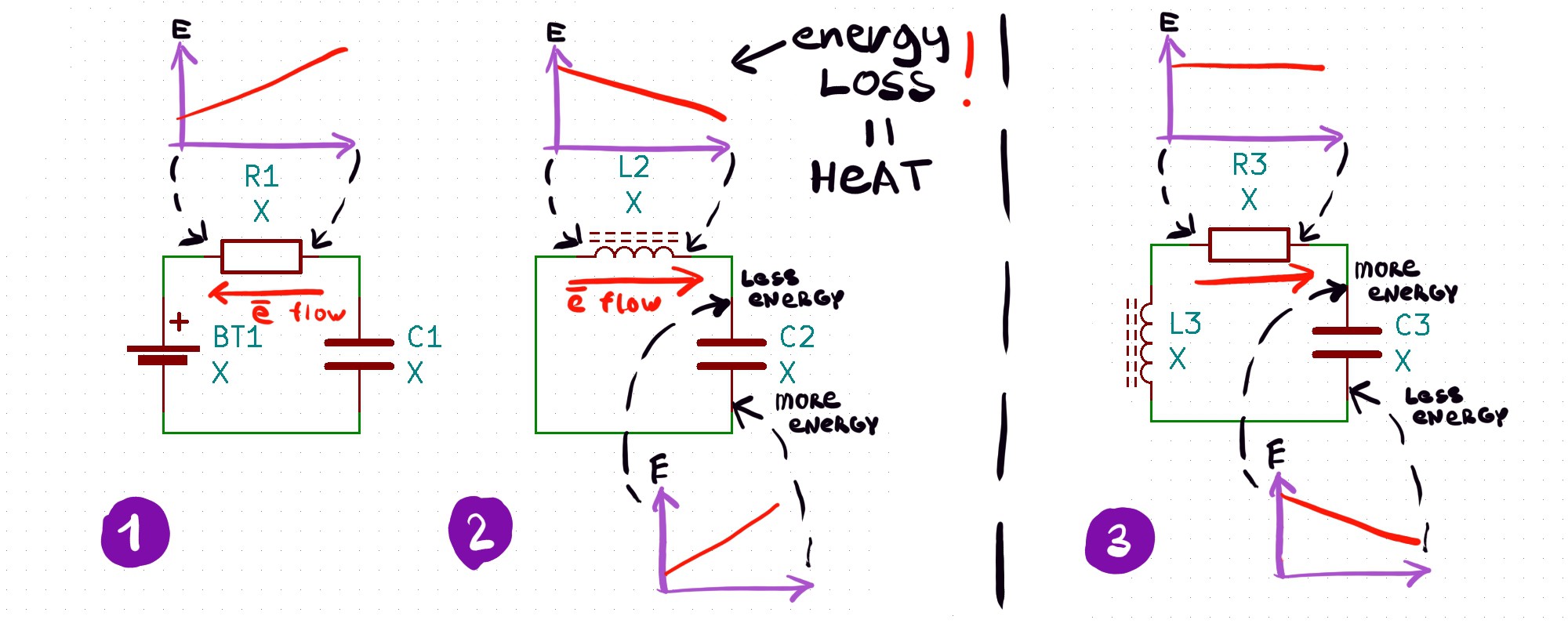 First one is a typical situation with a resistance, voltage drop on which represents potential difference.
First one is a typical situation with a resistance, voltage drop on which represents potential difference.
Second one is a discharge of a capacitor onto coil, where potential difference produced by a capacitor.
Third one is interesting one, as coil never takes voltage into account, only current, it would try to produce enough voltage to maintain flow of electrons, so voltage on a coil stays equal to voltage on a capacitor. There are still a lot of questions about this one, but it's the one with virtually no heating at all.
> > > > > > Disclaimer! Next part is a wrong assumption! Left it there just for history : )
2. Boosting a field-charging process
To generate electromagnetic field we should achieve surface charge gradient (according to a first theoretical part) and it seems that this gradient is tightly bounded with current & voltage. But as we have a "perfect" discharging cycle which takes some time (this was in a second theoretical part), we can try to speed-up charging process that much, what it wouldn't dissipate much energy and efficiency would be close to 100%.
There are two ways how we can move charges - non-insulated way, like we always do by attachment of power supply or a capacitor and external field way - insulated. Best way to generate external field is by a capacitor. Fun part - external fields never bothered by internal circumstances! And resistance is one of that circumstances. That's how we swap resistances here!
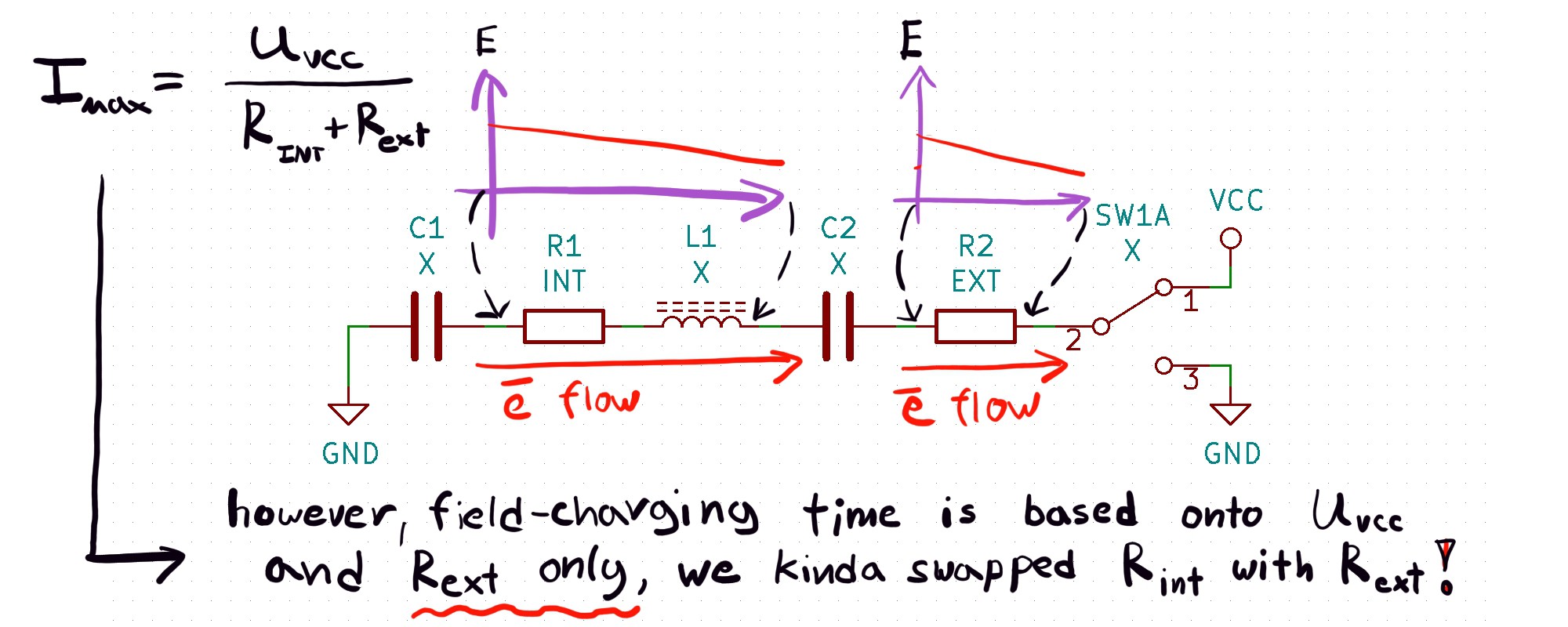 Elegant, easy, all our problems with charging solved. Experimental setup was also simple:
Elegant, easy, all our problems with charging solved. Experimental setup was also simple:

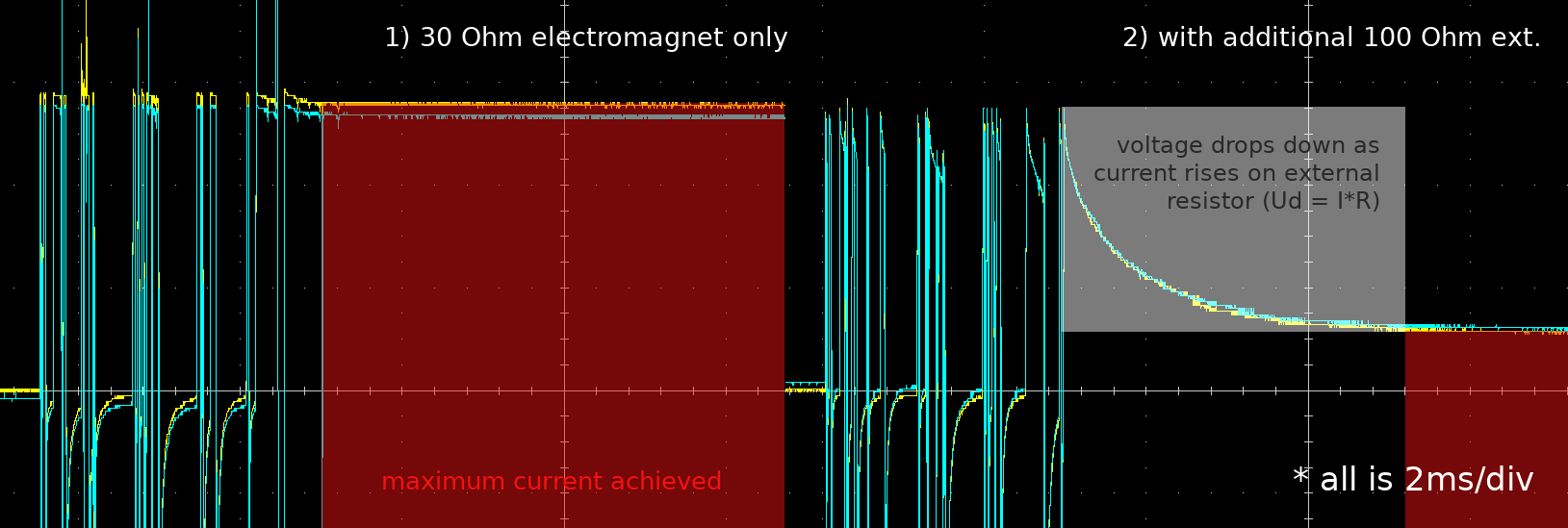 Significant improvement. Voltage drop on external circuit resistance is very helpful, since we can determine when current is on the right level and when charging process ended. If curious - this electromagnet charges for about 16ms attached to a power supply, 40x times slower than here!
Significant improvement. Voltage drop on external circuit resistance is very helpful, since we can determine when current is on the right level and when charging process ended. If curious - this electromagnet charges for about 16ms attached to a power supply, 40x times slower than here!
I simulated this process using methods from first theoretical part, worked just fine:
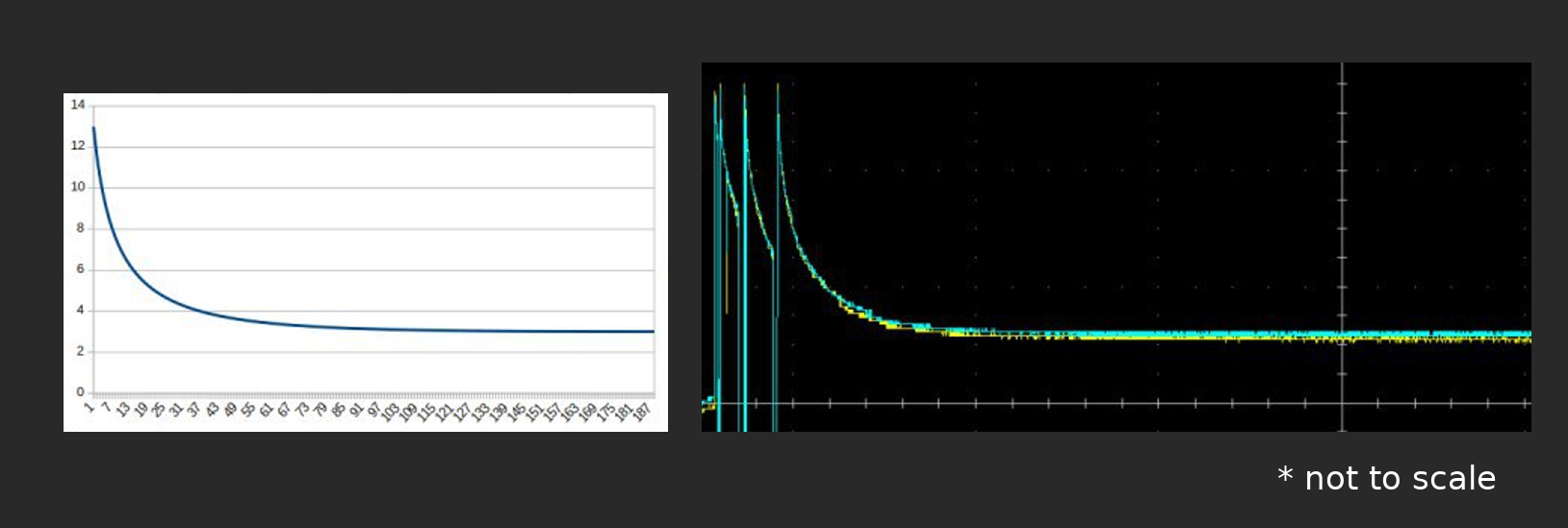 As a conclusion: resistance swap rules! : ) {actually - not, ahaha}
As a conclusion: resistance swap rules! : ) {actually - not, ahaha} CapitanVeshdoki
CapitanVeshdoki
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.