openEMS doesn't have a built-in facility for creating Gaussian steps. Most of the analysis I have seen uses frequency-domain techniques, which have their place, but sometimes a time-domain analysis approach is warranted. So, I wrote some code to approximate a Gaussian step function using the built-in facilities of openEMS.
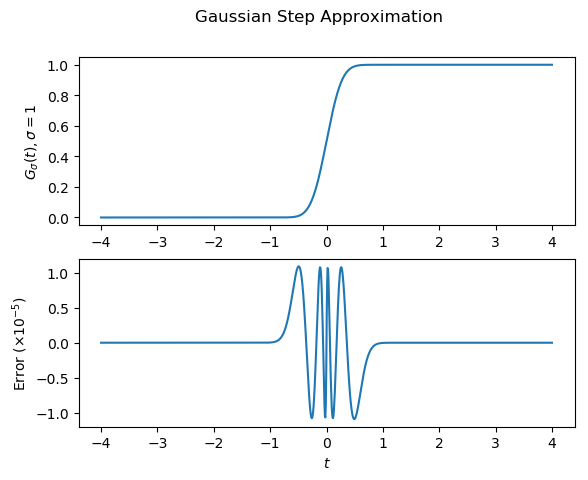
Note that I haven't added this to the openEMS code; it just uses the existing functions. I don't feel comfortable modifying GPL-licensed code. Unfortunately, it took some doing to approximate this function using just those facilities already available in openEMS. But it's done and now available for others to use.
I've documented the derivation of this function in a short PDF document, mostly because it will be easier to find than the dozen or so pages of notes and rambling calculations it took to get here. If you're at all interested, that note gives much more detail than this build log.
openEMS provides a SetCustomExcite() function to allow the user to pass a string representing an excitation function to the FDTD engine, and you can use this to generate a Gaussian step excitation. I'll be posting a log soon to show how it can be used, and why you would choose it over the built-in unit step excitation SetStepExcite().
Here's the octave function to create the step approximation, and return the required Nyquist sampling frequency. Yeah, it's a mess because it has to generate a string representation of the function.
function [string, f_nyquist] = GaussianStep(rise_time, center_time, dB_cutoff)
C = center_time;
sigma = rise_time / (2*erfinv(0.8));
K = 1/sigma;
f_nyquist = 2*sqrt(dB_cutoff/20 * log(10) / (pi*pi*sigma*sigma));
%
% Gaussian step using erf() approximation 7.1.25 from Abramowitz and Stegun
% http://people.math.sfu.ca/~cbm/aands/page_299.htm
%
string = ['0.5+0.5*(', num2str(K), '*(t-', num2str(C), ')>=0)*(1 - exp(-', num2str(K), ...
'*(t-', num2str(C), ')*', num2str(K), '*(t-', num2str(C), '))*(0.3480242/(1+0.47047*', ...
num2str(K), '*(t-', num2str(C), ')) - 0.0958798/((1+0.47047*', num2str(K), '*(t-', ...
num2str(C), '))*(1+0.47047*', num2str(K), '*(t-', num2str(C), ...
'))) + 0.7478556/((1+0.47047*', num2str(K), '*(t-', num2str(C), '))*(1+0.47047*', ...
num2str(K), '*(t-', num2str(C), '))*(1+0.47047*', num2str(K), '*(t-', num2str(C), ...
')))))-0.5*(', num2str(K), '*(t-', num2str(C), ')<0)*(1 - exp(-', num2str(K), '*(t-', ...
num2str(C), ')*', num2str(K), '*(t-', num2str(C), '))*(0.3480242/(1-0.47047*', ...
num2str(K), '*(t-', num2str(C), ')) - 0.0958798/((1-0.47047*', num2str(K), '*(t-', ...
num2str(C), '))*(1-0.47047*', num2str(K), '*(t-', num2str(C), ...
'))) + 0.7478556/((1-0.47047*', num2str(K), '*(t-', num2str(C), '))*(1-0.47047*', ...
num2str(K), '*(t-', num2str(C), '))*(1-0.47047*', num2str(K), '*(t-', num2str(C), ')))))'];
end
 Ted Yapo
Ted Yapo
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.