In this first log i'm going to explain how the kinematic model works.
First thing to take into account is the robot geometry and its DOFs, to ilustrate this, in the next image you see where are they and how they transform. This model is very looking forward, in real robotics first is to make a robust state stimator so you can have smooth meassurements of robots states.
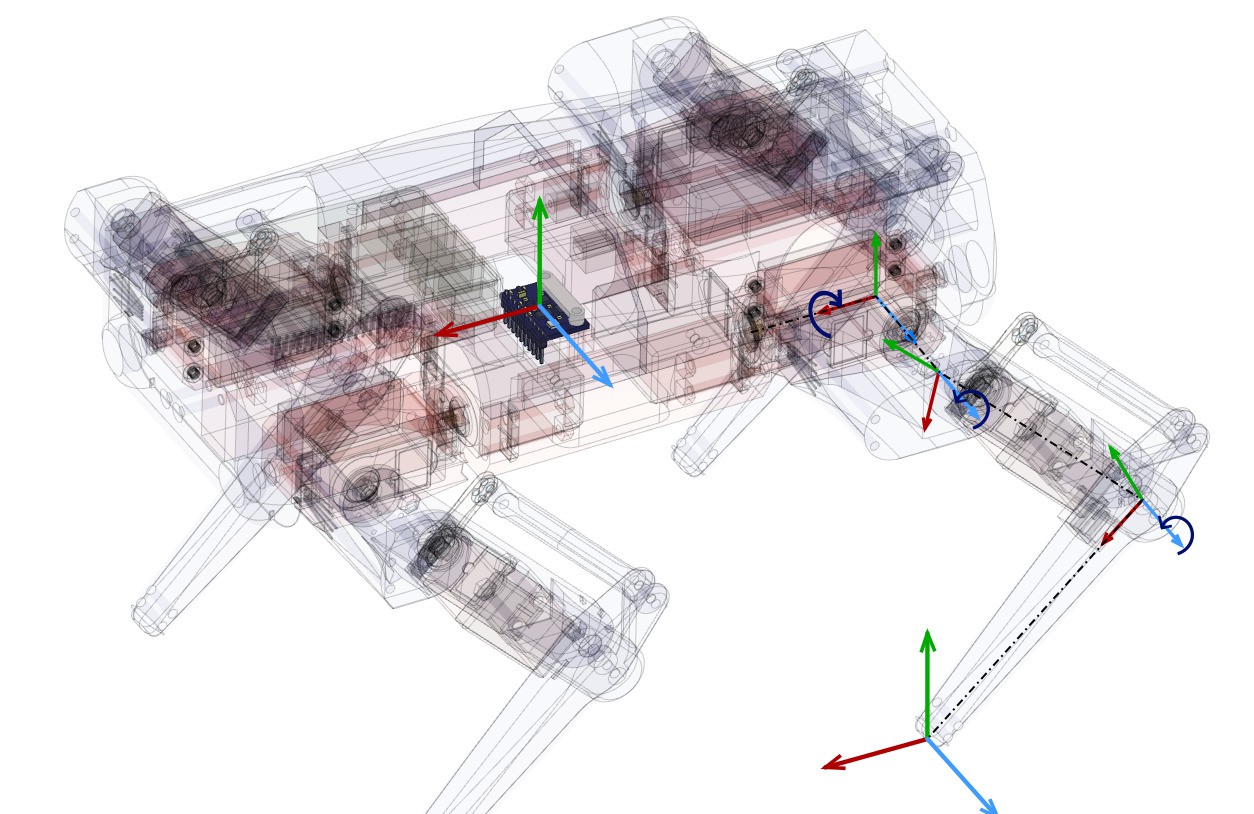
NOTE: All vector are defined inside the robot frame, no world frame is used for now.
So, we have 4 frames on each leg and one which is commun for all, which is the geometric center of the robot (very close to the CoM).
For our setup, there are 2 important frames on the leg, which are the frame0 (coxa frame or first frame on the leg) and frame4 (foot frame or last frame on the leg).
So now, we are going to calculate Inverse Kinematics between those frames. If you want more information on how to calculate IK you can read this article: https://www.researchgate.net/publication/320307716_Inverse_Kinematic_Analysis_Of_A_Quadruped_Robot
As u can see the setup is a bit diferent, but it only change the simetry of the legs, so the analytic function is the same.
Inverse Kinematics are solved on the IK_solver.py file, which is basically two functions, one for right legs and the other for the left legs. These functions works as shown:
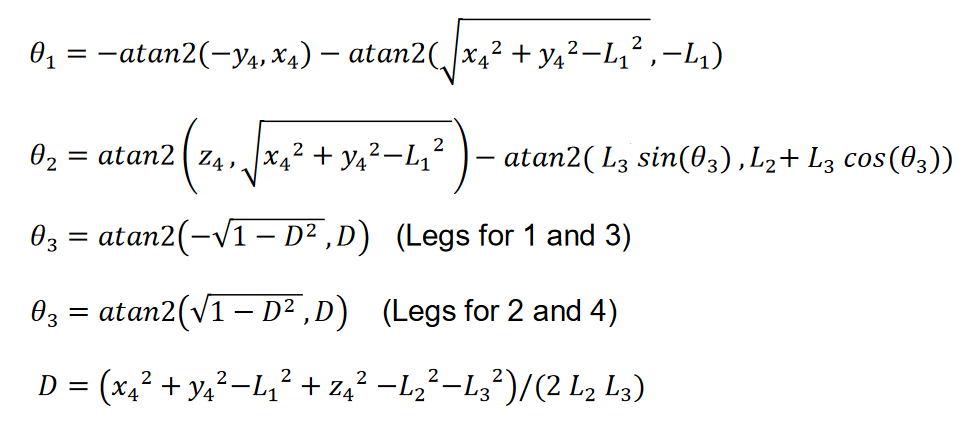
And the code goes as follow:
def solve_R(coord , coxa , femur , tibia):
"""where:
coord = np.array([x4,y4,z4])
coxa = L1
femur = L2
tibia = L3
"""
D = (coord[1]**2+(-coord[2])**2-coxa**2+(-coord[0])**2-femur**2-tibia**2)/(2*tibia*femur)
D = checkdomain(D) #This is just to deal with NaN solutions
gamma = numpy.arctan2(-numpy.sqrt(1-D**2),D)
tetta = -numpy.arctan2(coord[2],coord[1])-numpy.arctan2(numpy.sqrt(coord[1]**2+(-coord[2])**2-coxa**2),-coxa)
alpha = numpy.arctan2(-coord[0],numpy.sqrt(coord[1]**2+(-coord[2])**2-coxa**2))-numpy.arctan2(tibia*numpy.sin(gamma),femur+tibia*numpy.cos(gamma))
angles = numpy.array([-tetta, alpha, gamma])
return angles
Now, we can locate foot in the 3D space, inside the frame0.
Next step is to move the body frame in relation with the feet. Which is essentialy the kinematic model i built, kinematic_model.py file in the code.
For this, we need to define 3 vectors, the vector from the center to the frame0 or coxa frame is going to be rotated and translated with the desired body position.
The next is the vector from body frame to frame4 or foot frame, this vector is where we want the foot to stay with recpect to world coordinates.
With this two vector we can calculate the IK vector needed for the inverse kinematics just by subtracting body to frame4 and body to frame0.
Now, we want the body to rotate on its 3 dofs and its 3 logitudinal movements, for this, we just multiply the body to frame0 vector by the rototranslation matrix, shown at the next step:
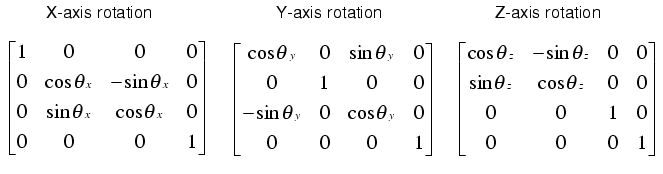
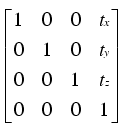
You can see how this woks on the geometrics.py file, where the fuctions for the rototranslations are defined. You only need to multiply these matrix by the vector you want to transform:
def RTmatrix(orientation, position):
"""compose translation and rotation"""
roll = orientation[0]
pitch = orientation[1]
yaw = orientation[2]
x0 = position[0]
y0 = position[1]
z0 = position[2]
translation = np.matrix([[1, 0, 0, x0],#Translation matrix
[0, 1, 0, y0],
[0, 0, 1, z0],
[0, 0, 0, 1]])
rotation = Rxyz(roll, pitch, yaw)#rotation matrix
return rotation*translation
def transform(coord,rotation,translation):
"""transforms a vector to a desire rotation and translation"""
vector = np.array([[coord[0]],
[coord[1]],
[coord[2]],
[ 1]])
tranformVector = RTmatrix(rotation,translation)*vector
return np.array([tranformVector[0,0], tranformVector[1,0], tranformVector[2,0]])
Here there is a figure to ilustrate the rotation of the body with respect to the feet in the pitch rotation:
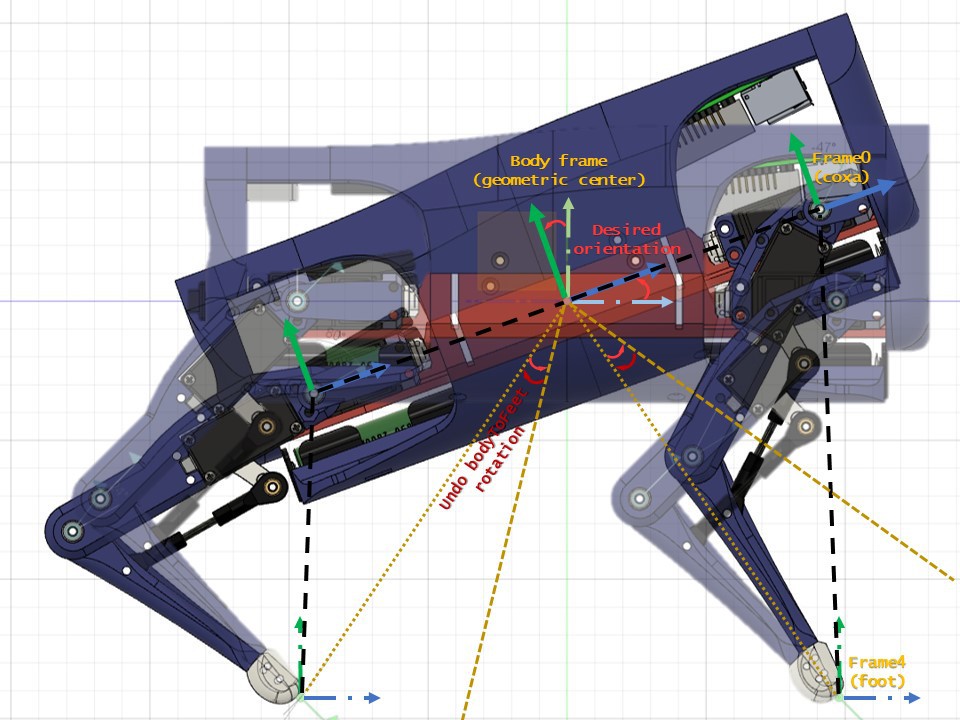
As the the principal frame is transformed, all other child frames are also transformed, so in order to keep feet still, we need to undo the fransformation for the frame0 to frame4 vector (IK vector) before IK are solved. This ends with all frames transformed in order to mantein the the frame4 at the same position with respect the BodyFrame.
Here is the code solving that:
def solve(self, orn , pos , bodytoFeet):
bodytoFR4 = np.asarray([bodytoFeet[0,0],bodytoFeet[0,1],bodytoFeet[0,2]])
bodytoFL4 = np.asarray([bodytoFeet[1,0],bodytoFeet[1,1],bodytoFeet[1,2]])
bodytoBR4 = np.asarray([bodytoFeet[2,0],bodytoFeet[2,1],bodytoFeet[2,2]])
bodytoBL4 = np.asarray([bodytoFeet[3,0],bodytoFeet[3,1],bodytoFeet[3,2]])
"""defines 4 vertices which rotates with the body"""
_bodytoFR0 = geo.transform(self.bodytoFR0 , orn, pos)
_bodytoFL0 = geo.transform(self.bodytoFL0 , orn, pos)
_bodytoBR0 = geo.transform(self.bodytoBR0 , orn, pos)
_bodytoBL0 = geo.transform(self.bodytoBL0 , orn, pos)
"""defines coxa_frame to foot_frame leg vector neccesary for IK"""
FRcoord = bodytoFR4 - _bodytoFR0
FLcoord = bodytoFL4 - _bodytoFL0
BRcoord = bodytoBR4 - _bodytoBR0
BLcoord = bodytoBL4 - _bodytoBL0
"""undo transformation of leg vector to keep feet still"""
undoOrn = -orn
undoPos = -pos
_FRcoord = geo.transform(FRcoord , undoOrn, undoPos)
_FLcoord = geo.transform(FLcoord , undoOrn, undoPos)
_BRcoord = geo.transform(BRcoord , undoOrn, undoPos)
_BLcoord = geo.transform(BLcoord , undoOrn, undoPos)
"""solve inverse kinematics with frame0 to frame4 vector"""
FR_angles = IK.solve_R(_FRcoord , self.coxa , self.femur , self.tibia)
FL_angles = IK.solve_L(_FLcoord , self.coxa , self.femur , self.tibia)
BR_angles = IK.solve_R(_BRcoord , self.coxa , self.femur , self.tibia)
BL_angles = IK.solve_L(_BLcoord , self.coxa , self.femur , self.tibia)
_bodytofeetFR = _bodytoFR0 + _FRcoord
_bodytofeetFL = _bodytoFL0 + _FLcoord
_bodytofeetBR = _bodytoBR0 + _BRcoord
_bodytofeetBL = _bodytoBL0 + _BLcoord
_bodytofeet = np.matrix([[_bodytofeetFR[0] , _bodytofeetFR[1] , _bodytofeetFR[2]],
[_bodytofeetFL[0] , _bodytofeetFL[1] , _bodytofeetFL[2]],
[_bodytofeetBR[0] , _bodytofeetBR[1] , _bodytofeetBR[2]],
[_bodytofeetBL[0] , _bodytofeetBL[1] , _bodytofeetBL[2]]])
return FR_angles, FL_angles, BR_angles, BL_angles , _bodytofeet
Here there is a video showing the model in action:
As you see in the video, you can define a initial position for the feet and vary the 6 dof on the body frame, that it may be, for example, the states of a control model.
 Miguel Ayuso Parrilla
Miguel Ayuso Parrilla
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
i saw theta_2 depend on theta_3 so with your equation. It mean when i rotate theta_3 servo and caculate again, theta_2 will change? any problem with those equation?
Are you sure? yes | no
Great material! Thank you!
Are you sure? yes | no
Hey, thanks for the great explanation. I'm in the process of building my own robot and have a few questions about your formula please.
"alpha = numpy.arctan2(-coord[0],numpy.sqrt(coord[1]**2+(-coord[2])**2-coxa**2))-numpy.arctan2(tibia*numpy.sin(gamma),femur+tibia*numpy.cos(gamma))"
-> Why is coord [0] = z and coord [1] = x? The original formula is different from your code. Usually[0] = x, [1] = y, [2] = z or not?
-> Why is "-" in front of the coord[0]
Thank you :)
Are you sure? yes | no
- " coord [0] = z and coord [1] = x " I think it depends on the way you put elements in the array.
- " "-" in front of the coord[0] " it depends on direction with respect to the frame
Are you sure? yes | no