This log refers to gaitPlanner.py
As in the kinematic_model.py you can change the foot position, you can make a time varying system by changing the feet position describing a bezier curve.
So building a parametric bezier curve (11 points for now) you can follow a closed step loop, i drew this curve on this bezier curve generator: https://www.desmos.com/calculator/xlpbe9bgll
This can by written by an equation dependant of the N point and a parameter going from 0 to 1 in order to describe the trajectory. Here i show you the parametrized Bezier curve:
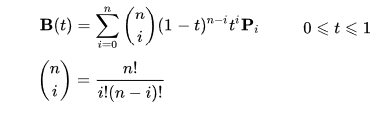
In the the gaitPlanner.py file t is known as phi. This parameter is important, because it tells you where the foot is located, these coordinates are defined inside the foot frame.
The Points are based on the paper Leg Trajectory Planning for Quadruped Robots with High-Speed Trot Gait from the MIT cheetah robot (equations 11-23-24-TABLE II).
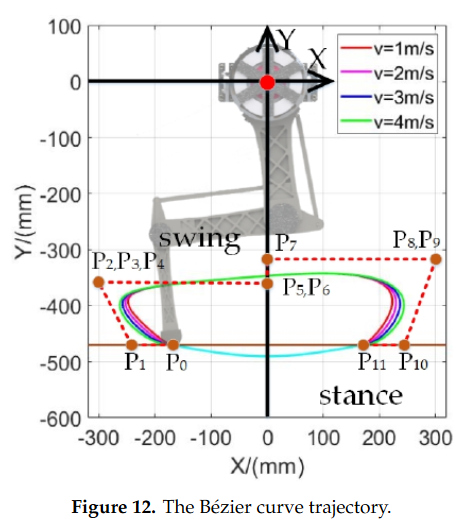
But in my case, i chose similar points but with 10 points (removing P6 and P4) and i'm just multiplying all points by a velocity command in order to make the trajectory wider. This way i have a very simple solution to the stance and swing controller.
Also for every loop, the swing and stance loops are running, each from 0 to 1, first stance phase then swing, with an offset between them which, if it is set at 0.5, both phases last the same. In another case, for creep gait, this offset must be set at 0.75, meaning that stance phase will last 3/4 of the step.
The code for each leg goes as follow, where most of the code is just to define the signs of vectors needed for the rotation steps as this is defines inside cylindrical coordinates.
def stepTrajectory(self , phi , V , angle , Wrot , centerToFoot): #phi belong [0,1), angles in degrees
if (phi >= 1):
phi = phi - 1.
"""
step describes a circuference in order to rotate,
makes the step plane to be inside a circunference.
"""
r = np.sqrt(centerToFoot[0]**2 + centerToFoot[1]**2) #radius of the ciscunscribed circle
footAngle = np.arctan2(centerToFoot[1],centerToFoot[0])
if Wrot >= 0.:#As it is defined inside cylindrical coordinates, when Wrot < 0, this is the same as rotate it 180ª
circleTrayectory = 90. - np.rad2deg(footAngle - self.alpha)
else:
circleTrayectory = 270. - np.rad2deg(footAngle - self.alpha)
"""
then calculate the coordinates to follow the step trajectory
for both ongitudinal and rotational steps.
Here is where the offset between STANCE and SWING is defined.
"""
stepOffset = 0.5
if phi <= stepOffset: #stance phase
phiStance = phi/stepOffset
stepX_long , stepY_long , stepZ_long = self.calculateStance(phiStance , V , angle)#longitudinal step
stepX_rot , stepY_rot , stepZ_rot = self.calculateStance(phiStance , Wrot , circleTrayectory)#rotational step
else: #swing phase
phiSwing = (phi-stepOffset)/(1-stepOffset)
stepX_long , stepY_long , stepZ_long = self.calculateBezier_swing(phiSwing , V , angle)#longitudinal step
stepX_rot , stepY_rot , stepZ_rot = self.calculateBezier_swing(phiSwing , Wrot , circleTrayectory)#rotational step
"""
define the sign of every cuadrant, angle at which the foot is located,
which is saved in order to know the last position of the rotational step.
"""
if (centerToFoot[1] > 0):
if (stepX_rot < 0):
self.alpha = -np.arctan2(np.sqrt(stepX_rot**2 + stepY_rot**2) , r)
else:
self.alpha = np.arctan2(np.sqrt(stepX_rot**2 + stepY_rot**2) , r)
else:
if (stepX_rot < 0):
self.alpha = np.arctan2(np.sqrt(stepX_rot**2 + stepY_rot**2) , r)
else:
self.alpha = -np.arctan2(np.sqrt(stepX_rot**2 + stepY_rot**2) , r)
coord = np.empty(3)
coord[0] = stepX_long + stepX_rot
coord[1] = stepY_long + stepY_rot
coord[2] = stepZ_long + stepZ_rot
return coord
Then making 4 loops going from 0 to 1, for every leg and define an offset for every foot you can do different gaits, here is the code:
if (self.phi >= 0.99):
self.lastTime= time.time()
self.phi = (time.time()-self.lastTime)/T
"""
now it calculates step trajectory for every foot
each step_coord is defined inside the feet frame.
"""
step_coord = self.stepTrajectory(self.phi + offset[0] , V , angle , Wrot , np.squeeze(np.asarray(bodytoFeet_[0,:]))) #FR
self.bodytoFeet[0,0] = bodytoFeet_[0,0] + step_coord[0]
self.bodytoFeet[0,1] = bodytoFeet_[0,1] + step_coord[1]
self.bodytoFeet[0,2] = bodytoFeet_[0,2] + step_coord[2]
step_coord = self.stepTrajectory(self.phi + offset[1] , V , angle , Wrot , np.squeeze(np.asarray(bodytoFeet_[1,:])))#FL
self.bodytoFeet[1,0] = bodytoFeet_[1,0] + step_coord[0]
self.bodytoFeet[1,1] = bodytoFeet_[1,1] + step_coord[1]
self.bodytoFeet[1,2] = bodytoFeet_[1,2] + step_coord[2]
step_coord = self.stepTrajectory(self.phi + offset[2] , V , angle , Wrot , np.squeeze(np.asarray(bodytoFeet_[2,:])))#BR
self.bodytoFeet[2,0] = bodytoFeet_[2,0] + step_coord[0]
self.bodytoFeet[2,1] = bodytoFeet_[2,1] + step_coord[1]
self.bodytoFeet[2,2] = bodytoFeet_[2,2] + step_coord[2]
step_coord = self.stepTrajectory(self.phi + offset[3] , V , angle , Wrot , np.squeeze(np.asarray(bodytoFeet_[3,:])))#BL
self.bodytoFeet[3,0] = bodytoFeet_[3,0] + step_coord[0]
self.bodytoFeet[3,1] = bodytoFeet_[3,1] + step_coord[1]
self.bodytoFeet[3,2] = bodytoFeet_[3,2] + step_coord[2]
return self.bodytoFeetIn order to ilustrate this, here is a diagram which shows the stance face in gray along phi for each foot.
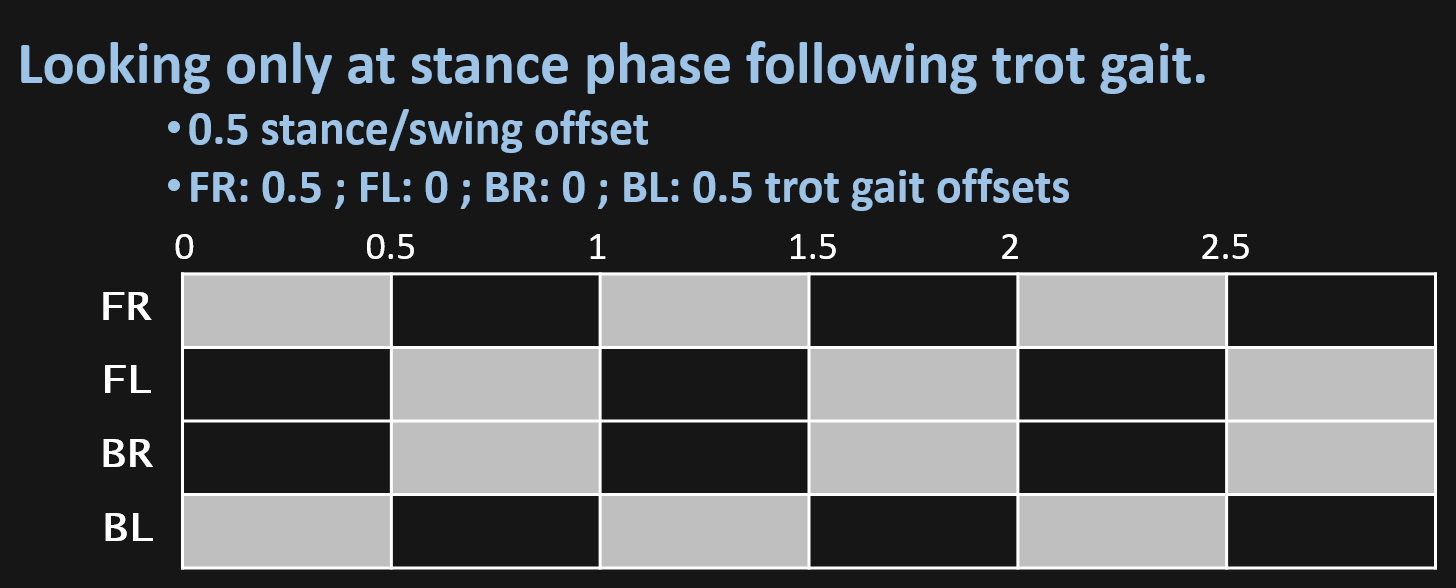
In the video i explain how you can generate different gaits just by changing the offset between the feet loop:
You can play with the simulation at the walking_simulation_example.py file just python3 with pybullet and numpy needed to run the simulation.
 Miguel Ayuso Parrilla
Miguel Ayuso Parrilla
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
May I ask why did you adopt Bezier Scheme?
On the paper they said Spline Curve is better. (About Efficiency & Stability)
Is that because of Motor Control?
I'm really love this project. Thanks for opening this project.
Are you sure? yes | no
You are right, im my case i choose Bezier becouse its easier implementation. I think there shouldn't be any problem with motor control if spline is implemented.
Are you sure? yes | no