I'm trying to make more videos to show the maths behind the algorithm. It's not easy but I'm progressing. The script of the video is easy to write but can easily go awry. The trick seems to be to prepare all the support material and then comment on them.
So I've been programming some HTML/JS pages to use later.
It seems that the easiest path to explain PEAC is by first going back to Fibonacci, then Pisano and modify it to get PEAC. Then the link with Fletcher is easy to make.

1) http://ygdes.com/~whygee/PEAC/fibo.html shows the Fibonacci sequence. There is nothing new there, it is very well know already, but I set the stage for the next slides with two things:
- I show the sequence of numbers in a X-Y graph with increasingly sparse points on a diagonal line with a constant slope.
- I show the convergence of the ratio of consecutive numbers toward φ=1.6180339887498948482045868343656381177203091798057628621...
This is a reminder that φ is a transcendental number, like π. In fact, by its definition, it's the "most transcendental" because its continuous fraction is the simplest. Transcendentals are very interesting because they can be the source of (almost) infinite sequences of finite values.
From there, there is hope that a pseudo-random number generator (PRNG) could be derived from the Fibonacci sequence.
2) http://ygdes.com/~whygee/PEAC/pisano.html is a modification of the above page, with the integer values bound in the 0..15 range: this is the Pisano sequence modulo 16. This value was chosen because we computer guys love powers of 2.
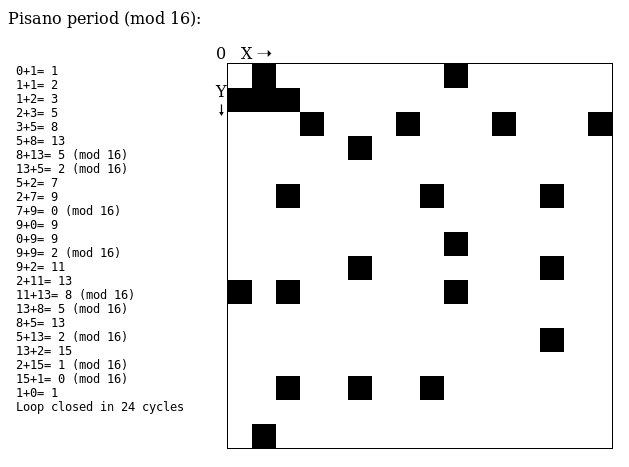
By representing the sequence of values in X-Y form, we see the dots filling only a small proportion of the whole statespace. Here, X is the current value and Y is the last value. Except near the origin, most dots look equally spaced. Larger moduli will not give better fill results because it is well known that for our cases (powers of 2), the sequence loops after 3/2×modulus. Indeed, the program stops after 24 cycles for a modulus of 16. This is far from being a good pseudo-random number generator... Other moduli can be tested but none creates a sequence near modulus squared. See sequence A000045 in the OEIS, and the related Wikipedia page.
But we're almost there !
3) Now let's modify the algorithm a little. http://ygdes.com/~whygee/PEAC/pisanoEAC.html adds a little twist:

Every time the sum wraps around, the next computation adds 1 to the sum.
This single trick bumps the sequence length to 135 values, which is a bit more than 16²/2=128.
The sequence fills only half of the state space, the other half is filled by an identical/complementary sequence. Although it is not ideal, it is "more than good enough" for many applications.
The real problem is to use moduli where the state space contains only 2 orbits. For the powers of two, only a few have been proved so far:
2², 2³, 2⁴, 2¹⁰, 2¹⁶. The video below shows some of these "good" sizes, with each color corresponding to an individual sequence, or "orbit":
Other sizes (non-power of 2) are not practical, and sizes beyond 2²⁵ get extremely hard to compute. However the width of 16 bits is very convenient and is the basis for the PEAC checksum algorithm. More sizes are being explored.
When a suitable width is found, it can be used as the basis for a checksum. A "good" checksum is a PRNG that is perturbed by external data. This perturbation has been studied (the addition is the safest method) and the stability has been proved, so PEAC could be an enhanced replacement to the classic Fletcher checksum algorithms, which have a very similar structure and complexity, but worse behaviour in many corner cases.
 Yann Guidon / YGDES
Yann Guidon / YGDES
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.