The apparently simple task of deciding which symbols go where on the math keyboard has been more challenging than I had anticipated.
The main problem is lack of real-estate. Consider that the keyboard only has 16 buttons, while Wikipedia lists hundreds of mathematical Unicode symbols:
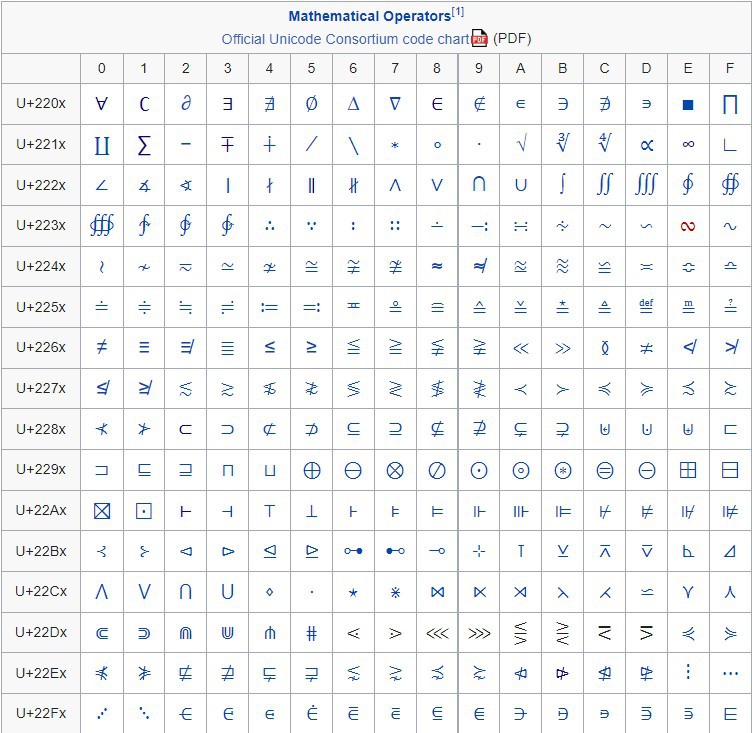
Clearly, it will not be possible to fit every mathematical symbol on the math keyboard. We have two ways of approaching this problem:
- Fit more than one symbol on each button
- Focus on the most-used symbols
The second solution is a bit more tricky because it requires us to make a decision about which symbols common enough to be granted a spot on the math keyboard.
Fitting several symbols per button
This approach is easy. Everyone is already used to the concept of keyboard buttons having more than one symbol. Just look at the number row, for example. They all have numbers and symbols on each button.
For the mathematical keyboard, I decided to fit 6 symbols per button. This may sound like it will get confusing very quickly, but I think it'll work fine. I take advtantage of the fact that the keycaps have a sloped front so one can see symbols printed on the front face.

The button is separated into two columns of symbols: A blue A-column, and a cyan B-column. f you simply press the button, you get a. If you hold Shift while pressing the button, you get A. If you hold Alt while pressing the button, you get α, the front-facing symbol. The same is true for the cyan B-coloumn, which is accessed by holding down Opt. So, Opt+button gives b. Opt+Shift+button gives B. And Opt+Alt+button gives β.
Therefore, by giving up only 3 buttons for Shift, Alt, and Opt, we can fit 6 times as many symbols on the remaining 13 buttons. And by a lucky coincidence we can exactly fit the 26 greek letters by placing two on each button! Perfect.
We can push this approach even further by allowing certain symbols to have multiple different versions accessible by double-tapping, triple-tapping, or even quadruble-tapping the same button. This is useful for certain symbols like roots (√, ∛, ∜) and integrals (∫, ∬, ∭). It can also be used to negate symbols (∈∉, ∃∄), or to access uppercase-versions of letters (δΔ, θΘ, σΣ).
Selecting the most commonly used symbols
This part has been difficult. The goal of the math keyboard is to be as useful as possible to as many people as possible, which means that the symbols that go on the keyboard must be the most commonly used ones. But what is a "common" symbol? I decided to refer to Wikipedia on this matter, with their excellent Glossary of Mathematical Symbols.
From this article and based on my own experience, I decided on the following groups of symbols (with a few examples in paranthesis):
- Greek letters (α, β, γ)
- Comparisons and equivalence (≠, ≈, ≪)
- Algebra and calculus (∑, ∫, √)
- Set theory (⋂, ∈, ⊂)
- Logic (⇔, ∃, ¬)
- Diacritics and supscripts (◌̂, ◌̃, ◌⁰)
- Various others (⋅, ±, ∞)
These groups should hopefully cover most of what a regular mathematician, phycisist, or engineer will need. It is of course likely that many users will miss a few special symbols that they need often, but this is unavoidable.
The layout
I eventually decided on the following layout:

Each key is separated into a light 2x2 top face and a dark 2x1 front face. Each key also has a green main section and blue Alt section.
The symbols with a red triangle in corner has additional symbols accessible by multi-tapping the key. Double-tapping greek letters gives their uppercase versions if they differ from the Latin alphabet. So double-tapping σ will give you Σ, but double tapping α does nothing since that would just give you an A.
Double tapping the set theory symbols will negate them. For example, double tapping ∈ gives you ∉.
For all other symbols, multitapping will access additional versions of the same symbol. For example, double tapping ≪ gives you ⋘. Double tapping ◌₀ gives ₁, triple tapping gives ₂, and so forth.
 Magne Lauritzen
Magne Lauritzen
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.