First, get the Excel Paper Model of the Enigma Z30 here:
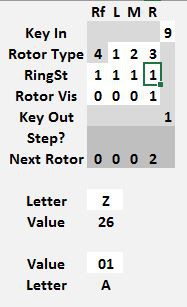
Once the file is opened, find the following section on the left panel of the Enigma tab.
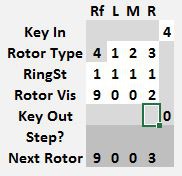
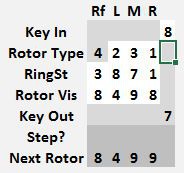
This is the control panel where the Enigma Z30 model is operated.
Data can only be entered on the white squares.
On the Key In row, the number to encode can be entered
On the Rotor Types row, the left, middle and right rotors can be set, use the 1, 2 an 3 rotors only once. The reflector is fixed to type 4 and cannot be altered.
Below, on the Ring Setting row, each rotor can have its stepping point and relative position of the contacts altered. When the ring setting is 1, the rotor steps at the 9 -> 0 transition. If the ring setting is 0, the rotor steps at the 8 -> 9 transition, if set to 2, it steps at 0 -> 1. Each rotor, including the reflector can have its own different ring setting.
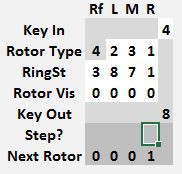
The Rotor Vis row sets each rotor position. Every time a new key is encoded, first the rotors advance to the next position, and then the key is encoded. The next rotor position is shown a few lines below in the Next Rotor row. In the example shown, the rotors were originally set to 4 3 2 0 and when the key 5 was pressed, the machine changed the rotors to 4 3 2 1 and then encoded 5 into a 9.
The encrypted value for the entry key is shown in the Key Out row. In this example, 5 encrypts to 9.
As an aid to encrypting text, two conversion fields are shown at the bottom, one converts letters A..Z to numerical values 01..26 and the other field converts a number in the range 01..26 to a letter A..Z
---
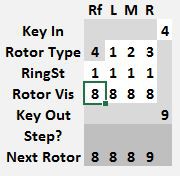
To encode some values with a starting rotor position of 0 0 0 0, set the machine as shown below. The 9 encrypting to 5 is for a starting position of 9 9 9 9, which advances the rotors to 0 0 0 0. Don't use that value. At this point, just set the Rotor Visible position.

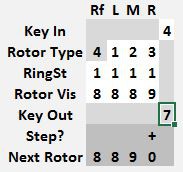
Once a stepping point is reached, the Paper Model will automatically step the appropriate rotor and show the Next Rotor value.

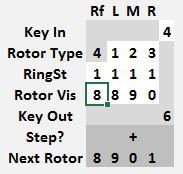
The sequence above shows a starting position of 8 8 8 8 and the number 4 being encrypted 4 times, the output value on the first frame is disregarded, as this frame only sets the starting position of 8 8 8 8 to determine the next position of 8 8 8 9 once the key 4 is pushed. Thus 4444 encrypts to 7600
---
To encrypt text. Type something in the text editor of your choice.
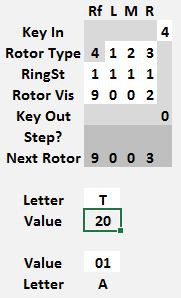
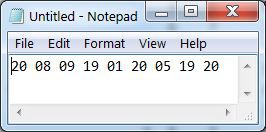
Enter the first letter in the Paper Model to obtain its numeric code of 20.
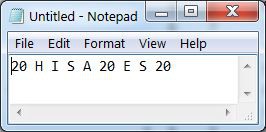
Replace all T with 20
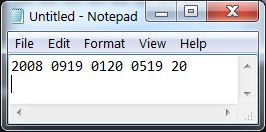
Repeat until all characters have been converted
then arrange in groups of 4 numbers
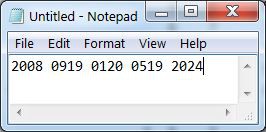
an X (24) can be inserted to pad an incomplete group
then encrypt as usual.
----
To create an actual encrypted message, start by reading the key table for today.
---------------------------------------------------------
|Tag | Walzenlage | Ringstellung | Kenngruppen |
---------------------------------------------------------
| 18 | 2 3 1 | 3 8 7 1 | 537 183 547 654 |The first column is the day of the month. The second column sets the rotor types and order. The next column is the ring setting values. Finally on the last column there are some indicator values to embed in the message to indicate the key used.
To set the machine with this values. Type [AD] 0050 [DA] 02+03+01+03+08+07+01
The paper model can be set as follows:
Then execute the enigma program by typing [AD] 0500 [GO]
Select a random message starting position 8497 and select a random message key 8351.
Set the wheels to 8497 and encrypt 8351
If using the paper model, remember to set the Rotor Visible value, then step the rotors by copying the Next Rotor value to Rotor Vis and entering the Key In value. This yields 7, the first value of the encrypted message key.
The random message key of 8351 encrypts to 7800. Set the Rotor Visible wheels to 7800. The use of a random starting position and random message key ensures messages with the same clear text encrypt to different cyphertexts.
Encrypt the rest of the message
8497 8351 5475 9451 6340 5542 2888 4592Before this sequence of numbers is given to the radio operator to send over the air, you may want to add a header indicating how many groups of 4 characters are in this message and a message sequence number.
To decrypt a received message. Confirm the correct key by matching the first group of numbers in the second row to one of the possible message indicators for the day. Set the machine rotor wheel types and ring settings. Move the rotors to the first group of numbers. Type the second group of numbers to get the message key. Move the rotors to the message key and start decrypting from the second group of numbers in the second row.
Now that you have the theory behind encrypting messages with the Enigma Z30 machine, head over to
http://enigmaworldcodegroup.freeforums.net/thread/102/ewcg-codebook-2017
and give this message a go.
 Arduino Enigma
Arduino Enigma



Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.