In an earlier log we looked at the steady-state conditions to get an idea for how hot the inside of the kiln would get. This helped us get an idea for what thermal conductivity, wall thickness, and heater wattage were acceptable for getting the kiln to the desired temperature. But the steady state analysis does not tell us anything about the rate of heating. It is useful to have an estimate for how long will it take the kiln to warm up and cool down. In this project log we estimate this time-dependent behavior by numerically solving an approximate solution to the transient heat conduction equation.
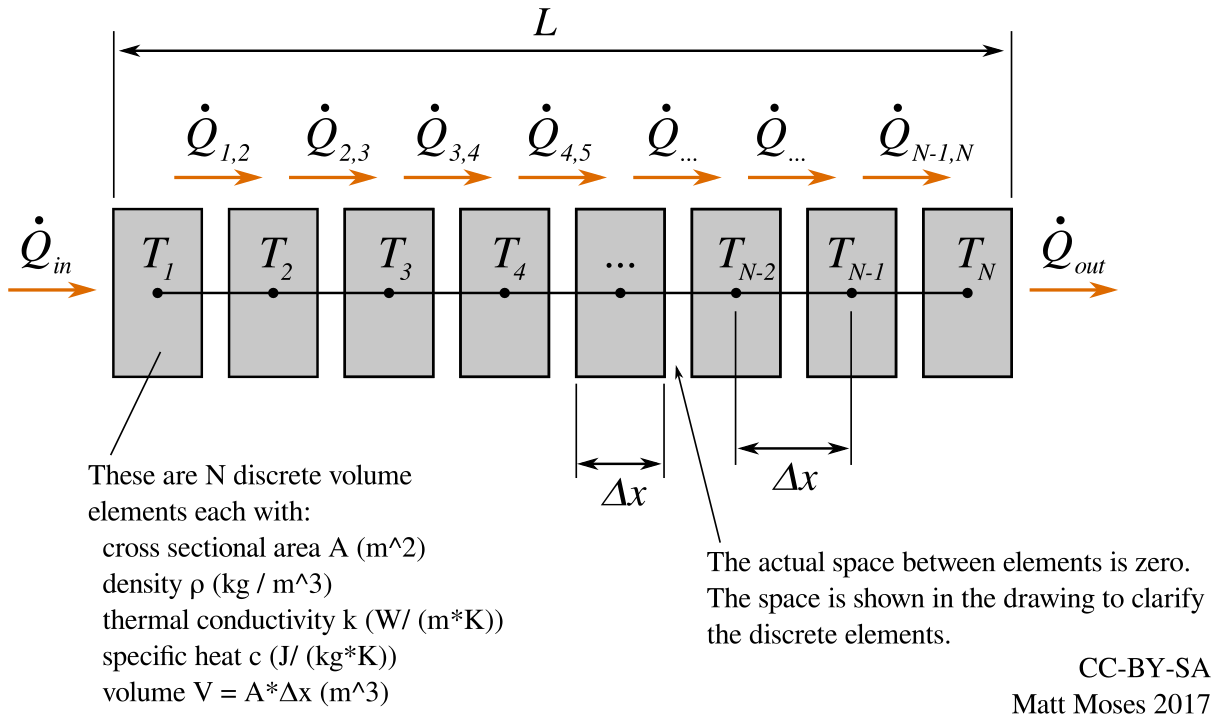
As we did in the steady-state analysis, we use a 1D model - the entire kiln is considered to be just one chunk of "wall". We want to model the temperature of the wall material as we move from inside to outside.
Other assumptions: material properties are constant across x, t, and T. In other words: density, thermal conductivity, specific heat capacity are constant for the entire wall, for all time, for all temperatures.
The partial differential equation that describes heat flow in the wall is
where T is temperature, t is time, k is thermal conductivity, c is specific heat, rho is density, and x is distance through the wall, from inside the kiln to outside. We also need to specify the boundary conditions (heat flow at inside and outside surfaces) and the initial conditions (initial temperature profile of wall) in order to find a solution to this differential equation.
There are many ways to solve this equation analytically. However, we have kind of funny boundary conditions that make an analytical solution somewhat mathematically involved. An alternative way to solve this is to approximate the system as a finite difference equation, and then numerically integrate it using a simple python script.
The first step is to convert the partial differential equation into a recurrence relation with finite differences. The first derivative in time, evaluated at location x, becomes
The second derivative in space, evaluated at time t, becomes
Now we can plug these approximations into the original equation to get the recurrence relation that gives us an approximate solution
The above relation holds for the internal pieces of the wall, but not for the boundaries. At the inside surface of the wall, we need to look at the heat transfer from the heater. At the outside surface, we need to look at the convective and radiative heat transfer to the surroundings.
For the volume element on the inside boundary, where x = 0, we have
For the volume element on the outside boundary, where x = L, we have
where
and
where T_inf is the temperature of the surroundings, sigma is the Stefan-Boltzmann constant, and h is the convective heat transfer coefficient.
Now we have all we need to write a little script to iterate the recurrence relation. You can find a python script that does this called kiln_heatup.py on the RepKiln GitHub repo.
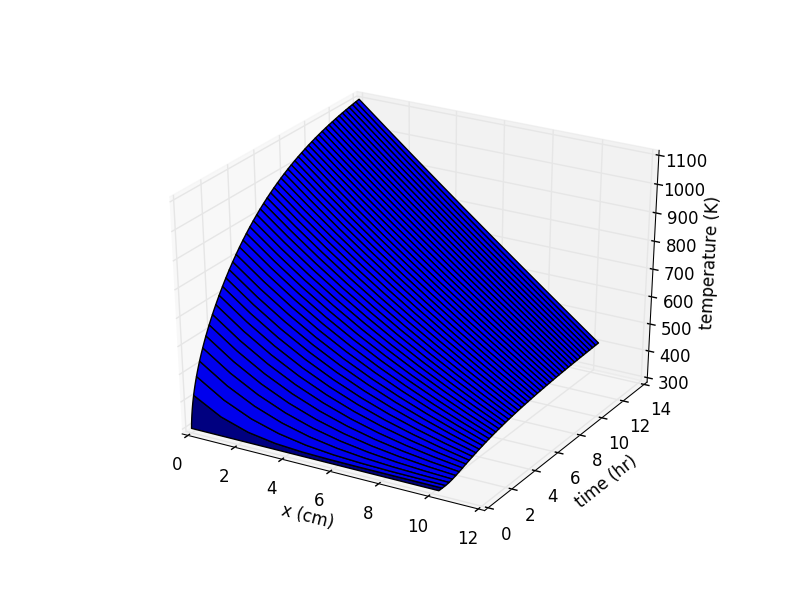
The two plots below show the output of the python script. In the first plot, showing warmup, the initial condition has the wall at a uniform temperature of 300K. Heater power is 1500 W. It takes about 14 hours for the temperature inside to rise to 1100K (830C or 1520F). The x coordinate is distance through the wall from inside (x = 0 cm) to outside (x = 10 cm). A minor note: x actually defines the location of the center of each discrete volume element, so the actual inside and outside wall surfaces are located at -dx/2 and L+dx/2 respectively. But since dx is pretty small, this error is negligible, or at least negligible compared to all the other errors in the model!
We can solve for the temperature during cooldown. We set the initial condition to the wall temperature profile after warmup, set the heater power to 0W, and iterate again.
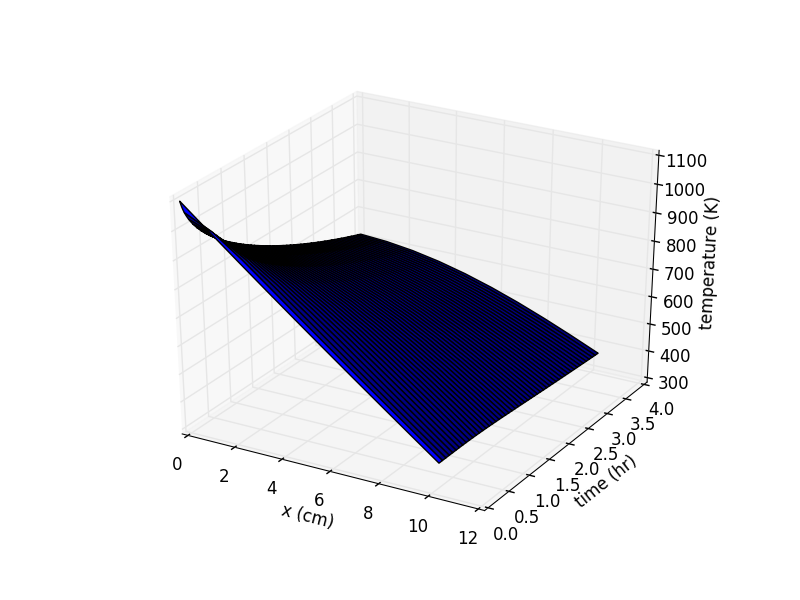
The take home message from this analysis is that the kiln is going to be slow. Fourteen hours is a long time to wait to get up to 1100K. We can hope that perhaps the model is conservative and the kiln will heat up faster. Or perhaps we can look at ways to increase the heater power to get a higher temperature.
 Matt Moses
Matt Moses
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Matt, where do your boundary equations derive from? Is it the same Central difference approximation as you use for the interior points? if so, then where does the factor of two go in front of the T(0,t) term? I have tried to derive them myself, but nothing seems to be connecting.
Are you sure? yes | no