The algorithm presented on the project description is, in fact, a special case where both addends have the same range.
In the colorspace decomposition algorithm however, there are 3 addends, with the same boundaries but the intermediary sum Cgb has twice the range of the R component. Combining R and Cgb creates a new set of problems...
First : one addend's boundary is larger than the other. The algorithm requires a clear ordering to work, so we must swap the operands in a preliminary step, if the order is not respected.
0 ≤ a ≤ m, 0 ≤ b ≤ n, 1) initial setup: S = a + b, l = m + n 2) operand swap: if (m < n) then swap (a, b), swap (m, n) fi
(edit 20170607: removed o and p because they were useless)
Now that it's out of our way, we can focus on what to do with these data and what happens to them.Let's focus on the data table of the Project Details Page.
What this amount to, is: a square of side n, cut in half at the diagonal (that corresponds to S==n). One half of the square has a normal numbering of the columns, the other half has a reverse numbering.
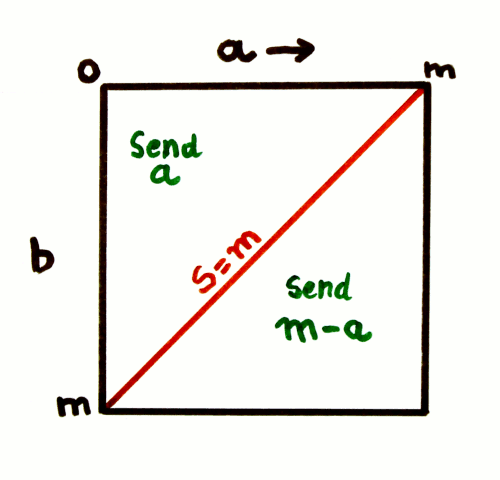
What happens when m > n ?
In a geometric sense, this amounts to cutting the square at the S=m diagonal and moving the lower/reversed part away from the higher part, creating a new zone between them.
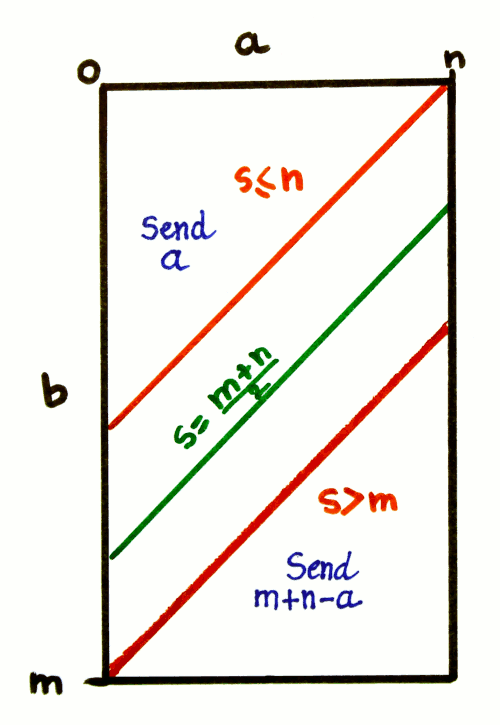
The diagonal of the square is the place where two things happen:
- the operand is reversed: a becomes m-a
- the range of a is also reversed
However when the limits are different, these two things do not happen at the same place anymore.
- The reversal of a must occur at the middle of the rectangle, so there are as many direct codes as there are reversed codes. This does not occur at n or m, but in the middle:
if ( S > l/2) then a = l/2 - a; fi
- The range decreases at S>m, increases at S≤n, but between these bounds, it does not change: there is a saturation region.
if (S < n) then range = S (increase) else if (S > m) then range = l - S (decrease) else range = n (saturate) fi fi
These tests can be run in parallel, but also in series, because the conditions are co-dependent: n < l/2 < m. The code segments can be merged:
3) Reversal:
if (S ≤ l/2) then
range = S
else
range = l - S
a = l/2 - a
fi
4) saturation
if (range > n)
range = n
fiOf course, the decoding is symmetrical, it reuses the same formulas to compute the requested range and adjust a.
Conclusion
This general algorithm works for m=n, and the special case presented in the main page is just an optimisation and simplification. The special case is faster and more compact but the general case is more powerful and potentially more efficient.
In the context of 3R, when m != n, the trivial approach for encoding one of the data is to send the one with the smallest range. The above algorithm goes further:
- it reverses the encoded number, which makes it easier eventual further entropy coding steps
- it reduces the range of the encoded number, when it is known to not exceed an implicit limit.
Taken together, these elements significantly increase the packing density with no pathological case or increase of the original data (to be demonstrated). These improvements would be impossible without the knowledge of the respective limits of the operands.
 Yann Guidon / YGDES
Yann Guidon / YGDES
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.