My supercapacitors arrived yesterday, and I've had a chance to do some tests with them. I set up a test rig where I can log data while charging the caps. I don't have the charge balance boards back from OSH Park yet, so I've been testing a single capacitor.

The test setup includes three serial-port-enabled DMMs and a steel ammo can to contain the coin cell just in case it bursts during high-rate discharge.
Here's an interesting bit of trivia: a CR2477 coin cell is rated to deliver 10,800 J of energy. The 7.62mm NATO rounds originally stored in the ammo can have a muzzle energy of 3,304 J, so the coin cell can deliver as much energy as three .30-caliber rifle bullets. Just much less quickly.
Here are six of the capacitors, 400F each:

I bought eight of them, figuring that a few extra to play around with could be fun :-) I'll probably wire them together in this in-line arrangement, which will place the output terminals close to where they would be on a car battery; this will make it easier to connect the car's battery cables to the capacitor pack. I might print a case for them just for fun.
I arranged a simple test overnight to measure the capacitance and self-discharge rate of a single capacitor. I charged the capacitor for a while, then logged data while it "self" discharged. This discharge was due to a combination of true self-discharge, leakage through the 1N5817 diode, and the over-voltage protection circuit, which is a 10k trimmer and a TL431 shunt regulator. As a fist approach, I've chosen to model all the leakage as a parallel R, treating the whole thing as a single RC circuit.
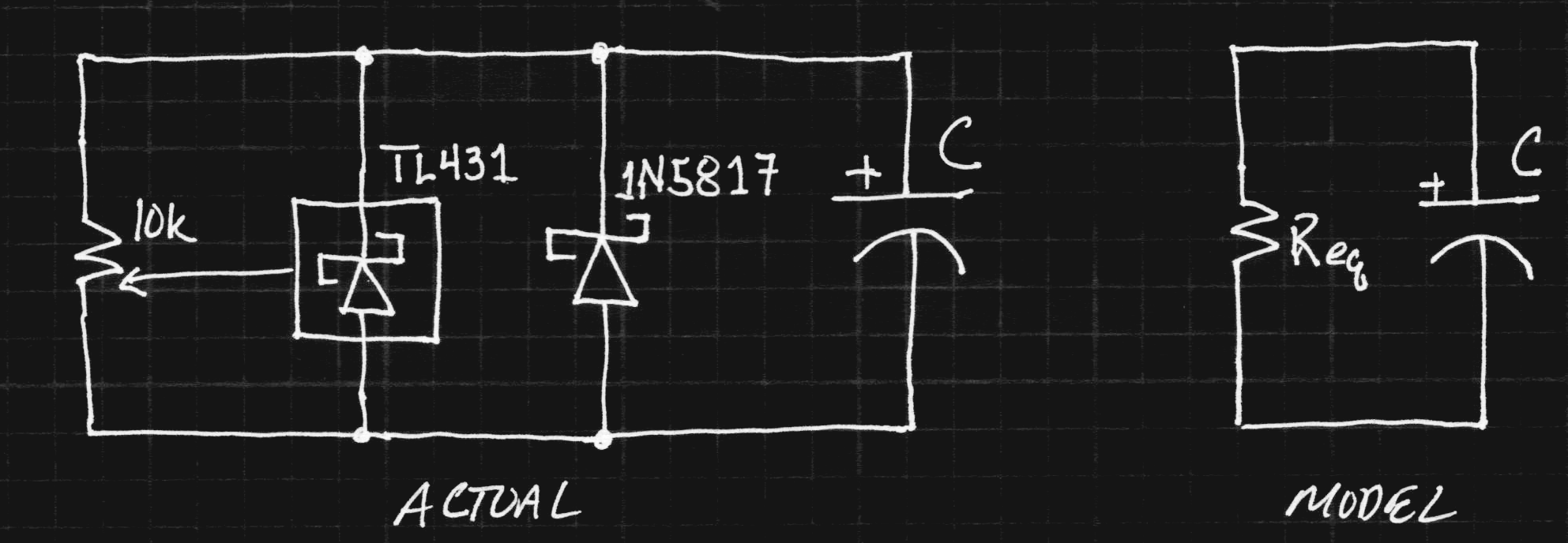
If I knew the actual value of the capacitance, I could determine Req from the discharge curve. So, in order to find both the Req and capacitance value, C, I added an extra 10-ohm resistor across the capacitor and continued to log the voltage. The result is a pair of exponential curves:
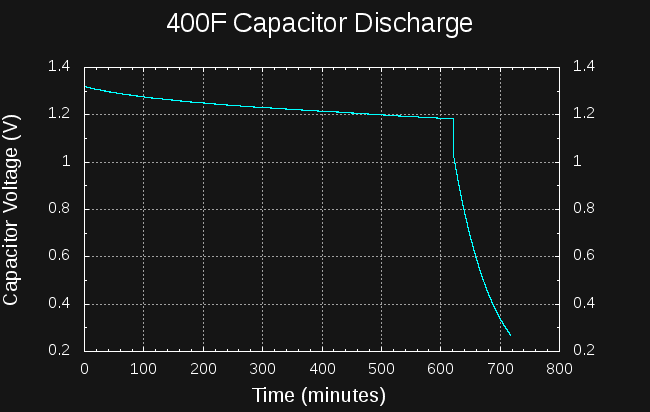
For each curve, I estimated the RC time constant by linear regression; To do this, you can re-arrange the equation:
to get:
which is easily recognized as the form (y = a x + b), so can be fit with linear regression.
For the first part of the curve, this yields an estimate of 330,914 for the RC time constant. For the second part (with the 10-ohm resistor added in parallel), the RC time constant is now much lower, 4298. Combining these two measurements allows us to determine Req and C, since we have two equations for the two unknowns:
Solving these equations simultaneously (I used maxima) yields C = 435F, and R = 760 ohms.
The capacitance seems reasonable for a 400F -10/+30% part, but the equivalent resistance seems low - this would mean a leakage current of 3.5 mA at a fully-charged 2.7V. The capacitor itself has a maximum 1mA leakage, the Schottky diode 1mA (at 20V reverse voltage, so it should be lower here), and the potentiometer and regulator should be only a few tens of uA maximum. Looking at it another way, with RC=4298, the capacitor will lose 10% of its energy in 3.7 hours, or half of its energy in 25 hours.
I will measure the leakage current of the TL431 and Schottky diode separately, and see what those look like.
This isn't necessarily terrible news, though, since I don't intend to leave the capacitors connected across the charger when it isn't running. Now, I need to re-do this experiment without the charger connected to get a better estimate of the self-discharge of the capacitor alone.
EDIT: some of the "extra leakage" I detected is probably due to dielectric absorption issues. I see the datasheet specifies 1mA maximum leakage after 72 hours - I interpret this to mean the capacitor is "soaked" at the maximum voltage for 72 hours to ensure fully saturating all the theoretical little RC's inside before testing leakage. I do notice that there's a quick "step change" in capacitor voltage when first applying a charge or load - probably reflecting a shallow charging or discharging. I can probably avoid most of the self-discharge issues by arranging the engine starting test to happen right at the end of charging.
 Ted Yapo
Ted Yapo
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.