The numbers are in on the self-discharge test. I charged a 400F capacitor to 2.33V with my bench supply, and let it soak at that voltage for about 2 hours. Then, I recorded the capacitor voltage over the next two days while the capacitor self-discharged.
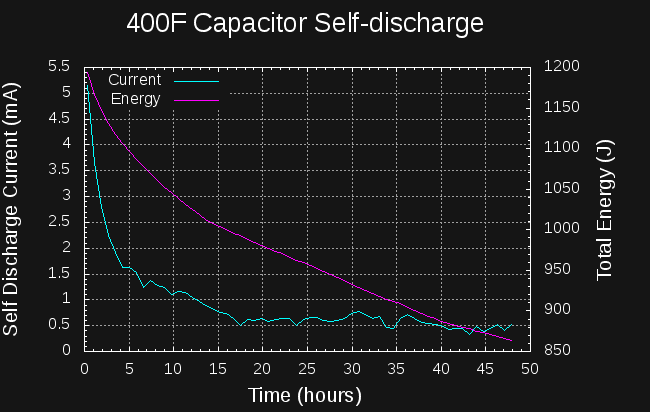
To estimate the self discharge current, I fit a series of lines to the local voltage-vs-time curve using least-squares regression with a window of 2001 points wide (about 45 minutes of elapsed time). Some of the noise in the curve is due to the quantization of the voltage steps.
The datasheet specifies a 1mA maximum self-discharge after 72 hours. The capacitor meets the specification, with the leakage current dropping below 1mA after about 12 hours. After about 16 hours, the self-discharge current levels off at around 0.5 mA. The bad news is that the self-discharge current starts at around 5 mA, so 10% of the capacitor energy is lost in the first 5 hours, extending to 20% lost in 24 hours.
I don't know how this curve would look if the capacitor had been "soaked" for a longer time at 2.33V. It may be that if held at a specific voltage for an extended period of time, the initial self-discharge would decrease.
So far, I'm also not sure exactly how to apply this data to the charging problem. For instance, what does the leakage current look like during charging? Does it increase or decrease as the capacitor charges? In any case, the initial self-discharge current doesn't look good.
 Ted Yapo
Ted Yapo
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.