FM synthesis requires a lot of calculation of sine values, so speed is of the essence.  My worry was that a normal sine function from a math library might concentrate on accuracy over speed and would take an unknown amount of time.  To counter this I made my own, mostly by cheating.  The original fast integer sine function for the Delta Flyer was lookup table based.  An array of 4097 16-bit sine values was calculated with Octave and written to a source file.  Mirroring allowed us to store only a quarter wave with the most significant 2 bits of the angle being the quadrant determining which way to proceed into the table and what sign to give the output.  To deal with the missing 2 bits of entry precision 2 entries were pulled from the table and the bitshift constant multiplication of the last 2 entries used to create a linear interpolation for values between them.  This worked, worked well, and was in line with what I remember of how the Yamaha chips were supposed to work.

I never did actually check if a calculated sine was slower than my LUT method.  I did, however know that the method we used wasn't fast enough to allow a 40khz sampling rate with an arbitrary number of notes simulated with at least an earlier version of the synthesis function.  If the synthesis interrupt routine ran over it would be called again before completion, the DAC would never be updated with the new volume, and the input routines would be starved turning the synthesizer silent and freezing it.  The simple solution with only some days to work with was just to ignore the upper half of the human hearing range and set the sampling rate to 20khz.  This was good enough to allow full sit-on-the-keyboard polyphony and cover the dominant tones of all the notes in our 49-key set anyway.

So, as a thing to do to keep myself technical while concentrating on trying to land my new-grad job I decided to actually benchmark and confirm that assumption.  To do that I needed a calculated sine to test against, unfortunately I wasn't able to get the ARM DSP sine implementation out of my libraries (I'm assuming MBed doesn't keep it to ensure a platform-neutral library), so I just had to make my own.

The gold standard of calculating the sine wave with basic arithmetic is what's called a Taylor series: an infinitely long polynomial in the form of an infinite summation that fits a pattern. 

In the case of sine.  There's a few problems with this, first of which is that it takes literally all of eternity to calculate.  The second is the number format: we want to pass in integers or, thought of a different way, fixed-point values between -1 and 1 while the above polynomial takes in radians, from -pi to pi.  A few scaling constants could fix that, I guess.

A nice helpful thing is that the above infinite polynomial is accurate for a sine wave of infinite length.  With a little bitmasking all we really care about is the first cycle, as said above from -1 to 1.  And our application is audio so the estimate doesn't need to be perfect in shape, just very good.  If we stop the summation at n=4, the x^7 term of the polynomial we get a graph that's the right shape.  The only problem is it crosses the X-axis at 0.98 instead of 1, about 2% early.

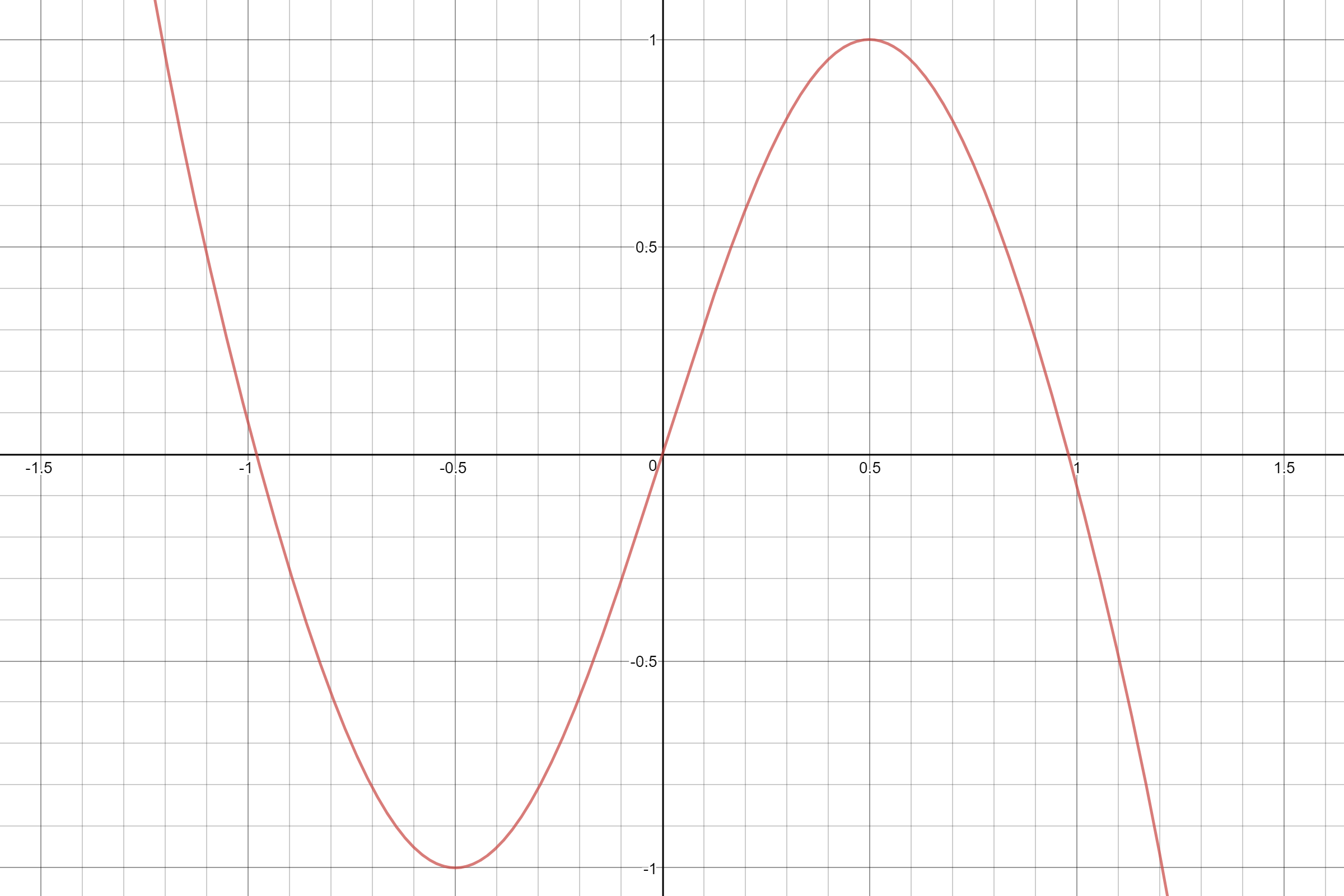
The source of this error is that the Taylor series is only maximally accurate with all it's terms.  if you cut it off early it's not meant to give you an estimate of the same order.  But we know an estimate of this order will work and give us about the right shape.  So let's make our own, besides, multiplying everything by pi is getting old.

We know from the Taylor series, and from the basic fact that our desired graph flips when x goes negative that the polynomial we desire will consist only of odd-order terms.  Now what are the desired features of our curve?

1st. It should reach value 1 at x=1/2.

2nd. That value is the maximum (if not we overflow our number format which is the integer math version of crossing the streams) so the slope or 1st derivative should be zero at x=1/2

3rd. It should be zero at x=1.

4th. (optional but we'll use it for best shape) It should be straight when it crosses the x axis.  So the slope should not be changing, in other words the 2nd derivative / curvature is zero at x=1.

That's 4 facts to work with so we'll build a polynomial with 4 terms.

Let's use basic calculus and take the 1st and second derivative of that.

Kind of looks like a system of equations doesn't it?  Let's put in our facts:

1.

2.

3.

4.

Well whatdoyaknow, we have 4 equations, and 4 unknown constants.  This looks like a job for our frienemy linear algebra.  Let's put all these in a matrix, scaling the fractional ones up just in case and putting the constant term in the right column:

And we'll feed it into an online row reducer because we aren't idiots who end up with errors because we did computation ourselves instead of using a computer.

So our resulting polynomial is:

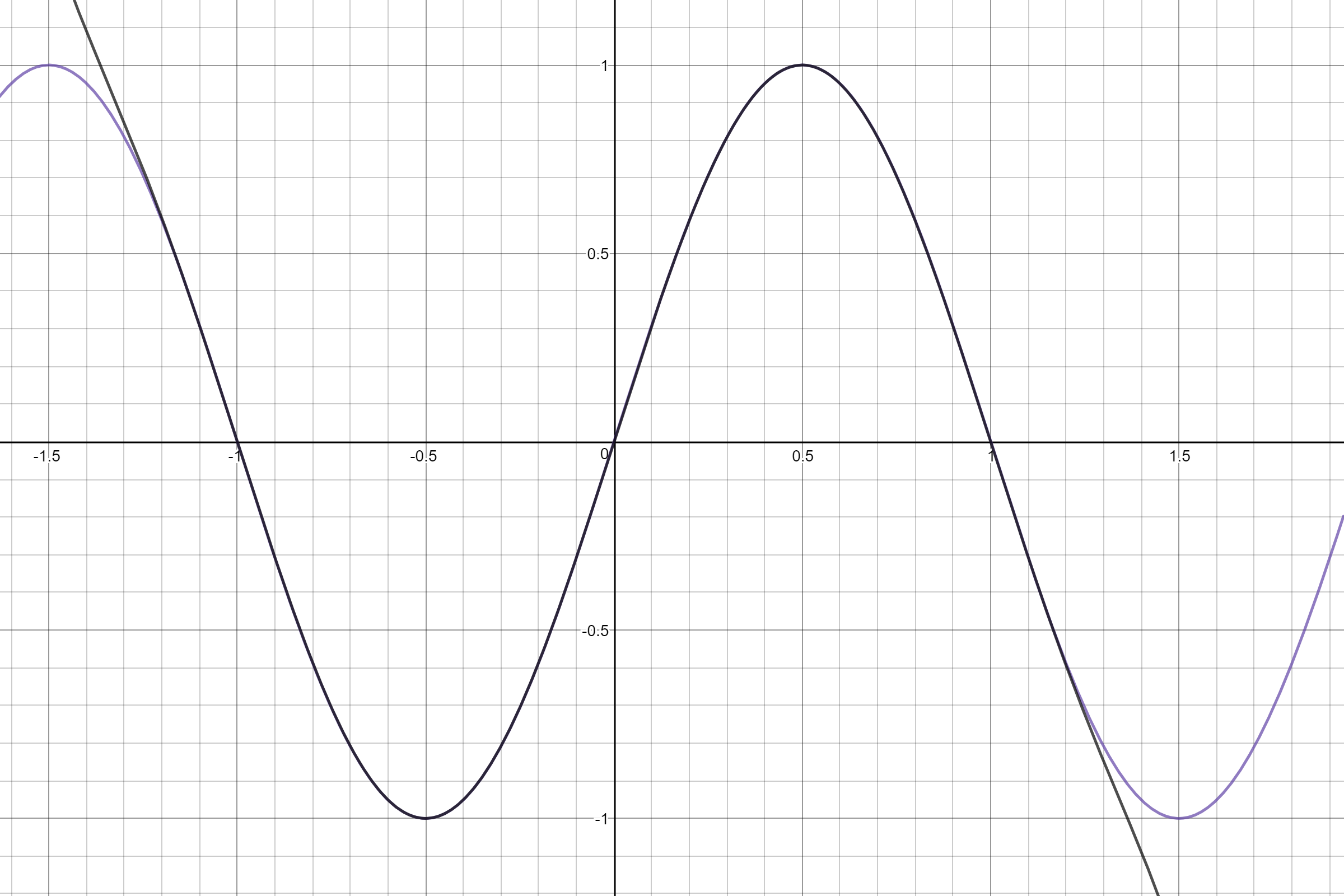
Yeah, that looks like it'll work just fine.  Feel free to steal it, I'm sure it's been calculated before.

To turn this equation into an actual efficient algorithm in C we'll need some optimization as well as conversion into our number format.  The low hanging fruit here is the exponents.  You'll note that

So we can get our powers of x with only 4 multiplications (1 to get x squared, and one each for 3rd, 5th, and 7th powers).  Also we know that division is slow, long-division is a guess and check series of subtractions that can't be added in a tree like multiplication so it's always one of the slowest operations available.  So we won't use it.  We're helped in this by our number format.  Really we want to our answers to be between the upper and lower limits of 16-bit signed integers so all our terms are getting scaled by uint_16t_max of 32767.  We can integrate that into our leading constants and get fractions large enough we can truncate them to integers with minimal error.  We won't do that yet so here's the still-accurate equation:

Similarly we need to scale input to between -2^15 and 2^15 (an actual input of 32768 will get converted to -32768 by the operations we're using to handle input of greater angles anyway so we're safe) instead of -1 to 1.  We'll call that input Q. So

which is a very nice expression of the bitshift we do after every multiplication to re-normalize. For example 

has an extra 2^-15 which isn't part of our number format representing that we need to shift right 15 bits when we store our x-squared value for calculation.  This is about to become important because it solves a problem we've been ignoring: those fraction constants we've been avoiding turning into integers? many of them are greater than 1 in our number format.  This may seem like it's not a problem but if we feed in an angle near 1 the resulting value will overflow the 32 bits we've allowed for the result in our number format.  Sure if we were working in assembly we could pull it from the high register after multiplication but C languages don't actually give us a syntactic way to do that.  Instead we'll borrow a few 2^-1 until the constant is less than 1 and just renormalize by that many bits less after the multiplication.  And here's our algorithm, I may need to tweak the rounding direction of our constants but for right now the results don't overflow the range and are accurate to within about 2/32767 which is well below the noise floor for our application.

int calcsin(const int phase){
    int x = (phase << 16) >> 16;//this truncates our input to 16 bits signed and sign-extends it
    int x2 = (x * x) >> 15;
    
    //beware!!! here there be magic constants
    int sum = (51385 * x) >> 14;

    int xblock = (x * x2) >> 15;
    sum -= (41914 * xblock) >> 13;
    
    xblock = (xblock * x2) >> 15;
    sum += (39072 * xblock) >> 14;
    
    xblock = (xblock * x2) >> 15;
    return sum - ((13261 * xblock) >> 15);
}

So now onto the actual benchmarking:  I built a program that calculated samples for a sine wave (I think it was middle c at 20khz or something), as many as possible in a second.  First using the LUT method with the table as a static constant (so in theory the compiler put it in flash), second with the table as just a non-constant global (to be put in code-segment RAM), and third with the above algorithm.

Here's the results:                                                 

5198338 sines calculated using constant custom interpolated LUT method in 1 second.                                                                   
The last value was ffffabc9
5939341 sines calculated using non-constant custom interpolated LUT method in 1 second.
The last value was 6c3f
6195348 sines calculated using custom fixed-point polynomial in 1 second.
The last value was 5a76
Checking compass points of fixed-point polynomial.
Sine at zero is 0.
Sine at 1/2 is 32767.
Sine at -1/2 is -32765.
Sine at nearly 1 is 2.
Sine at -1 is 1.
Sine at 2 is 0.

Of note is that, on the target board calculating the sine is a little faster, but only just barely.  With a slightly better coded function I might get it to optimize further, or use hand-tuned assembly to really make it work, but it's already faster.  However, this is on an STM32F446 running at 190mhz with a real multiply and even MAC.  There's a very good chance on any slower chip a LUT method would still be faster, even if it's the best option here.