As @Martian created his new architecture #Homebrew 16-bit CPU and Computer, he credited this PDP project for ideas and guidance. In return I take the opportunity to comment on his ALU, which contains typical "misunderstandngs" that I have seen in many other "amateur" designs. These are harmless in a SW simulation but their hardware implementation would be significantly slower, larger and less efficient than what can be done. So this is not at all a criticism of Martian but a little lesson in logic design which, by the way, explains HOW and WHY my own CPU are organised in their precise ways.
Note : ALU design is already well covered there : http://6502.org/users/dieter/ This is a MUST READ but it might focus on particular technologies and here I'll cover some required basics.
At least, Martian's ALU is very easy to understand : there is a big MUX that selects between many results of computations. One input for every opcode. It's large, the many inputs imply a very large fan-in and there is quite a lot of redundancy. See https://hackaday.io/project/131983/log/143820/ :
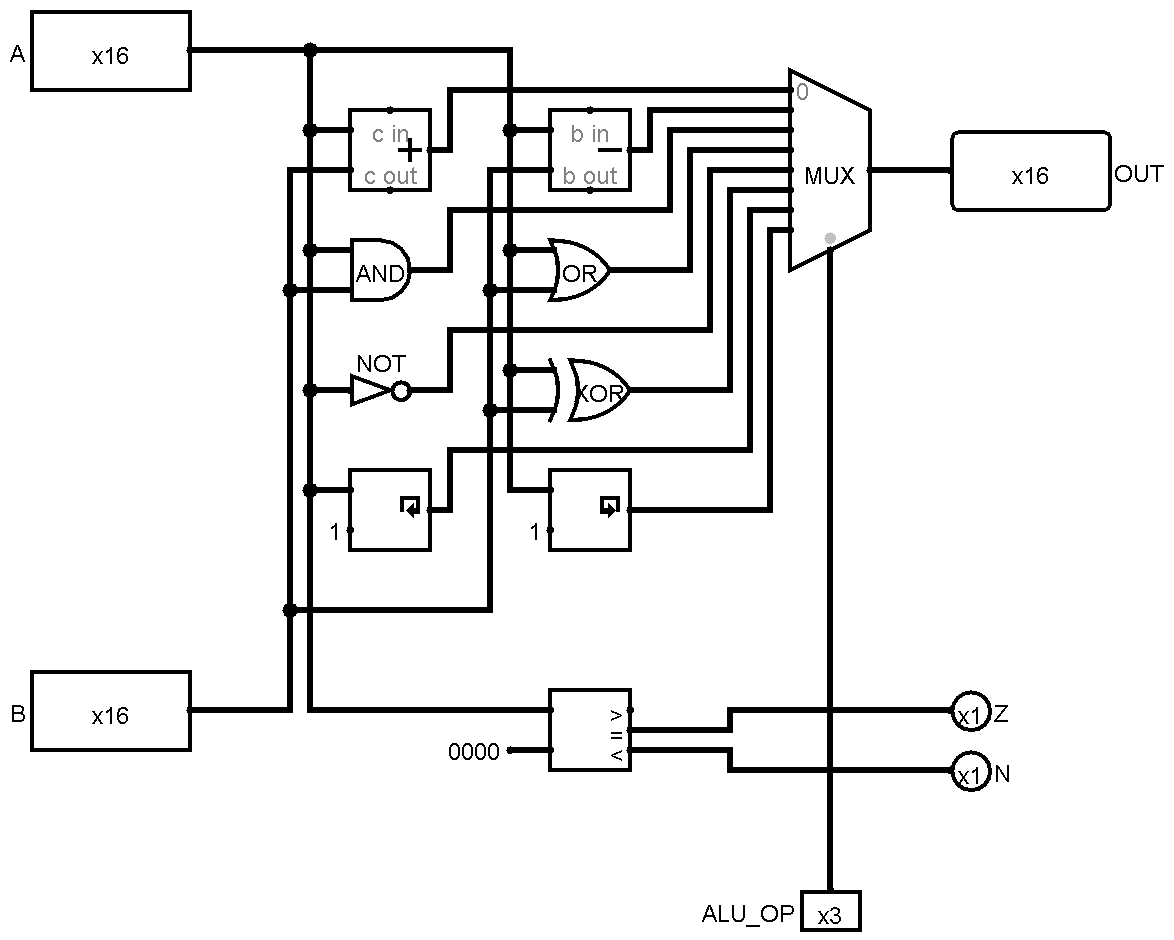
Another version:
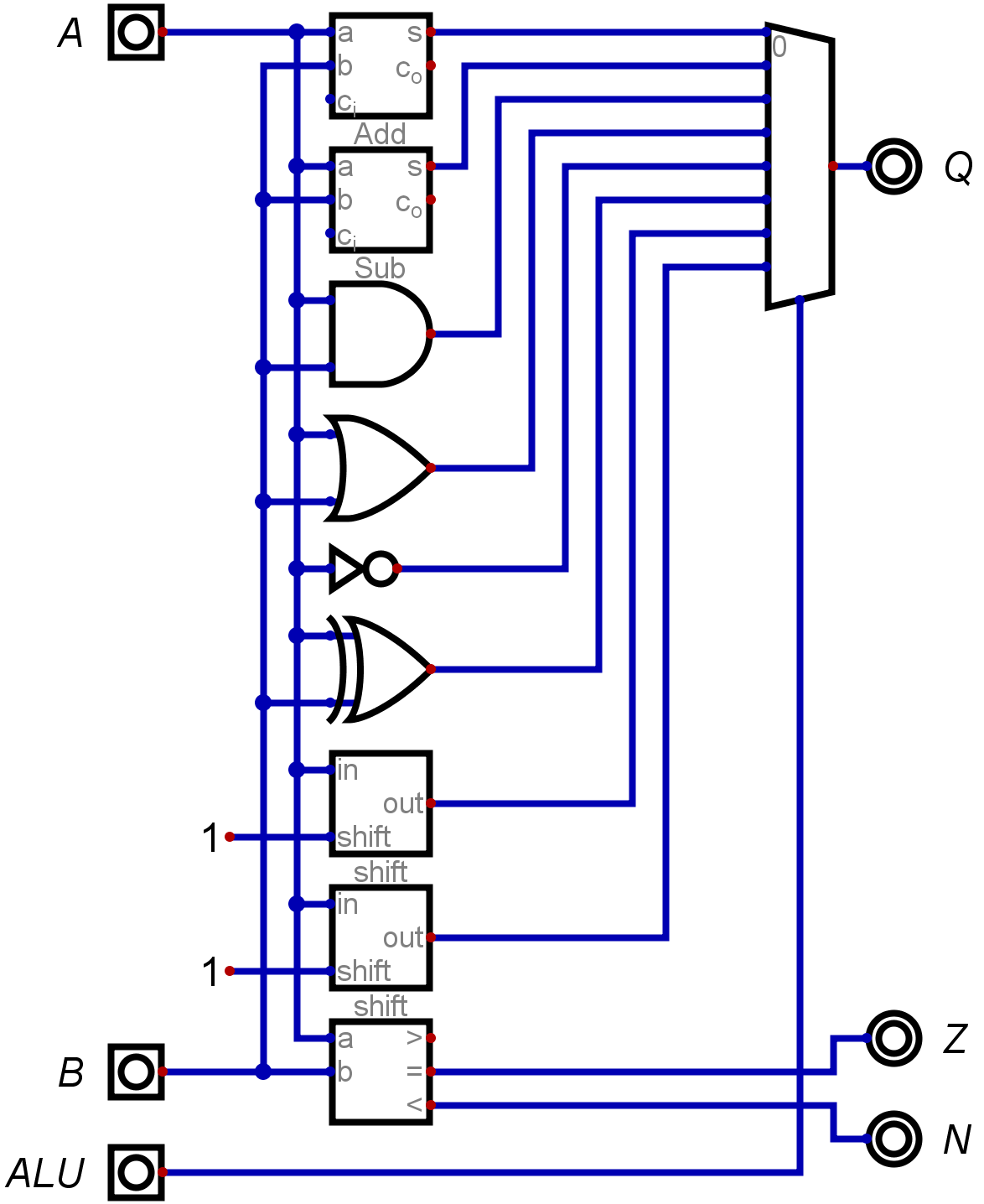
So the name of this game is to factor operations.
I'll simply start with the elephant in the room : addition and subtraction.
In typical code (think C/Verilog/VHDL), you would write something like :
if opcode=ADD then result=ADD else result=SUB
if opcode=ADD
then result=ADD
else result=SUB
Which synthesises into one ADD block, one SUB block and a MUX2. This would be OK if the opcode signal came late but in this case, the opcode is the first thing that we know in the pipeline. The cost is pretty high, because ADD and SUB are actually very very similar circuits so only one is actually required.
The key is to remember that in 2s-complement :
C = A - B = A + (-B) = A + (~B) + 1
C = A - B = A + (-B) = A + (~B) + 1
so if you want to compute C, you need to
- invert all the bits of C (a row of XOR does the trick)
- increment the result
Oh wait, that's another addition unit added to our critical datapath... But sweat not. Since it's only 1, there is another trick : set the CARRY IN bit.
Tadah, you have it : a unit that contains only one carry chain and has the same critical datapath as a MUX-based ADD/SUB, but with
- almost half the parts count / surface / power requirement / etc.
- half the fan-in (because only one ADD is fed)
- a bit more speed
And this is just the first of many tricks in the book...
Another unit in the diagram is a "comparison" block. Which is... well, usually, a subtractor. The carry-out and/or the sign bit of the result will indicate the relative magnitude. But we already have a subtractor, right ? Just execute a SUB instruction and don't write the result back. That's it.
OK so now there is this row of XORs in the critical datapath. Is it a curse or a blessing ?
Actually it is welcome because it helps to factor other operations than the ADD/SUB. In particular, some boolean operations require one operand to be inverted : ANDN, XORN, ORN
So you only need to implement OR XOR and AND and you save even more units (and you reduce the fanout).
But wait, it doesn't stop there ! There is even more factoring to do if you are brave enough to implement your own adding circuit. And I discovered this trick in one of the historical FPGA CPUs more than 20 years ago.
A typical adder uses a "carry-propagate" circuit where two input bits of equal weight are combined to create a "generate carry" signal and a "propagate carry" signal. Both are the result of a very simple boolean operation :
- Generate is created by AND
- Propagate is created by OR
See what I see ?
These operations can be factored and shared between the adder unit and the boolean unit. The only gate to implement separately is XOR... which can be derived from the already computed OR and AND ! This XOR is in turn used in the last stage of the adder.
This method is implemented in the ALU of #YGREC8 at the gate level and it works very well. Look at the VHDL source code and the logs :-)
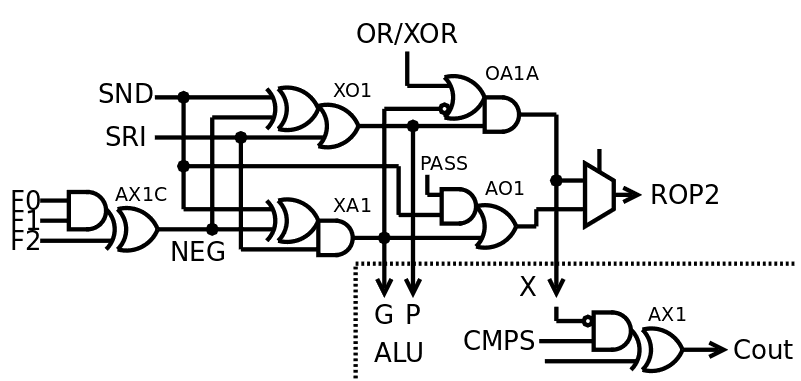
This diagram doesn't look at all like those at the top of the log, but now you can see why and how it is more efficient.
 Yann Guidon / YGDES
Yann Guidon / YGDES
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.