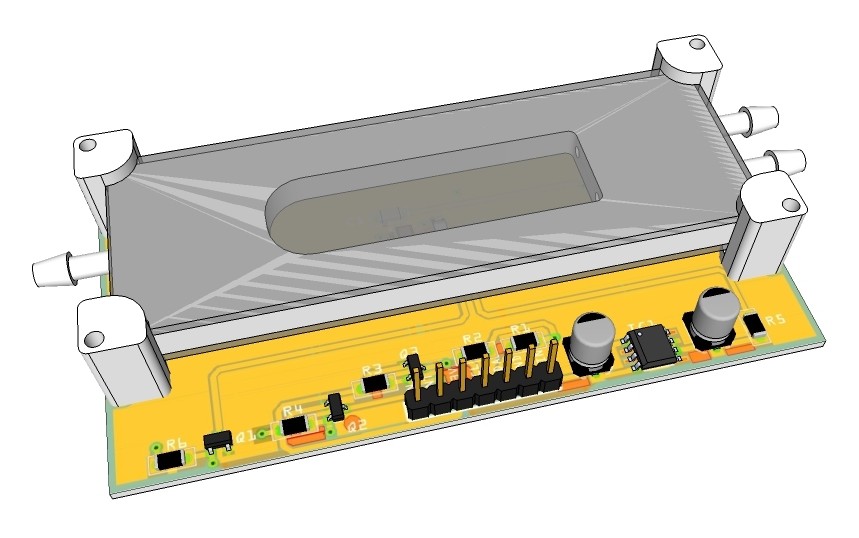
As mentioned already under "Project details" I am planning to add a Lab-on-a-chip system as a peripheral device for the medical tricorder. It is basically a photometer/color sensor mounted beneath a translucent micro reaction chamber with two inlets for the reagents and one outlet for the waste. The volume of the reaction chamber is approx. 1.87 ml.
So far I have designed the 3-D printed parts and PCB and sent them off to the fab house. Below rendering shows how the LOC will look like.
Schematics:
I am using a TCS3472 color sensor. The mosfets Q2/Q3 (BSS138) building a logic level shifter for the 3.3V/5V I2C bus. R1 to R4 are the required pullup-resistors for the I2C bus. R6 is the pullup resistor for the gate of Q1, R5 is used as the series resistor for LED1. MC 33269D-3.3 is a low dropout, 800 mA positive voltage regulator. It requires an output capacitor of at least 10 μF for stability. As it is recommended I added an input capacitor with the same value as well.
Routed PCB: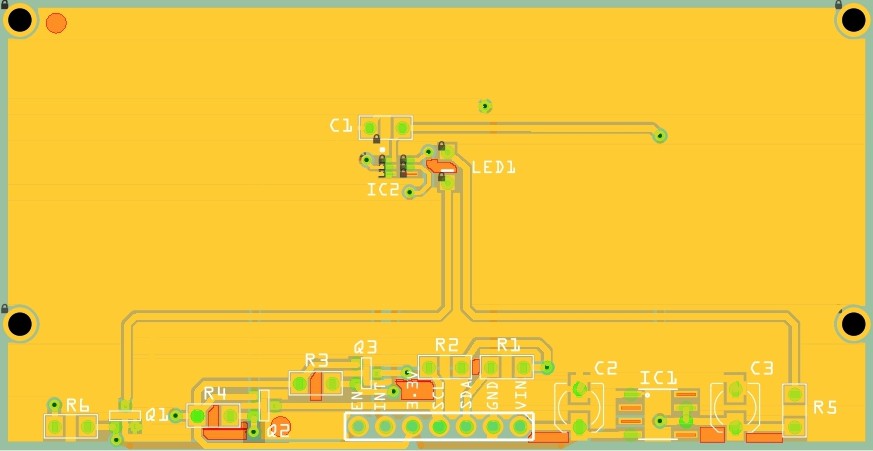
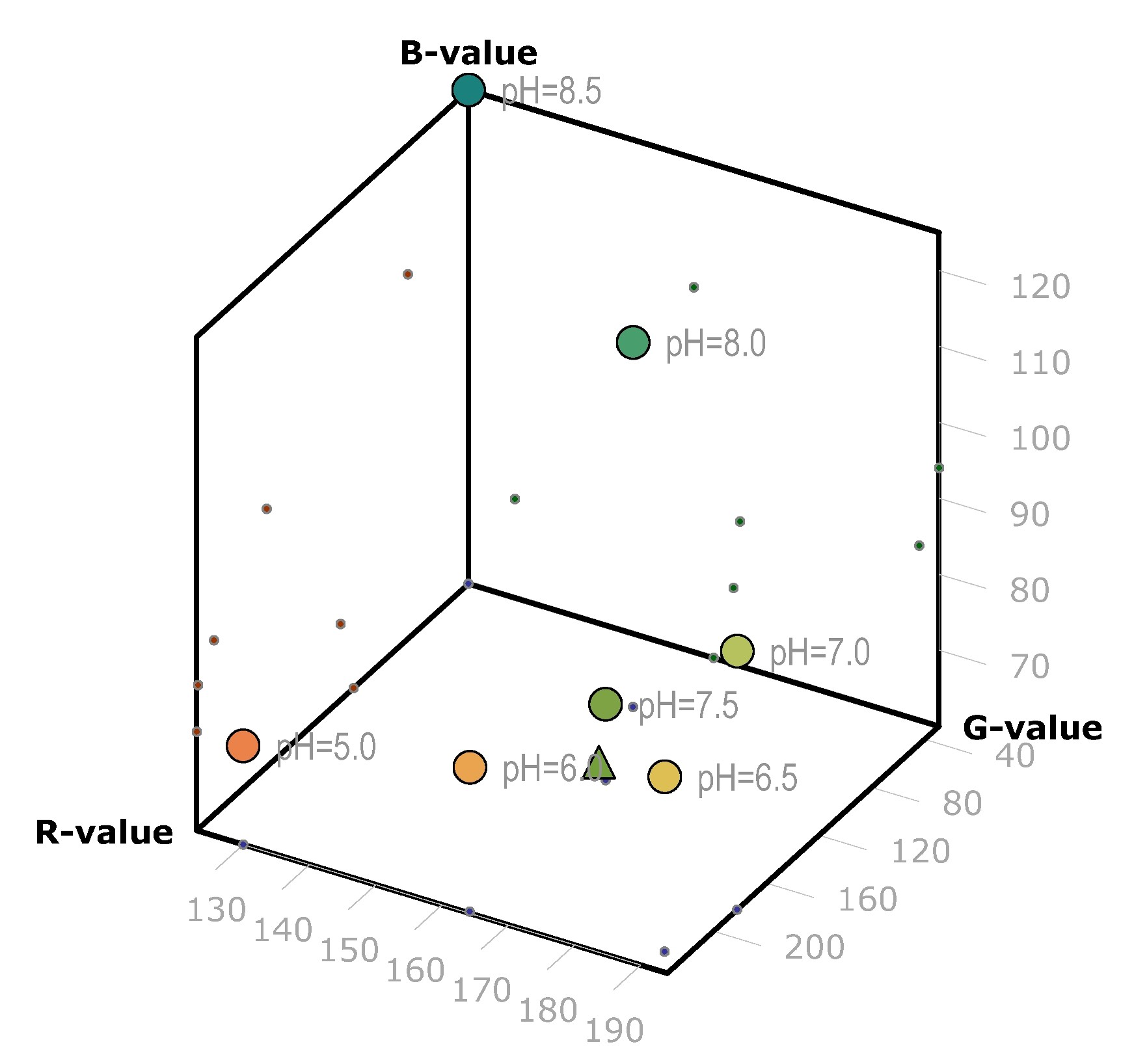
I will use the k-NN (k-nearest neighbors) algorithm, one of the simplest of all machine learning algorithms, to classify the detected color and assign it to the concentration of the detected substance, e.g. glucose via Trinder glucose activity test:
As the training set of colors associated to the concentration of a certain substance will only contain one sample per color, k = 1. And as we have RGB values, we will work in a 3-dimensional Euclidean space. So all we have to do is to find the smallest Euclidean distance from the sample point to any of the training points.
In general, for an n-dimensional Euclidean space, the Euclidean distance between two points
and
is given by
Example pH. The triangle shaped-point is a new sample which needs to be classified. In this case the nearest neighbor is the point with the marker 'pH=7.5.
 M. Bindhammer
M. Bindhammer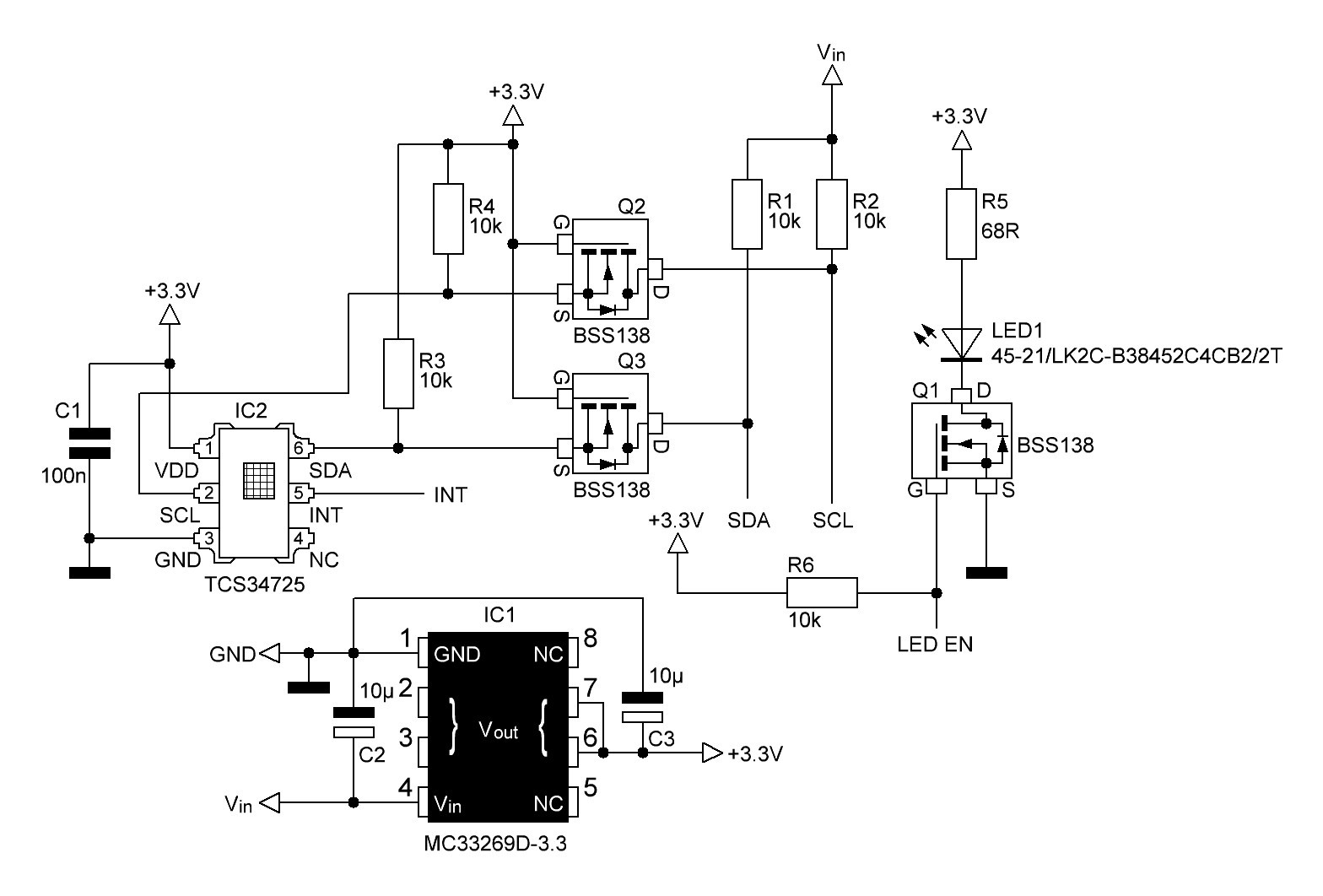
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.