The flip-dot infection has spread and there is no cure so let's go with it.
The Tetris game is a pretty cool application but then, @menguinponkey started #Game of Life on DIY TTL CPU 'S.A.M.I.R.A.' and... Do I need to explain in details ?
OK I will :-)
Conway's Game of Life.
@Shaos informed me that there is one flip-dot GoL exhibition at the NYC Hall of Science but I can't find pictures online. And it can't be great because I haven't designed it ;-)
So I'm thinking about an algorithm to efficiently compute it on the 8-registers relay computer but none of the classical computation algorithms fit. I'm one of those fools who think they can do better than Michael Abrash's awesome "Zen of Code Optimization" book.
You see, I'm a very long time fan of cellular automata. I could program one on a 286 PC with DOS's DEBUG.EXE. And I have read Michael's book. I have seen the revelations. I have applied the principles and used them in my Master's Thesis, doing interactive fluids simulations on millions of particles with a Pentium MMX PC.

I used "lateral thinking" to go 2× faster than the fastest program I could find. I squeezed it to the last cycles and developed optimization tools that boosted other projects. So I know a few things about how to compute efficiently and #AMBAP: A Modest Bitslice Architecture Proposal has barely enough resources to do it so let's squeeze again :-)
Looking back at the GoL rules, I found familiar structures that I had optimised 15 years ago, but this time it would be with 16-bits words, not 64-bits MMX registers.
Let's start with the definition:
An orthogonal 2D array of bits has states 0 (dead) or 1 (alive). Each bit has 8 neighbours (lateral and diagonal).
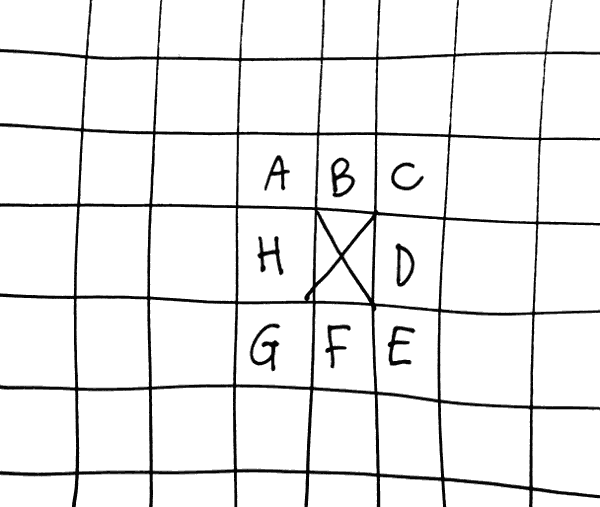
Take any bit, call it X (that's my convention). To compute the state at the next time step, count the number of neighbours that are alive then
- If X=1, clear to 0 if the count is not 2 or 3
- if X=0, set to 1 if count is 3
From there on, every algorithm I see on the Rosetta site simply counts the neighbours. It's the definition, right ? Been there, done that, highly inefficient :-D I know I come late to Abrash's coding contest but there is a big opportunity for lateral thinking, which I successfully applied to the FHP3 model.
The key is to process as many sites as possible with boolean instructions, using very wide registers. This becomes a matter of boolean optimisation and the computation uses very few branches/jumps.
One of the annoying parts of GoL is the accumulation of the neighbours. However, with a bit of help from a different layout, it appears that a lot can be factored.
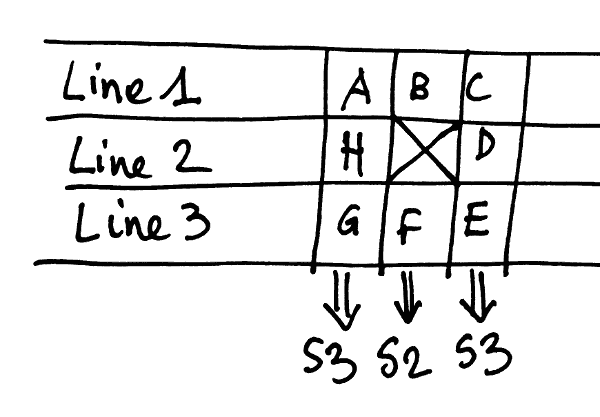
Let's define S2 the sum of the North and South neighbours. From there we can define S3 as the sum of the three East or West neighbours. If we consider that this sum can be computed "laterally", with one bit of the sum in a different register, it's obvious that we can derive S3 from S2 with a simple bitwise addition and S3 can be reused for the computations of the left and right neighbours. There is a lot of potential reuse !

Things are pretty obvious now (at least for me). The next question is : how to compute a sum ? Very easy ! S2 is a classical half-adder and S3 is a classical full-adder :-D
But now, S2 and S3 require more than one bit^Wregister to hold the 2-bits sums. Let's call them S20, S21, S30 and S31 (the last digit being the order of the bit).
; half adder:
S20 = L1 ^ L3;
S21 = L1 & L3;
; full adder:
S31 = L1 | L3;
S30 = S20 ^ L2;
S31 = S31 & L2;
S31 = S31 | S21;With 6 CPU instructions, I have computed 16 3-operands additions with partial results !Less cycles than the number of neighbours, who can beat that ?
The less easy part is how to combine these values efficiently. A sum of 8 inputs gives a number between 0 and 8, 4 bits are required and the number of registers explodes. So let's look back at the rules.

The interesting part is when S0=S1=1 and the output is set to 1. That's a simple AND there.
The lower half of the table can be simply discarded so no need of a 4th bit to encode 8. Instead, bit S2 is considered as an "inhibit" bit.
Using this inhibition trick, the combination with the previous X state is quite easy : before ANDing S0 and S1, X is ORed with S0 to "generate" the expected pattern 11.
X' = (S1 & (S0 | X)) & ~INHNow the challenge is to compute a "saturated population count", out of full adders.Things start easy with bit 0, it's a simple full adder.
S0 = X | ( S30<<1 + S20 + S30>>1 )I include X in the computation as soon as possible so its location can be used as a placeholder/temporary variable later on :-) The register pressure is extreme in AMBAP...The destination can also use the location of the S20 operand. The left and right shifts are a compelling motivation to insert the operations just in front of the ALU. x86 will use the "LEA" instruction instead, ARM will be happy too.
S0 = S30<<1 ^ S20;
S0 = S30>>1 ^ S0;
S0 = S0 | X;So S0 can now be located in X. But that's only the LSB and the carry is missing.
S0C = MAJ(S30<<1, S20, S30>>1);
= ( S30<<1 & S20 )
|( S30>>1 & S20 )
|( S30>>1 & S30<<1)
= ( ( S30<<1 | S20 ) & S30>>1 )
|( S30<<1 & S20 ) I have chosen the commutative operands such that there is only one shift per instruction. The computations are basic but the register pressure it very high so variable allocation is critical. S20 will not be reused so it can hold one temporary value after being used.
S0C = S30<<1 | S20;
S20 = S30<<1 & S20;
S0C = S30>>1 & S0C;
S0C = S0C | S20;S30 is free, now, as well. It can be renamed to S1...
Things are getting ugly now. We have four inputs, not 3, so the typical full-adder can't be used. The operands are S0C, S21, S31<<1 and S31>>1. At least, the LSB (S1) is easy to compute, it's a bunch of XOR:
S1 = S31<<1 ^ S0C;
S1 = S31>>1 ^ S1;
S1 = S21 ^ S1;The magic happens with S1C, which is actually the inhibit signal. We don't need to compute an accurate, multi-bits result and this saves some instructions... And since we're not building an actual circuit, we can favor "long latency" over "immediate result", such that a result is progressively computed, instead of using a lot of temporary registers. But first, let's look at the truth table:

What becomes apparent is that the inhibition output is set to 1 when more than one input is 1. INH is cleared when only one, or zero, input is set. It's a sort of OR where we "forget" the first 1. There are several approaches to that but only the most computationally spartan is interesting. I decided to reuse the previous approach of splitting things into half-adders and here is the result :
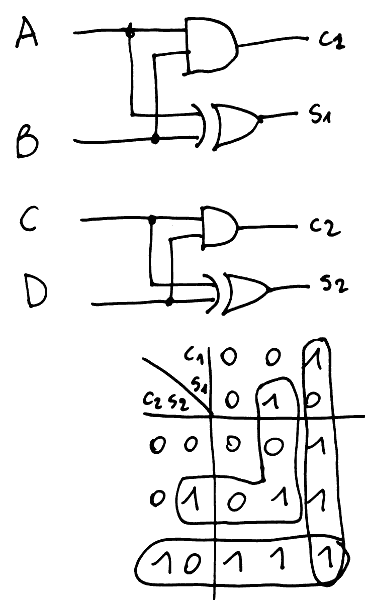
The result is 1 when either the Cs are 1, or S1 and S2 are 1.
INH = S31<<1 & S21; (C1)
S1_ = S31<<1 ^ S21; <- S21->S1_
C2 = S31>>1 & S0C;
INH = INH | C2;
S2_ = S31>>1 ^ S0C;
S2_ = S2_ & S1_;
INH = INH | S2_;There, there...
The rest is pretty straight-forward.
.
.
.
More algorithmics at #Game of Life bit-parallel algorithm since this project is initially a HW project :-D
 Yann Guidon / YGDES
Yann Guidon / YGDES
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Fluid dynamics seems to impart a certain way of thinking on optimizing code, one that seems to be taboo among many other programmers, which is "Optimize the algorithm for your usage case before writing the code" mayhap this is why this hasn't surfaced until now?
Are you sure? yes | no
I don't have a clue. I have roots in industrial electronics and I lean toward scientific HPC... I am a lousy application writer but I know how to saturate a CPU's pipeline.
Are you sure? yes | no
Well the fluid simulations as a previous work, and the actual notes seem to indicate that you follow that train of thought, whereas I have been yelled at because I'm apparently supposed to "Write code first and optimize later".
Are you sure? yes | no
It depends on the context, of course.
For the record, I'm bad at writting applications...
Are you sure? yes | no
Scientific computing has a particular advantage : years and years of iterations over a "simple" case, many people working on a pretty well defined problem for a long time, which has given pretty incredible solutions.
For example my research has found papers mentioning the "lateral" approach in the 80 or 90 on vector supercomputers, for a very early version of the FHP model. I did "rediscover" it and enhanced it with interactivity (Cray jobs are rarely interactive but a PC is). I also use the more efficient FHP3 model (better viscosity) and added dynamic generation of walls.
Knowing this, I'm still surprised that I have never seen any other implementation of a lateral algorithm for other cellular automata. Maybe the wider availability of 64-bits platforms was a critical ingredient but come on, we've had MMX for 20 years now...
Are you sure? yes | no
LOL: "And it can't be great because I haven't designed it" :)
And... Wow!
Are you sure? yes | no
Look, mommy ! no coffee !
:-P
I just tested the equations with a small JS program and ... yes, WOW.
Are you sure? yes | no
If this shizzle works, yo... Seems like you've revolutionized the GoL!
Are you sure? yes | no
Spoiler alert : it works.
L2=world[i];
L1=world[i-1];
L3=world[i+1];
// Parallel additions
// half adder:
S20 = L1 ^ L3;
S21 = L1 & L3;
// full adder:
S31 = L1 | L3;
S30 = S20 ^ L2;
S31 = S31 & L2;
S31 = S31 | S21;
// Sum's LSB
S0 = (S30>>>1) ^ S20;
S0 = (S30<< 1) ^ S0;
// LSB Carry
S0C = (S30<< 1) | S20;
S20_= (S30<< 1) & S20;
S0C = (S30>>>1) & S0C;
S0C = S0C | S20_;
// Sum's middle bit
S1 = S21 ^ S1;S1 = S31>>>1 ^ S0C;
S1 = S31<<1 ^ S1;
// Inhibit
S1_ = S31<<1 ^ S21;INH = S31<<1 & S21;
C2 = S31>>1 & S0C;
INH = INH | C2;
S2_ = S31>>1 ^ S0C;
S2_ = S2_ & S1_;
INH = INH | S2_;
X2 = S0 | L2;
X2 = X2 & S1;
X2 = X2 & ~INH;
BAM. Your new row's value is in X2.
I didn't revolutionize anything, it was there all along, waiting to be done. I can't believe that it's not a common algorithm for a long time already...
Are you sure? yes | no