Parallax is the bane of point-and-shoot cameras, particularly ones with a lot of separation between the lens and the viewfinder. This is the case with the SQ6, which has numerous moving lens and film processing parts separating the objective and viewing optical paths. Cameras like the Instax Mini 90 have a fancy parallax correcting viewfinder, but users of the SQ6 are not even graced with the presence of correction lines. The user manual makes some reference to the camera needing to be shifted up and to the right while shooting nearby subjects, but there’s hardly anything quantifiable to glean from that statement. In my teardown of the SQ6, I noticed that the viewfinder is actually already angled down and to the left, to compensate for some of that error at the minimum focus distance. However, this exacerbates parallax error at distances beyond around 2 meters.
So all that begs the question – how are you supposed to reliably center photos with the SQ6? A bit of trigonometry holds the answer.
First, let’s consider the phenomena of parallax. Parallax error occurs because the image-taking path is not collinear with the viewing path. In our case with the SQ6, the paths are askew – they intersect at a given distance, but diverge elsewhere. At distances besides the “ideal” viewing distance, the lens and the viewfinder are aimed at different targets.
Suppose the viewfinder is angled towards the optical axis by an angle theta with an offset between the lens and viewfinder of a_o. Then, the ideal viewing distance, at which the viewfinder and objective axes are aligned, is:
I have measured the angle of the viewfinder as about 1.57 degrees, and the horizontal offset of the lens and VF as about 65 mm. Thus the ideal viewing distance is 2.4 m. For objects closer than this, you must tilt the camera up and to the right, for it to be centered. For objects further away, the camera must be tilted down and to the left. But by how much exactly?
In the above example, we would need to point the camera 2.2 degrees to the right to center the image correctly. All of this is well and good, but have you ever tried to move a camera precisely 2.2 degrees? It would be more helpful if we could quantify the actual amount of parallax correction needed, in the viewfinder.
By my estimates, the viewfinder spot (the little etched ring used for aiming) of the SQ6 spans about 5.7 degrees. So, in the previous example, when focusing on an object 1 meter away, you would have to shift the image in the viewfinder .38 spots up and to the right. Or, refer to this handy dandy plot, generated with the above equations. You would shift the viewfinder such that the center of the target object aligns with the dot marked “1m”.
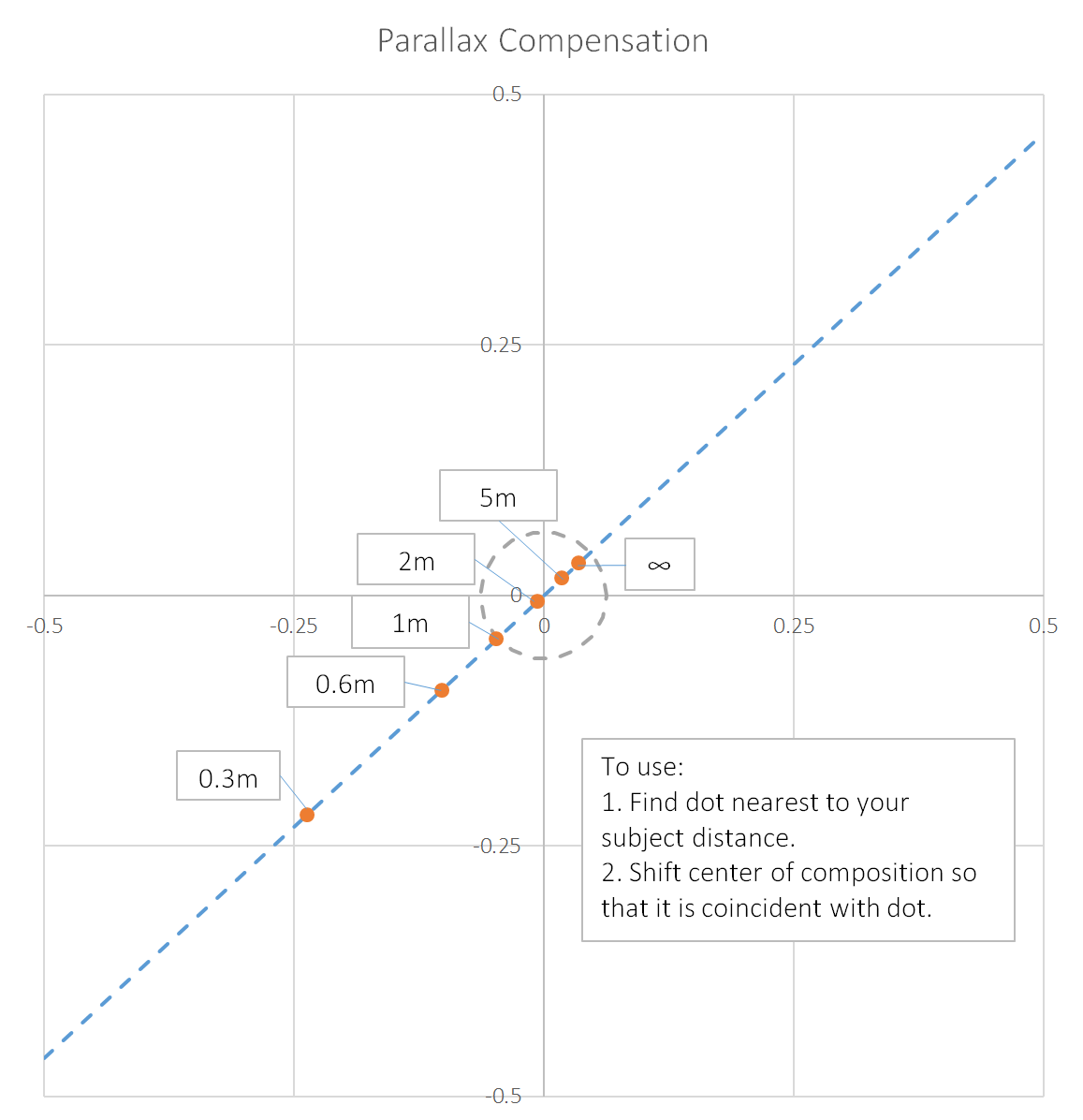
This is no substitute for a fully-parallax corrected viewfinder. But it’s a start! It’s a simple enough reference that you could print out a little copy and stick it to the back of your camera. I would do that, but mine is in pieces.
 Kevin Kadooka
Kevin Kadooka
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Nice one! One oberservation though, where in your graph it shows to offset it within the circle, my circle has to be completely to the left of the object instead to even come close to centering the object. Any clue what would cause this? Simply a different angle in the viewfinder or..?
[Edit]
Might also be the distance from my eye to the viewfinder, not sure. Will test this later today if that makes a difference. So far it's still a bit hit-or-miss when it comes down to figuring out the offset.
Are you sure? yes | no