We started the project by slicing the body of a Nerf Vortex foam football in half with a box-cutter. We chose this particular football because it was cheap, stable during flight (due to the dart-shaped tail) and easy to mount electronics in. The ball had three whistles mounted along its perimeter; we removed one to make room for the electronics. 

We had two goals: measure the acceleration of the ball during the throw (which is used to calculated distance thrown) and measure the centripetal acceleration of a point on the ball (which is used to calculate angular velocity). 

We needed to use two accelerometers, as it's impossible to distinguish linear acceleration from centripetal acceleration given a single acceleration vector.

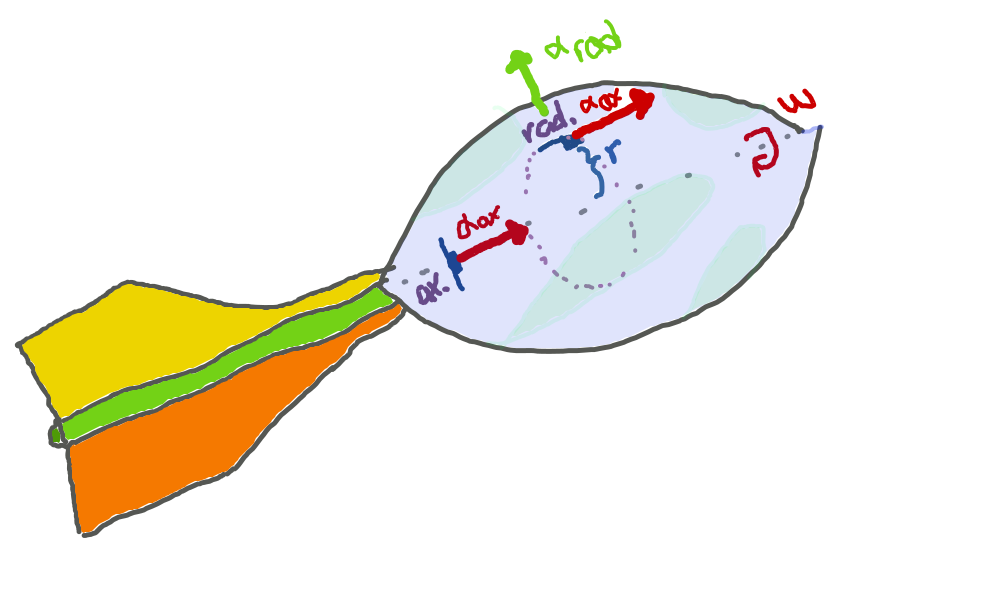
We mounted one of the accelerometers along the axis of rotation, taking great care to place the accelerometer chip as close as possible to the spin axis. This was our axial accelerometer, which would be unaffected by centripetal acceleration during flight (at least in theory).

We began by calculating the initial velocity of the football. This was done by integrating the magnitude of the football’s axial acceleration during the throw (from start time to time of release) and subtracting the acceleration due to gravity.

Next, using the angle at which we threw the football (with respect to the horizontal) we calculated the horizontal component of the ball's velocity:

and integrated it once more, from time of release to time of catch.

This double-integration is a direct application of the fundamental theorem of calculus to bring us from the realm of accelerations (measured in meters per second per second) to the realm of distances (measured in meters). The accuracy of this method is severely limited in the long run, as any errors in the accelerometer readouts tend to be magnified over time and result in greater and greater drift in the absence of absolute positioning data. However, this dead-reckoning method can be decently accurate -- most ICBM's rely on precise accelerometers and gyroscopes to calculate their location and bomb the right targets!

The other accelerometer was mounted two centimeters away from the spin axis in the widest part of the ball, normal to its surface. This was our radial accelerometer, which would experience a great deal of centripetal acceleration during flight. 

We took the magnitude of the radial accelerometer's data, which eliminated the effects of position on the acceleration readout. This calculation is done on data points collected in mid-air, where the centripetal acceleration is the only significant component of the radial acceleration vector (no gravitational acceleration, negligible tangential acceleration, negligible linear acceleration)

Using the angular acceleration and radius of rotation (the radial accelerometer spins in a four-centimeter-wide circle) we calculated the linear velocity of how fast the ball spun: 

Finally, we divided the linear velocity by the radius to determine the angular velocity of the football.

The setup runs on a NodeMCU with an ESP8266 processor. We chose this microcontroller because of its low profile (no through-hole components or headers) and built-in WiFi modem.

• The NodeMCU has a 3.3 volt logic level, unlike the Arduino Uno’s 5 volts. Fortunately, all our components ran fine on a reduced voltage, though the beeper was quieter.

Two MPU6050 digital accelerometers were attached to the I2C bus on the NodeMCU. 

• The accelerometers have a default address of 0x68, which would’ve caused an address conflict, so we shorted the AD0 pin to 3.3V on one of the accelerometers to switch its address to 0x69.
• These accelerometers are configured, by default, to a range of +/- 2 g (~20m/s^2) of acceleration per axis, but are capable of measuring +/- 16 g (~160 m/s^2) of acceleration. As our project would deal with abrupt changes in velocity, we switched the accelerometers...