Introduction
Out of curiosity I tried replacing the base resistor in my 5-stage ring oscillator with a red LED. Why would I do that? Well, first of all the footprint of the LED and resistor exactly matched on the PCB. So why not?
There was a bit more rationale behind this, though: The LED will increase switching voltage and should improve noise margin, similar to what I did with "LTL". Since LEDs have a non-negligible internal capacitance, I was also hoping that the LED would act in a similar way as the reach-through capacitors in parallel to the base resistor, as I tried earlier.
What started as a quick experiment turned into quite a curious feat, as you will notice later.
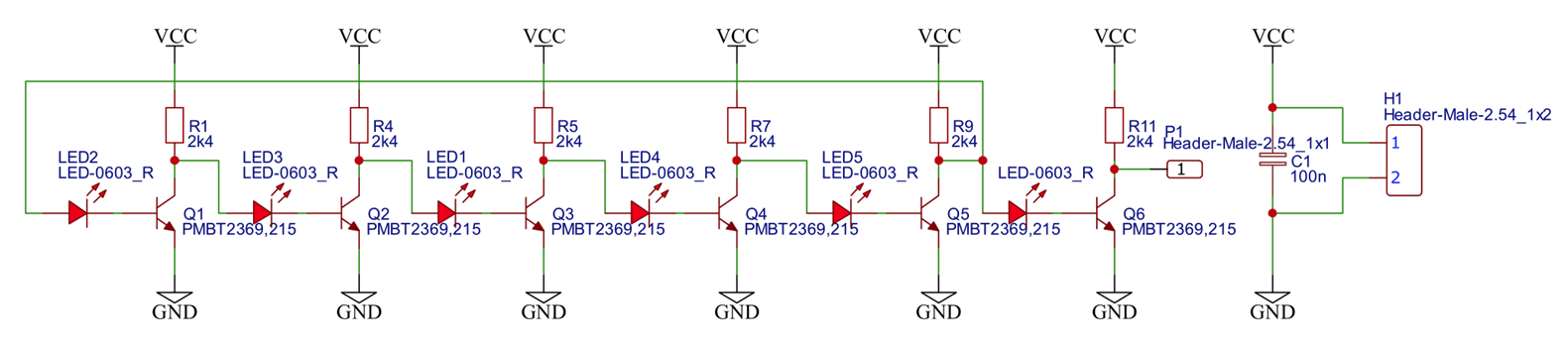
The schematics are shown above. Please ignore the resistor values, I used 470 Ohm collector resistors in all cases. I built two versions: One with PMBT2369 and one with PMBT3904.
PMBT2369 based RINGO5
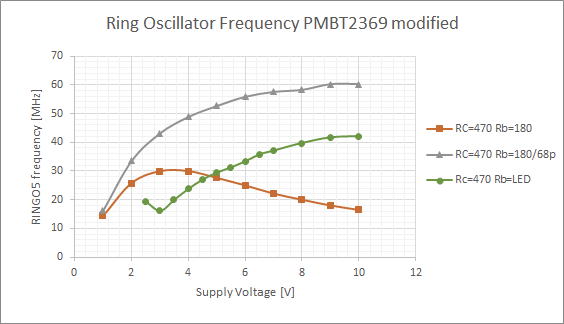
- Oscillations are only observed at a much higher operating voltage of ~2.2V instead of 1V for the others devices.
- The frequency is continuously rising with the voltage, no maximum is visible within the voltage range.
An increased operating voltage is expected since the additional voltage drop over the LED increases the turn on voltage of each inverter. The larger swing of the logic levels also leads to a reduction of propagation delay and hence oscillator frequency.
The absence of a frequency maximum and the higer maximum frequency compared to the normal ring oscillator without reach-through capacitor (orange) suggest that the LED capacitance does indeed act in a similar way as the parallel capacitor.
It seems that both initial assumptions have been confirmed. Does it mean that RTL with LED-instead-of base-resistor is the way to go? Probably not, as there will be serious issues with device matching when multiple gates are connected in parallel due to variation of LED forward voltage and transistor VBE. This is addressed in the LTL gate, however.
PMBT3904 based RINGO5 with LED instead of base resistor
Ok, let's repeat the same experiment with the "standard" switching transistor PMBT3904.
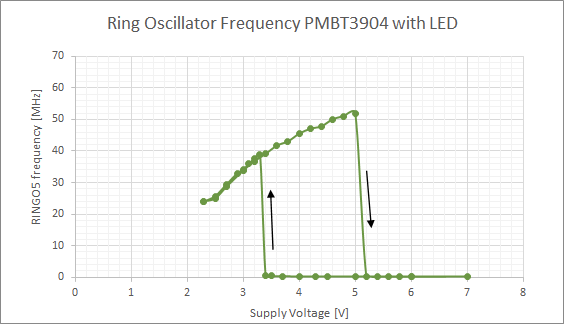
The plot above shows the ring oscillator frequency when sweeping the voltage up to 7V and then down again. There were quite a few surprises. First, the maximum frequency is above 50MHz, far above anything I had measured with the PMBT3904 before. Then, and this is even more suprising, above 5 V the frequency suddely drops to a very low value below 0.5 MHz - 100 times lower. When the voltage is lowered to below ~3.5 V, the frequency increases again.
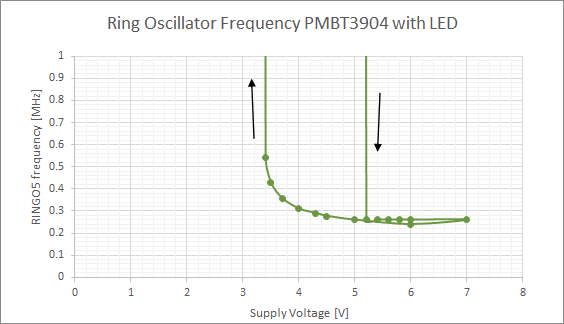
The low frequency region is shown in more detail in the figure above.
It is clear that the frequency shows a hysteretic behavior in respect to the voltage sweep. This means that the circuit has two stable operating points between 3.5 V and 5 V - one at low oscillating frequency and one at high frequency. Some waveforms details are shown below.
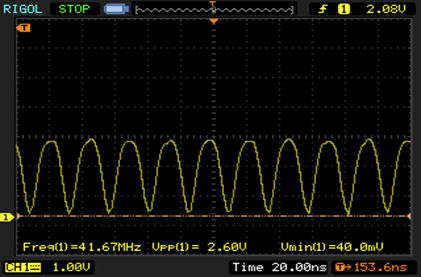
Waveform of the high frequency oscalliating mode.
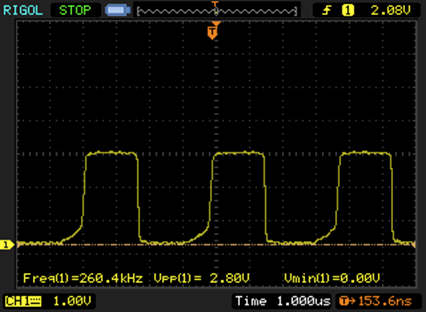
Waveform of the low frequency oscillating mode. You can clearly see fully saturated switching.
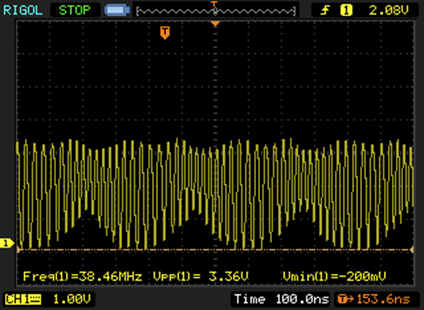
Waveform in the high frequency operating point close to the switching point. One can see that several frequencies are superimposed and the oscilation gets instable.
This result is quite weird. In one mode, the oscillator is much faster than any PMBT3904 based oscillator i built before, in the other mode it is incredibly slow. What is the exact mechanism behind the metastability? Can it be used for something?
Spice Simulations
I set up a Spice model in LTSpice to understand better what is going on. See below for the schematics. One big source of inaccuracy is the LED model itself. I took a model for a similar LED from the OSRAM OS homepage and modified it to fit the LED I used (some noname 0603 SMD LED). However, I am certain that there are lots of inaccuracies. I doubt there are many spice model for LEDs out there that exactly model transient behavior.
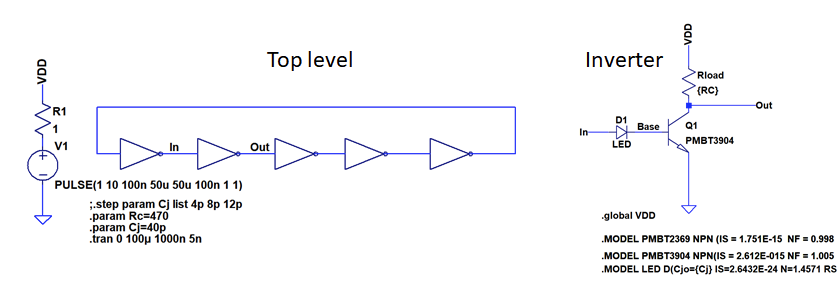
For this circuit, the most relevant parameter in the LEDs seemed to be the junction capacitance Cj, hence I modified this throughout my investigation.
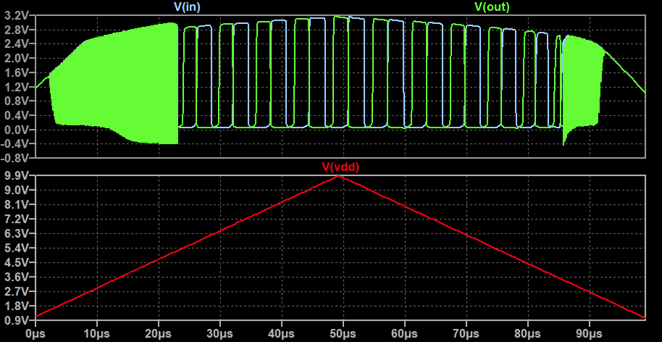
I set up the model as a transient simulation that sweeps VDD. You can see the result above. The upper pane shows the voltage at the input and output of one of the inverters withing the ring oscaillator. The lower panel shows the supply voltage over time.
The metastable behavior is also reproduced in Spice. There is a clear distinction between fast and slow oscillating mode and the transition voltages between these depend on sweep direction.
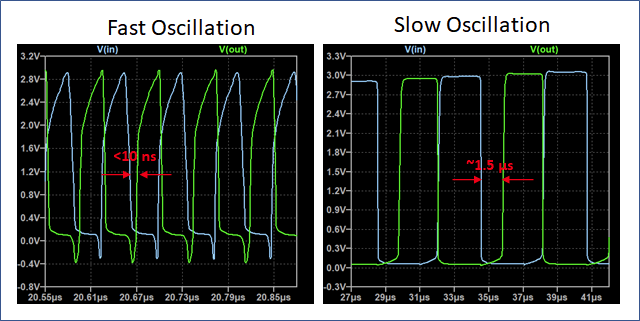
Looking at the detailed input-output relationship of the inverter already shows some differences: When the input goes hi, the output is immediately pulled to low, both in fast and slow oscillation mode. Things are quite different for that falling edge of the input signal: In slow mode, that output rises with a delay of almost 1µs, while it almost immediately risis in fast oscillation mode.
This suggest that the slow oscillation mode is dominated by base saturation charge storage time, while this is somehow eliminated for the fast mode. Please note that also in the fast mode, there is full saturation switching going in, the transistor is fully turned on and off as can be seeen from the voltage swing.
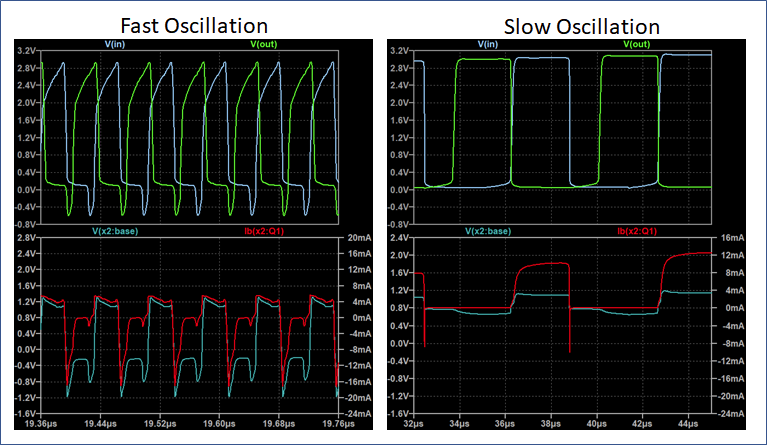
This is not the case for the slow oscillation. An addtion, the positive base current is much higher for slow oscillation, which means that even more saturation charge is build up.
These results seem to explain the bahavior from a phenomenological point of view. It is not quite clear, however, what compels the circuit to switch into one mode or another? One reason could be that the fast oscillating mode needs a high frequency input signal to avoid build up of too much saturation charge and for the negative overdrive to work. Since the circuit is circular, this operational mode is self sustaining.
As an interesting addendum: One critical factor for the behavior of the oscillator is the junction capacitance of the LED. I assumed a junction capacitance of 40pF for the simulations above, which may be on the high side for a 0603 SMd LED.
A smaller junction capacitance increases the frequency of the fast oscillation, while a larger does decrease it. Furthermore, a larger capacitance improves the stability region of the fast oscillation mode.
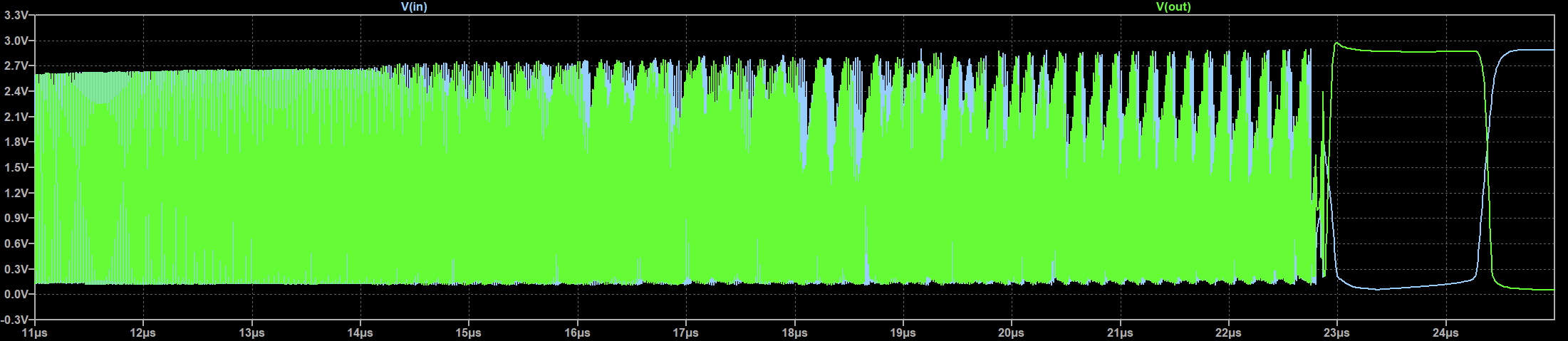
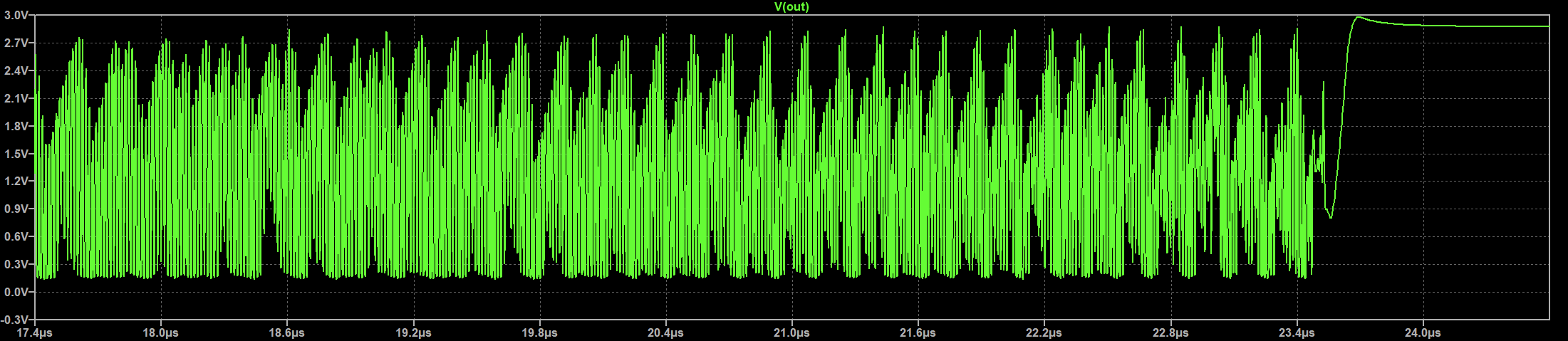
When reducing Cj to 6 pF (first panel above) or 4 pF (second panel), a notable region of instability with several frequency components is observed close to the transition, similar to what I observed in the actual circuit. This behavior appears to be unpredictable and could point to chaotic behavior of the system, as observed, for example, in the van der pol oscillator. Varying the junction capacitance to other values has somewhat unpredictable results. It is not quite clear to me, what the governing parameters of this system are. More simulations would be needed.
Summary
Using a LED instead of a base resistors help increasing the switching threshold and had a speed-up effect on the ring oscillator for the PMBT2369 and the PMBT3904. It was, however, observed that the PMBT3904 ring oscillator had two or more metastable operating conditions that are interesting, but not completely understood, and could introduce instability into any circuit using this approach. This would be especially relevant of the input signal is not well controlled. Using a LED instead of a bases resistor is therefore not really recommendable.
The PMBT3904 ring oscillator exhibits a region of instability that may point to chaotic behavior, the underlying effects are not understood so far.
Addendum - Trajectory Plots
I used the X-Y functionality of my oscilloscope to plot the trajectories at different supply voltages to test the hypothesis that the ring oscillator is not only metastable, but also a chaotic system, as also suggested on µC.net by Andreas.

The test setup is shown above, for the sake of completeness. I tapped into two output nodes that were spaced two inverters apart. Assuming that the phase delay through the entire ring oscillator is 180°, we shold observe a phase shift of 2*180°/5=72°, which means that we shold see a slightly elliptic circle if the oscillator generated a pure sine. In the investigations above, I connected the oscilloscope via an output buffer (rightmost inverter on the PCB) to create a constant loading.
Since I needed to tap two places in this case, I have to directly probe the oscillator. The additional capacitive loading of the two probes on the ring oscillator led to a shift of the transition voltage from high to low frequency mode to above 7V. The general characteristics of the setup remained the same, though.
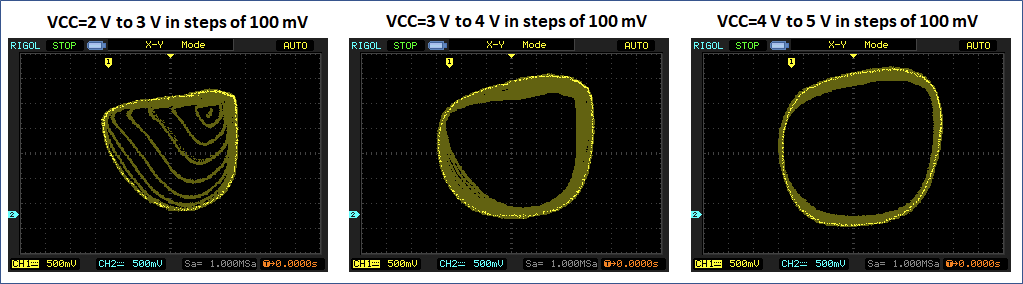
The plot above shows trajectories from 2 V to 5 V supply voltage in steps of 100 mV overlaid. In this range, the oscillator shows stable operation with limited noise. The shape of the trajectory changes due to a change in rise- and fall-times with voltage and due to smoothing caused by the limited bandwidth of the oscilloscope.

Things start to get interesting at 5.3V. Here we can see that the oscillation becomes instable, looking like noise is overlaid. However, at 5.7 V and 6.1 V we can see two stable complex trajectories that suggest the presence of limit cycles. 6.2 V is unstable again, 6.5 V shows a drastically changed trajectory.

Again, clear limit cycles at 6.8 V, 7.1 V and 7.3 V. At 7.5 V the oscillator finally switches to the low frequency mode.
All in all, even though I am not an expert for nonlinear systems, this looks very much like a chaotic oscillator to me.
There are many other chaotic circuit out there, like Chuas circuit. Typically nonlinearity is introduced by a nonlinear resistive element, like a diode. What seems intriguing about the ring oscillator investigated here, is that it appears to introduce a nonlinear timing element in form of the base saturation charge.
 Tim
Tim
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Is this the same "something... allows them to switch very quickly... this "magic quality" wears off, and they switch slowly again." effect Ted Yapo writes about at https://hackaday.io/project/19333-cbjt-logic/log/52084-no-its-not-that-fast ?
Are you sure? yes | no
I would assume so. Basically the base is connected with a high impedance that is shunted with the diode capacitance. If you have a fast rising edge at the input the base will switch quickly, if the input slew rate is low, the base will charge to saturation.
Are you sure? yes | no
That's a very instructive write-up. Thanks!
Are you sure? yes | no
Wait... if you can do chaotic oscillations at such high speeds, then you *could* create a very high speed true RNG with more boards ...
Are you sure? yes | no
That's actually a really cool idea!
I googled a bit around. One point that was made, was that chaotic oscillations, while being unpredictable, actually follow a pattern, the attractor- While the pattern may be unpredictable, it will still be a bad source of random numbers. So maybe there is no benefit in the end..
Here is a random number generator based on PMBT3904: (Fig 20)
https://www.nutsvolts.com/magazine/article/bipolar_transistor_cookbook_part_5
It's using avalanche/shot noise of the emitter/base junction.
Are you sure? yes | no
Nobody would use unfiltered analog inputs as entropy sources ! the LEAST you have to do is follow it by a cascade of LFSR to spread the data even more and wipe the patterns out. This is because the analog source is too sensitive to external aspects : temperature, voltage, even ambient light...
The point with your circuit is that you can output MUCH more entropy at 50MHz than something that varies between 100K to 1M and you have to measure down to the noise level.
With several independent rings (with varying sizes to prevent crosstalk & correlation) you have > 100Mbps of entropy and then you filter it with cascades of LFSRs...
sounds like a plan.
If only it was possible with PMBT2369 ;-)
Are you sure? yes | no
Well, but one defining characteristic of chaotic oscillators is that their oscillation is locally correlated by the attractor? This was my concern.
On the other hand, searching for "chaotic ringo oscillator" yields a lot of papers where people try to introduce nonlinear coupling into linear ring oscillators to create instability and use this as a TRNG. (For example this: http://nlab.ee.tokushima-u.ac.jp/nishio/Pub-Data/PAPER/P052_Hosokawa-02.pdf)
I guess you are right and this could be used as a high rate TRNG. I guess the rationale would be that the chaotic behavior is indirectly used to amplify sources of randomness that influence its trajectory.
I wonder how to proceed from here? I could try to use a logic analyzer to sample a high rate bitstream. Some randomness evaluation would be needed then.
Are you sure? yes | no
You've been HaDed ! https://hackaday.com/2020/06/23/chaotic-oscillator-from-antique/
Are you sure? yes | no
Oh my...
Are you sure? yes | no