In the last log I showed a few computational issues:
- The motion primitives calculations are too slow (around 1ms after some initial optimization)
- The control function is too slow (around 250us)
- The control function is not called at a consistent rate (uses a software timer)
This log explains some updates I did to make things faster and more consistent. Some are still works in progress, but it is looking promising.
Pre-calculations
All of the motion primitives are set up as cyclical motions defined in Cartesian space. Both linear and quadratic Bezier curves are supported. I realized with typical control periods, and primitive calculation rates it would not be difficult to pre-calculate the positions, and then simply use a lookup-table when it is running to get the position. I implemented this right away. In addition, for simple position control through these profiles, inverse kinematics is required to calculate the motor positions. I also added a layer to pre-calculate the motor positions (in ticks, as integers). Now that everything was set up as simple integer lookup tables, motion primitives with position control are very fast. My timing showed that this calculation required only about 34us, around 30X faster than the original Bezier VMC setup.
Integer PID Controller
To make this control method even faster, I also had to set up the PID controller as integer only. Care must be taken when doing this, as it is easy to get odd rounding, overflow, and underflow issues with integer math. Thankfully, for position control my inputs and outputs were already scaled to be in the thousands typically, and the controller gains were reasonably high. Furthermore, the inputs were actually integers cast to floats, and the output was a float cast back to an integer. I therefore thought that I should be able to achieve decent control with a simple implementation. The code below shows the implementation. There are only two parts that are non-standard. First, the speed is filtered according to this great Hackaday project. In addition, my typical Ki for position control was 0.004. Therefore, I added an integral shift option so that effectively small Ki values are possible.
int32_t calculate_integer_pid(pid_integer_control_t * pid, int32_t setpoint, int32_t current_position)
{
static int32_t speed_old_z = 0;
int32_t error = setpoint - current_position;
int32_t speed_z = speed_old_z - speed_old_z >> pid->filter_shift + (current_position - pid->last_position);
pid->speed = speed_z >> pid->filter_shift;
speed_old_z = speed_z;
pid->integral += error;
if(pid->integral > pid->integral_max)
{
pid->integral = pid->integral_max;
}
else if(pid->integral < pid->integral_min)
{
pid->integral = pid->integral_min;
}
int32_t cmd = pid->kp * error + pid->kd * pid->speed + (pid->ki * pid->integral >> pid->integral_shift);
if(cmd > pid->cmd_max)
{
cmd = pid->cmd_max;
}
else if(cmd < pid->cmd_min)
{
cmd = pid->cmd_min;
}
pid->last_error = error;
pid->last_position = current_position;
return cmd;
}With this implementation used for position control, the position control loop is now about 79us, about 3X faster than before. More importantly, it seems to work just as well.
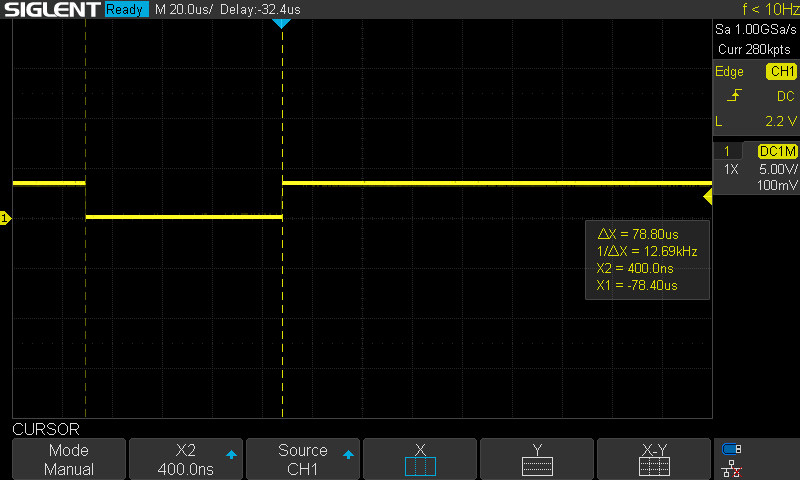
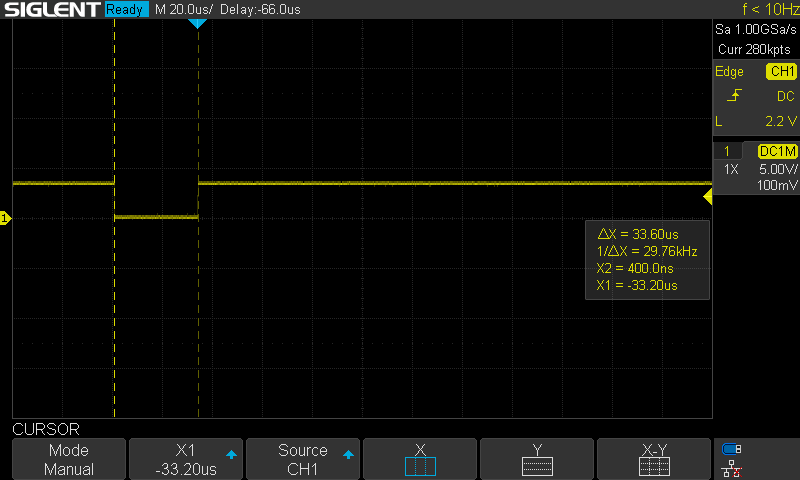
Hardware Timing
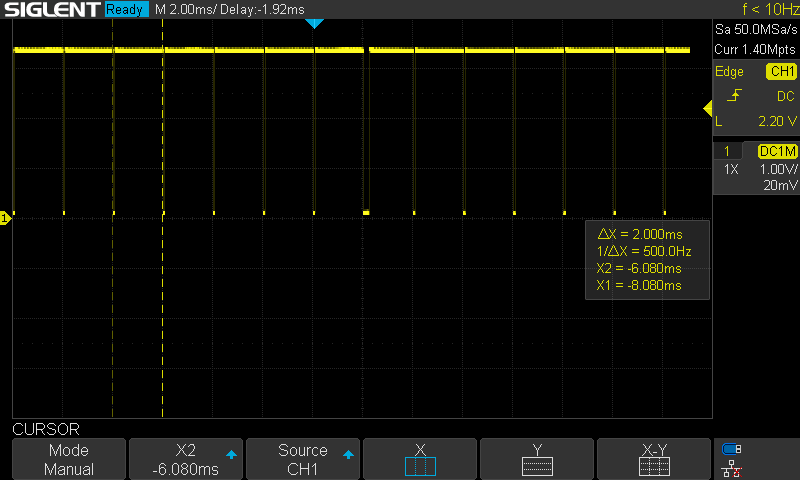
The control loop had been set up as a 500Hz FreeRTOS software timer. Although it worked OK for position or speed control, it likely isn't OK for current control. It is not fast enough, and the jitter is quite significant. I therefore set up a hardware timer. As a first test, I set it up to toggle a pin (with some busy delay) on every interrupt. This was quite consistent and accurate, as seen in the next two images.
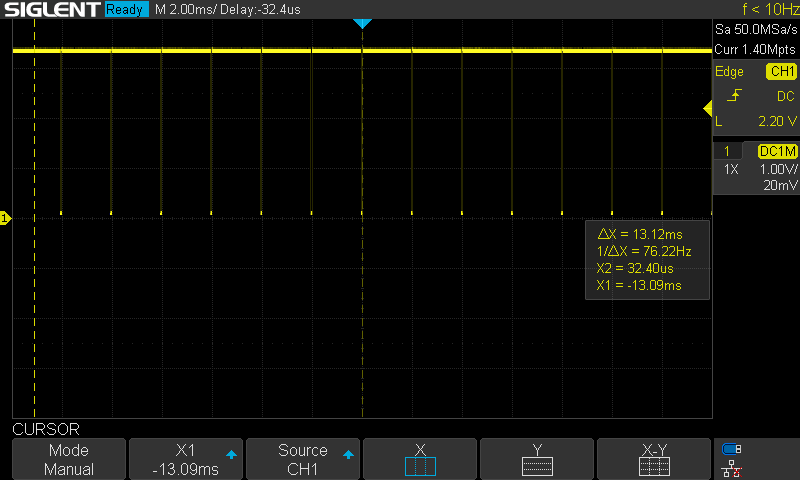
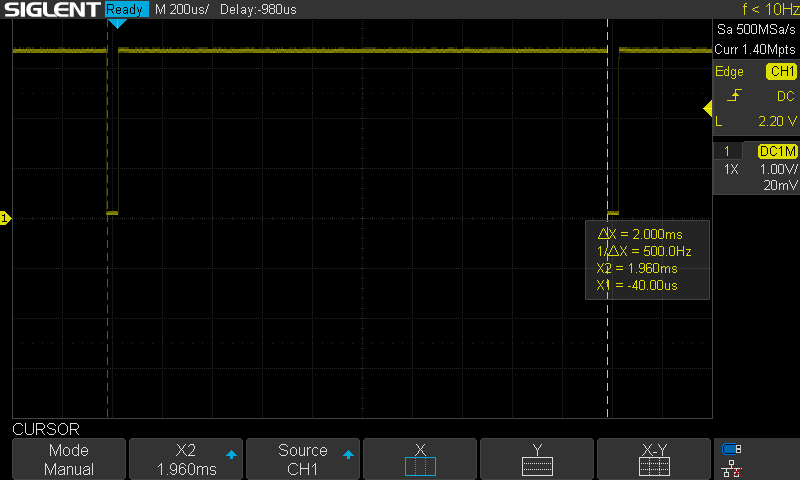
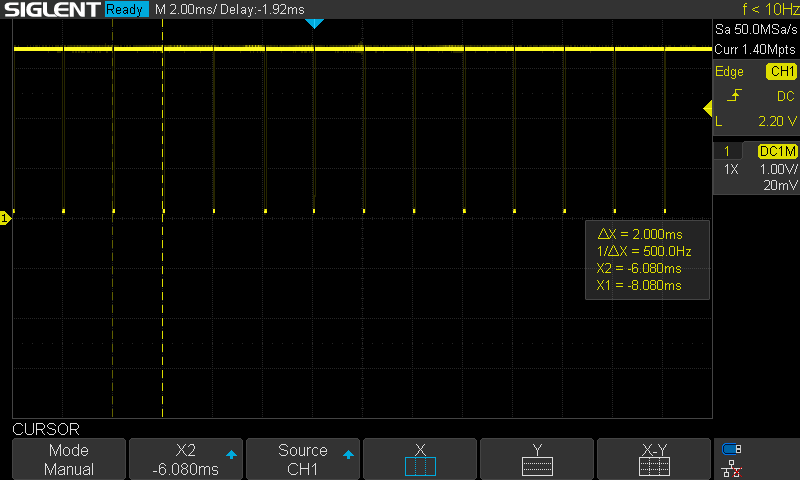
While I could simply run the controller within the ISR, I'd prefer to use that timer to consistently trigger a very high priority task to run the control. I implemented this using a task notification. While it did have a consistent period, I did see the occasional issue as shown at the center of the next image. Sometimes the computation time looked to be noticeably slower.
As currently configured, the timer task has higher priority than the control task, so likely that extra computation time is due to a preemption from the timer task. I added a 1ms delay to the primitive and telemetry timers to try to offset those from this timer. This seemed to resolve the issue (at least over short timeframes). In the long term, I need to make the control task higher priority than software timers.
VMC Optimizations
The pre-calculations of desired Bezier positions helps not only with position control, but also VMC. The VMC calculations need the current Cartesian position of the foot, and its desired position. This desired position can be and is pre-calculated, but the current position (forward kinematics) and virtual model still need to be calculated online. Looking at this again, I was able to add some optimization. The forward kinematics are as below:
And the Jacobian is defined as:
Therefore, there are some optimizations we can do while calculating the forward kinematics at the same time as the Jacobian.
void calculate_fk_and_jacobian(leg_ik_t * leg, pos_cartesian_t * pos, const pos_joint_space_t joint_angles, jacobian_t * j)
{
// Optimization, avoid calculating sin and cos functions twice
float ct = arm_cos_f32(joint_angles.thigh_angle_rad);
float st = arm_sin_f32(joint_angles.thigh_angle_rad);
float ctk = arm_cos_f32(joint_angles.thigh_angle_rad + joint_angles.knee_angle_rad);
float stk = arm_sin_f32(joint_angles.thigh_angle_rad + joint_angles.knee_angle_rad);
float temp_0 = leg->calf_length_m * ctk;
float temp_1 = leg->calf_length_m * stk;
pos->x = leg->thigh_length_m * ct + temp_0;
pos->y = leg->thigh_length_m * st + temp_1;
j->j_01 = -temp_1;
j->j_00 = -pos->y; // Optimization
j->j_11 = temp_0;
j->j_10 = pos->x;
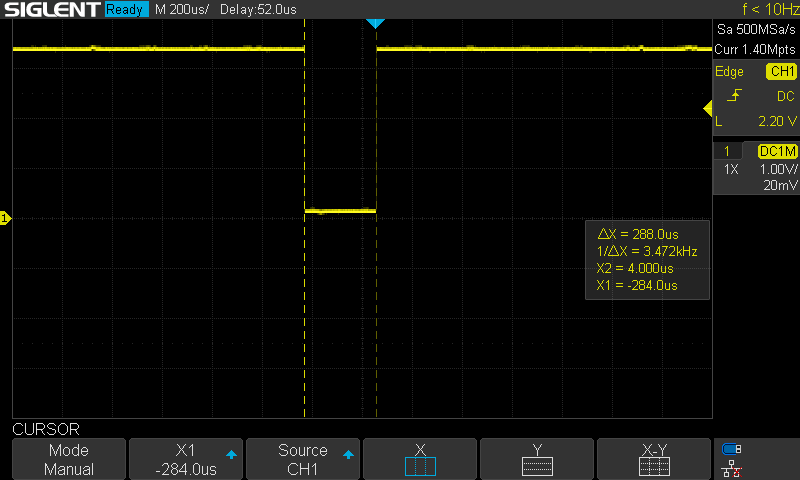
}Timing just that function is a bit disappointing though. It takes about 288us. This is a big constraint because I can't get around using Trig functions, and those are already optimized versions. Arm does provide fixed point versions, but it is not clear how I could implement what I need without needing some floating point conversions.
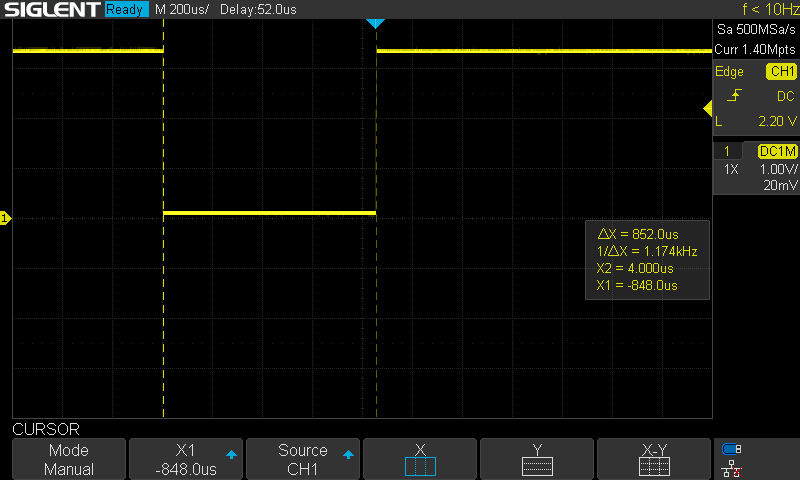
For the entire VMC primitive calculation, the situation is even worse. With damping (and speed estimation) brought back in, this takes about 852us per cycle. That said, that function is currently calculated at 100Hz, so we may be able to go a bit faster.
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.