-
Don't use a 555: Linear Resistance, Exponential Voltage
09/28/2021 at 14:33 • 0 commentsThe joke on Hackaday is: why use a microprocessor when you can use a 555? I'm proud to announce there are times when even a 555 is too much!
Musical notes increase in frequency exponentially. Every octave is a doubling of frequency. But the keyboard increases resistance linearly for each key pressed, and the VCO oscillator outputs a frequency that's linearly proportional to an input voltage. For example, It's easy to design a system that will output 10, then 20, then 30, then 40 Hz. It's a lot trickier to design a system that outputs 10, 20, 40, 80 Hz.
Most synthesizers use the exponential gain of BJT transistors to turn a linear voltage into an exponential voltage. But this requires matched resistors, thermal compensation, and circuit by circuit tuning. There are many things that have to accounted for, or else the notes will sound too close or too far apart.
Other cheap synthesizer keyboards use 555 timers and rely on the exponential discharge of an resistor and capacitor to get an exponential output. But 555 timers cost much more than an op amp, and it's hard to find ones that run at low voltage. So, I found a way to combine two op amps and a few resistors in such a way that a linear increase in resistance from the keyboard turns into an almost exponential voltage that the oscillator can use. Technically the response is polynomial not exponential, but the polynomial is within a fraction of a percent of a true exponential.
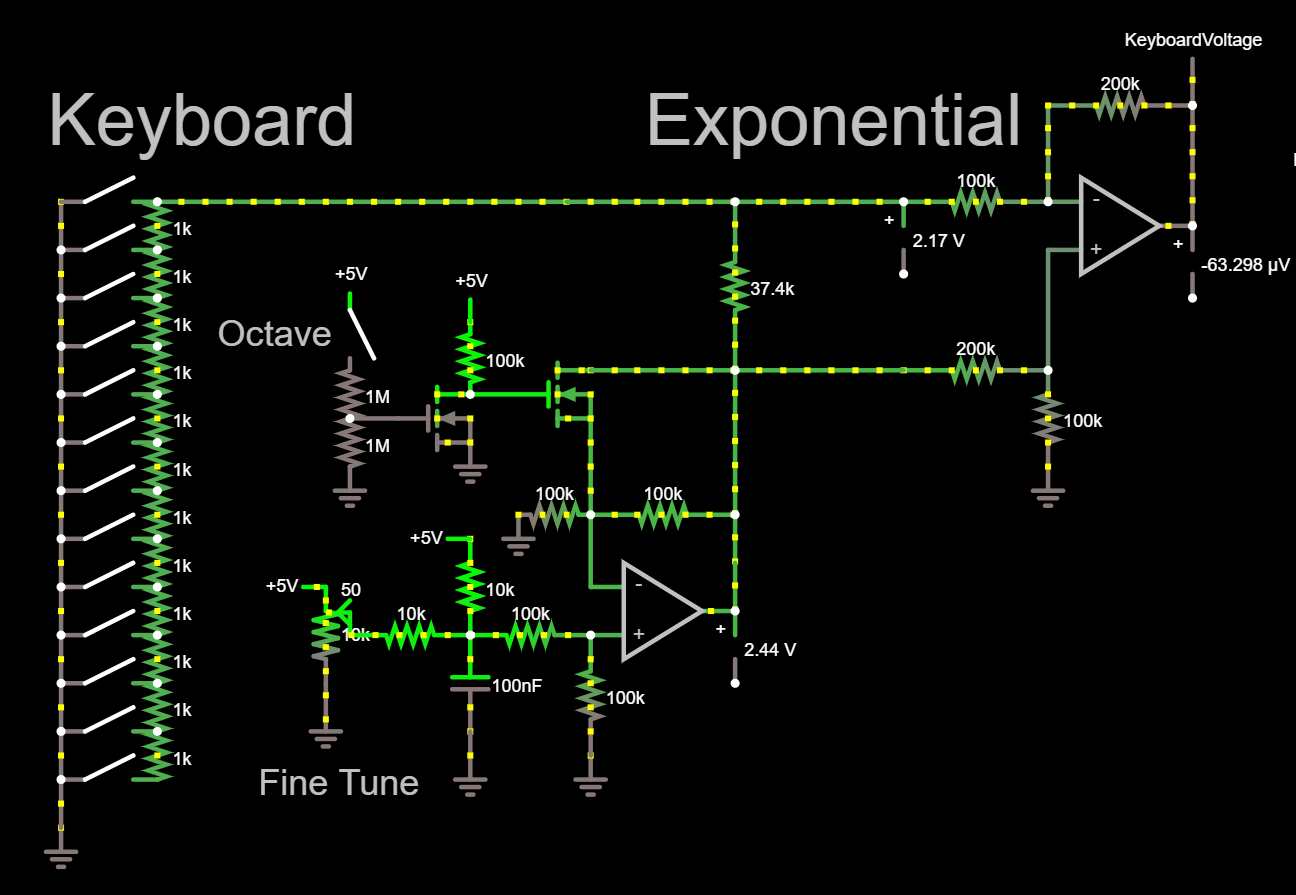
Keyboard: As discussed in a previous log, the keyboard is a series of transistors to ground, simulated here as a switch. Depending on which key is pressed, the keyboard will connect a different amount of resistance to ground. Each 1K ohm increment is one semitone (up one black or white key), with less resistance corresponding to higher pitch. If multiple keys are pressed, the highest pitch key will dominate, as all the lower keys will be shorted out.
Fine Tune: A potentiometer can adjust the voltage going into the op amp near where it says "Fine Tune". This voltage is used to shift the pitch of the whole keyboard.
Octave: The output of the fine tuning opamp can be either buffered with a gain of x1, or doubled. When the octave switch is unpressed, the op amp is configured as a unity gain buffer. But if the octave switch is closed, the op amp acts as a non inverting amplifier with a gain of 2. With one button, we can double the tuning pitch, which doubles the output frequency, giving us an octave.
Exponential: Now for the real math! The op amp that creates the exponential voltage for a linear change in resistance has no components that act exponential. How can this be? Consider the node between the keyboard and the exponential opamp. This node sees: 1) A resistor to ground that is a multiple of 1K, from the Keyboard. 2) A 37.4K ohm resistor to the tuner voltage. 3) a 100K ohm resistance to the virtual node of the exponential op amp. Because of the way the noninverting side of this opamp is set up, the virtual node will always be 1/3 the voltage of tuner voltage.
Finally, the op amp will double the voltage at this node, with reference to 1/3 the tuner voltage.
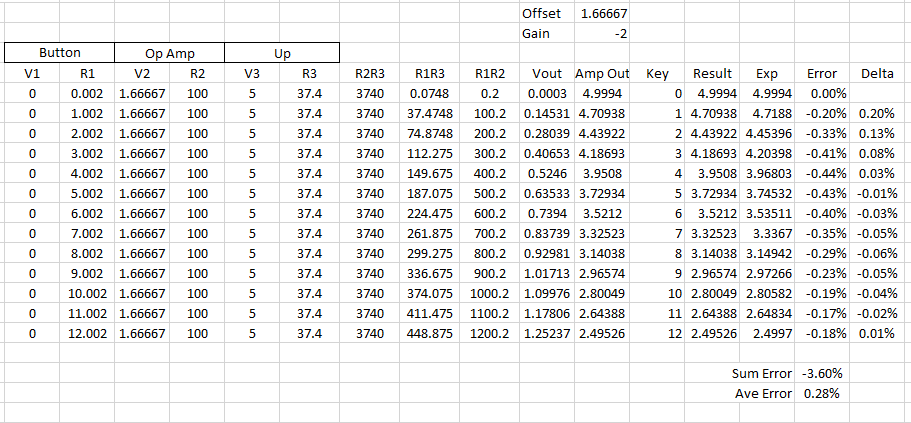
It's a ton of math! But also something any third level EE student can figure out. So if you've read this far, I encourage you to grind through the math to see what results you get. Here's what I got, from excel:
Each row shows the output voltage from a different key pressed, and compares it to an ideal exponential output. On average, the output voltage will be off by a fraction of a percent. This is less than the error we would get from the tolerance in our resistors. Anything within a percent or so is great for a toy synthesizer.
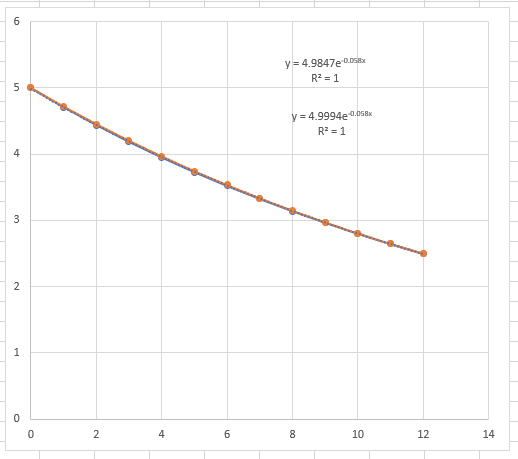
As you can see from the graph comparing the calculated opamp output to an exponential output... They are the same line. By carefully selecting components, We've found a polynomial equation that pretty much perfectly lines up with our desired exponential output. We're using standard easy to source parts (a 37.4K ohm resistor is a bit rarer but still a standard value). And best of all, we don't have to worry about thermal compensation or part to part variation, like we would if we were using BJT transistors.
And this output is scaled relative to the reference voltage. If you change the octave or the tuner voltage, the exponential curve will be scaled. But the proportional rate that voltage changes per key will stay the same, and the note spacing will stay the same.
Connect this exponential output to a linear VCO tuned to play notes in the range of musical notes, and you have yourself a simple keyboard! But it is only simple because of all the design and calculations we put into it.
-
Images for last post, oops!
09/28/2021 at 13:48 • 0 commentsOops, the images didn't save in my last post and I can't seem to edit or delete it it. Sorry about that, it looks like I need to upload the images and can't just paste it into the text box! So here are the images:
"Here is part of the schematic for the first version of the touch pad..."
"The human body model of ESD models an ESD event as having 100pF of capacitance..."
-
Resistive Touch Pads for Keys
09/28/2021 at 13:43 • 0 commentsTo keep the MicroSynth simple and low profile, I experimented with using touch pads instead of mechanical switches. Other circuits can use capacitive sensors connected to microprocessors, but because this circuit is all analog and designed to be as simple as possible, I made a resistive, not capacitive, touch pad.
![]()
Here's what the first version of the touch pad looks like. Pressing a touch pad key with your fingertip allows a tiny amount of current to flow across the touch pad. This current is just enough to turn on a transistor. It's like a membrane button you'd see if you took apart a calculator, but your finger is the button pad. Where the black keys would be, you can see the individual transistors, with a capacitor and two resistors below.
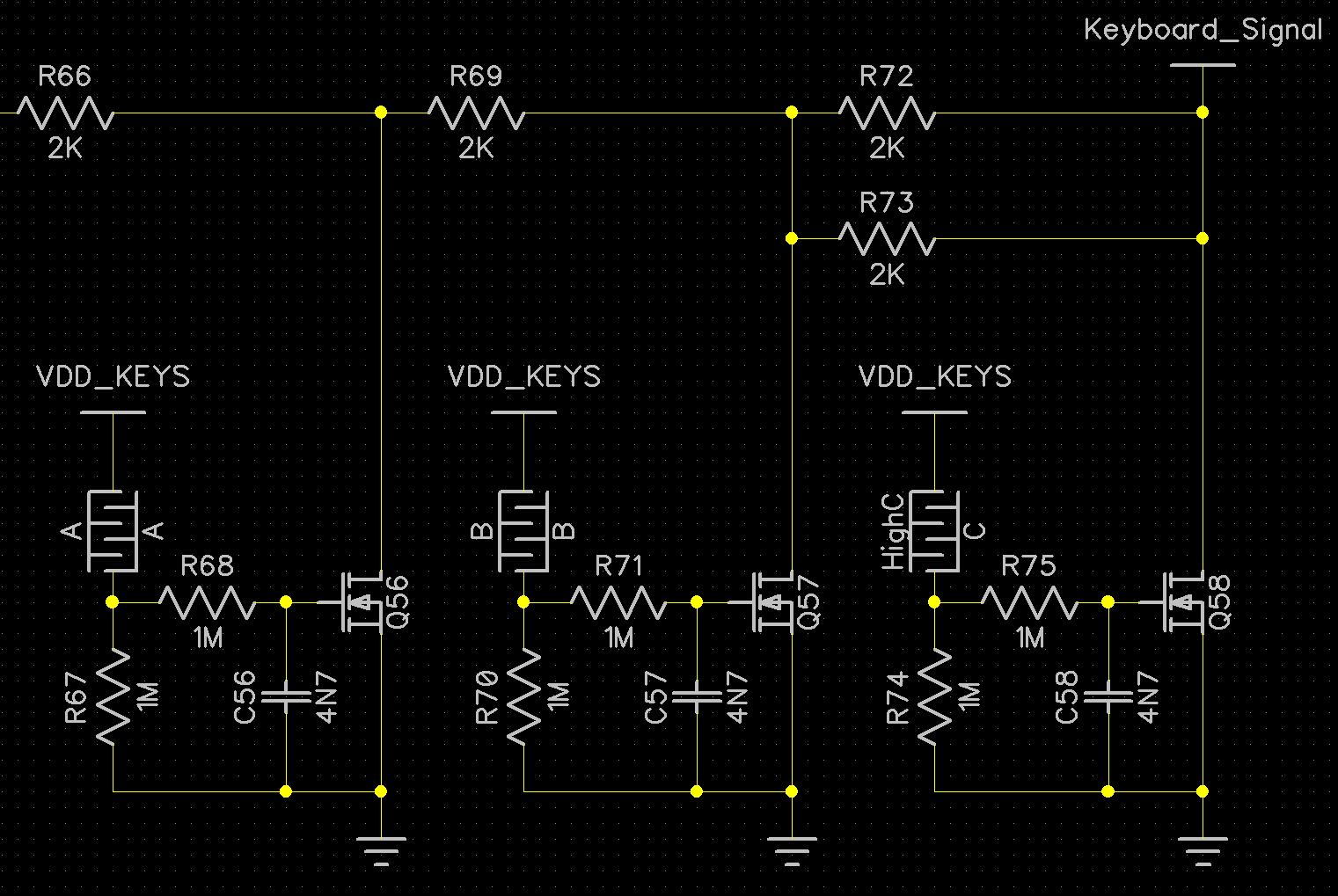
Here is part of the schematic for the first version of the touch pad. When a NFET is turned on, it will connect the "Keyboard_Signal" net to ground with a certain amount of resistance. Q58 is a direct connection to ground, Q57 is 1K to ground, Q56 is 3K ohms to ground ect. Each 1K increment is equal to one musical semitone, but because I skip the black keys, it sometimes jumps by 2K instead of 1K ohms.
Now onto how these transistors actually turn on. The interlocking squiggle patterns A, B, C, represent the touch pads for keys A, B and C. When they are unpressed, they are just an open switch. But, when your finger presses onto them, it creates a resistance across two sides of the touch pad. Your finger turns the touchpad into a resistor of between maybe half a megaohm to a couple megaohm, depending on the person and how hard they press.
So, when the key is unpressed, it is pulled down by a large resistor (R74). When it is pressed, it is pulled up above the threshold voltage of the transistor, causing it to turn on and send a signal out to the "Keyboard_Signal" net.
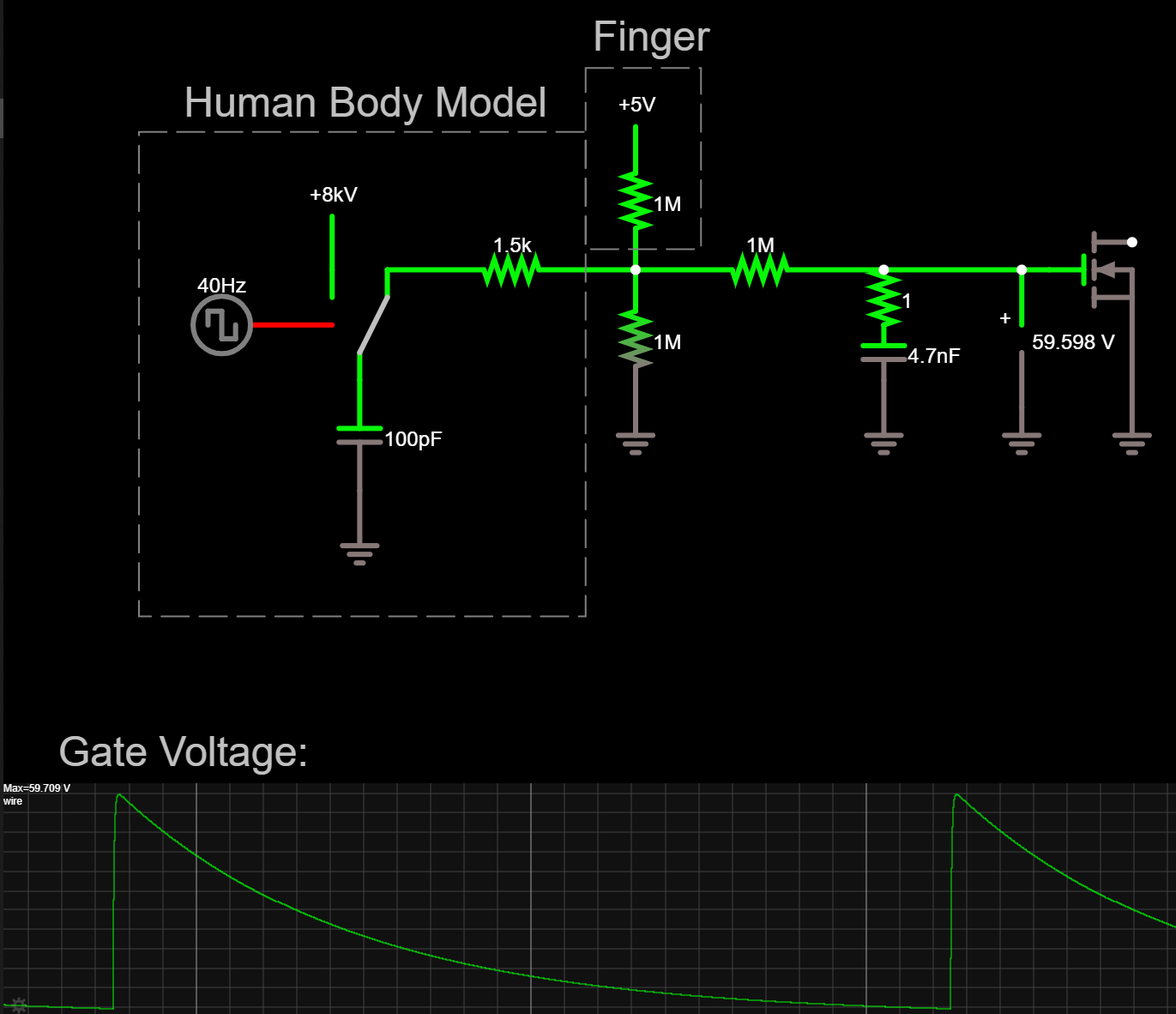
But what's the purpose of the resistor and capacitor in front of the FET's gate? A FET transistor has very high impedance, and the signal will not be affected much by an extra 1M ohm. But what could effect the FET is electrostatic discharge.
The human body model of ESD models an ESD event as having 100pF of capacitance. The more capacitance, the more charge stored up. And capacitance is how much charge can be stored per volt (C=q/V). So, if we move 10 volts of charge from a 100pF capacitor to a 1000pF capacitor, the new larger capacitor will only have 1 volt charged up.
In the MicroSynth, I use a 4.7nF cap, a cap about 50 times larger than the human body model. So we'd expect a 8000 volt ESD zap to turn into 160V once it reaches the cap. The 1 M ohm resistor before the gate helps slow down the rate of charge and helps the ESD discharge through the pulldown resistor and the fingertip. Based on the simulations above, only 60V reaches the gate of the FET. This is still enough to cause harm, but luckily most discrete FETs have a built in ESD diode to protect against some amount of ESD. With all these parts in place, we don't have to worry about static electricity burning a hole in our transistor gate.
There's still things to improve with this circuit however. I apparently have relatively sweaty fingertips, so my resistance is lower on a touch pad. But my friends have drier hands, and need to press down harder to fully turn a key on. I'll be experimenting with different ways to increase the sensitivity of these keys. I can chose a power FET that has a lower turn on voltage, I could buffer the input with a BJT transistor to increase the overall gain, I could even pull the gate to just below its threshold level instead of all the way to ground.
But, this circuit definitely works. And it is so much cheaper and more fun than a regular old mechanical switch
MicroSynth: Part Biz Card, Part Synth, All Analog
A Tiny, Low Cost, Super Simple Synth for Fun and Learning
 David Levi
David Levi