[En svensk version finns i slutet av inlägget]

Background 

Two years ago I bought a boat with the hope that someday be able to electrify it. It is a displacement boat of a type called snipa or snäcka which typically has low drag at low speeds. For that reason I chose this boat type, the boat is a bit bigger than what I planned for, and I think that is the theme for most of this build. It is a Sandvik 25 and currently, it has a Volvo Penta MD3B as the engine. 

It has a displacement of 2400kg according to the old datasheet. But it is probably more with the equipment that has been added over the years. Before starting the conversion we exchanged the rubber gasket on all windows to keep the rain on the outside of the boat since that was a bit of a problem before. Because it does feel quite important to keep the water outside of the boat before installing a high-voltage battery in it. We also repainted the bottom as it was for lakes and not for the sea.

Initial testing

At the end of the first summer with the boat, we went out and made a small test logging the rpm of the motor, GPS speed as well as speed through water (not used). During the test we drove back and forth with one rpm setting before increasing it to 100rpm, writing down the speed after it had stabilized after each turn. After a total of 30 turns, we were done with the test, and the average results of the data look like this: 

My idea is to use this data to estimate the maximum power used to propel the boat at different speeds. I say maximum because it assumes that the engine can produce the power it could when it is brand new, which it most probably can not do. As well as there are other losses on the way to the propeller, which also should make the estimated power a bit higher.

A simple generic equation for static thrust can be found in this paper, which describes the relationship between the rpm and thrust using this equation: 

Where T_s is the static thrust produced (in newtons), K_t is the thrust coefficient, ρ is the air density (in kg/m^3), ω is the propeller speed (in rad/s), and D is the diameter of the propeller (in m). I have removed some constants and changed units since K_t will just be scaled accordingly.

It only holds for stationary propellers, so let's hope that the propeller moves somewhat slowly enough through the water. And that there is not too much growth on it making the equation break even more. But this should only make the estimated power used to propel the boat higher, resulting in a further range after the actual conversation.

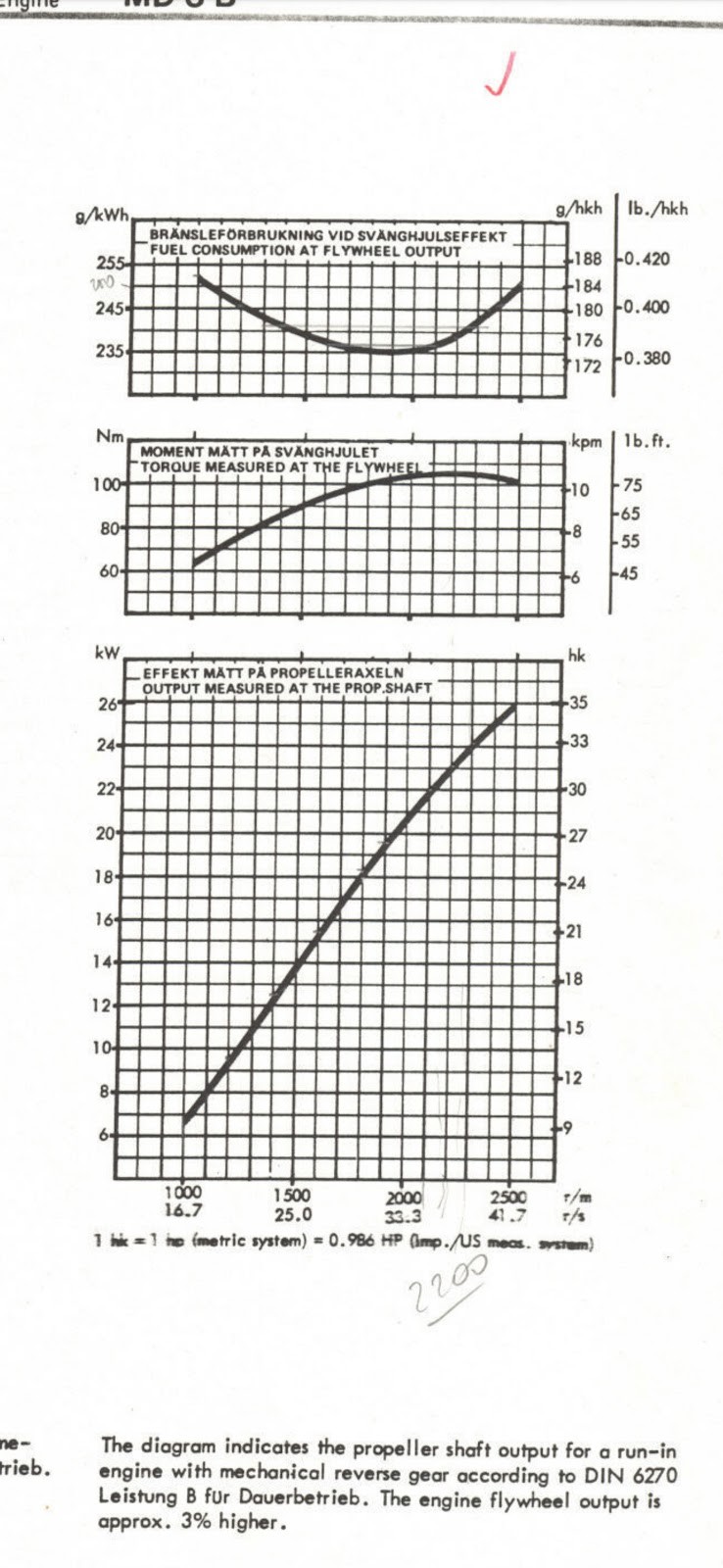
First, we find the power produced by the engine at the specific rpm. In the datasheet for the engine, such a point can be found for full throttle.

Then the rpm of the engine needs to be converted to the propeller speed, which has a reduction of 1.91 and then I also convert it to rad/s.

Since the speed of the boat, Vmax (in m/s), and power produced by the vessel, Pmax (in kW), is known at the max rotational speed of the propeller (in rad/s). We can solve for the thrust produced by the propeller: 

Fmax can then be plugged into our thrust equation, where it is called T_s, which we then can solve for the constant. This constant replaces all the other constants since they can be multiplied together. Resulting in this equation:

This new constant, K, can now be used to calculate the thrust produced at a certain rpm of the vessel, and since the velocity is already known the power used can be estimated. 

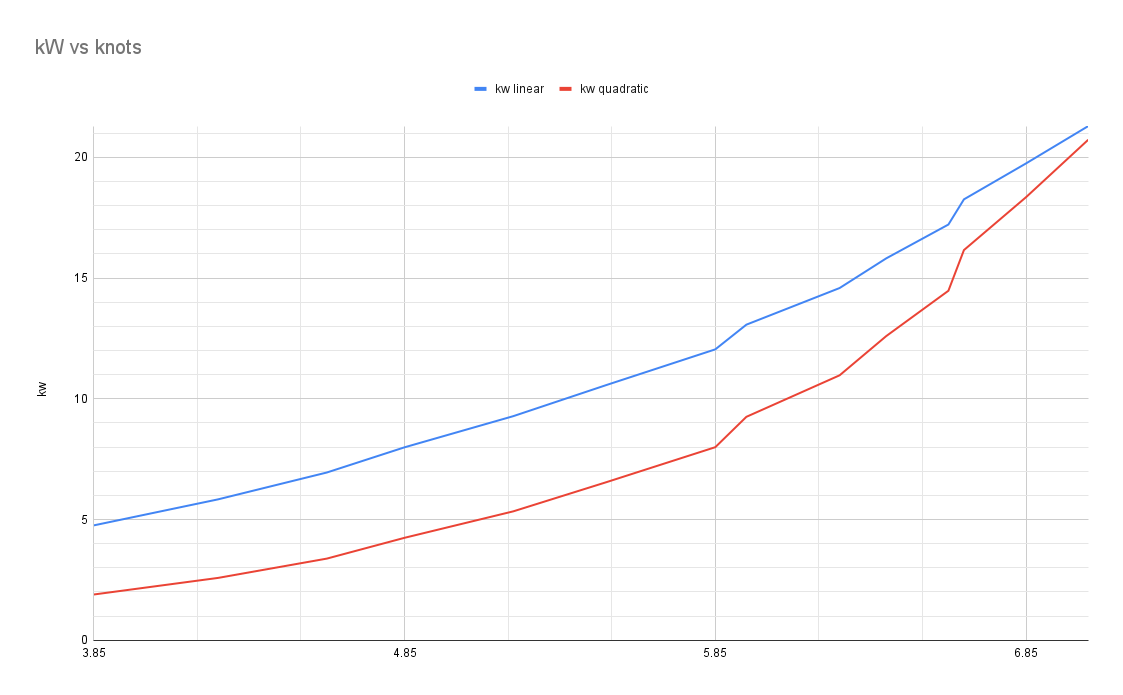
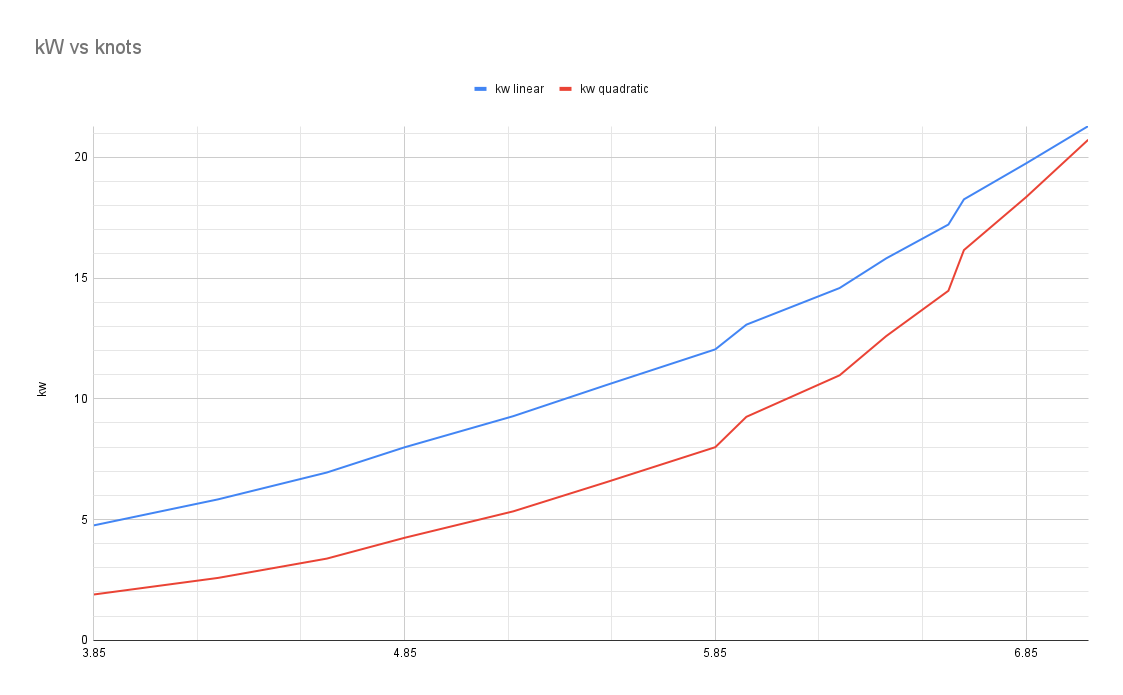
I did also do the calculations with a linear version of the formula (removing the square), to make a worse estimate at lower speeds. The electric motor will also have some inefficiency which will mean that more power will be pulled from the battery than is required to propel it forward. The results from both can be seen below:

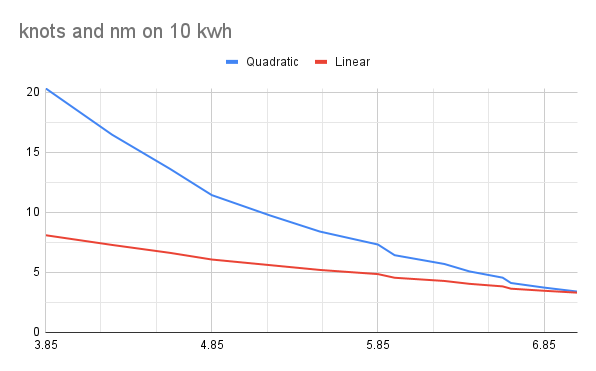
I have also done calculations on the range with a 10 kWh battery, which can be seen here (just divided the kilowatt-hours by kilowatt at a certain speed and multiplied it by the speed in knots): 

At the end of the post, the raw data can be found.

Svenska - Bakgrund 

För två år sedan köpte jag en båt med förhoppningen att någon dag kunna elektrifiera den. Det är en snipa, vilken vanligtvis har lågt motstånd vid låga hastigheter. Vilket är varför jag har valt den här båttypen, båten är lite större än vad jag planerade för, och jag tror att det är temat för det mesta av denna konverteringen. Det är en Sandvik 25 och för närvarande har den en Volvo Penta MD3B som motor. 

Den har en deplacement på 2400 kg enligt det gamla databladet. Men det är förmodligen mer med utrustningen som har lagts till under åren. Innan vi började konverteringen bytte vi ut gummilisten på alla fönster för att hålla regnet utanför båten eftersom det var lite av ett problem innan. Det känns ganska viktigt att hålla vattnet utanför båten innan man installerar ett högspänningsbatteri i den. Vi målade också om botten eftersom den var avsedd för Vänern och inte för västkusten.

Inledande testning

I slutet av den första sommaren med båten åkte vi ut och gjorde ett litet test där vi loggade motorns varvtal, GPS-hastighet samt hastighet genom vatten (används ej). Under testet körde vi fram och tillbaka vid ett visst varvtal innan vi ökade den med 100 RPM. Vid varje vända så skrev ner hastigheten efter att den hade stabiliserat sig. Efter totalt 30 rundor var vi klara med testet, och resultaten av datan ser ut så här: 

Iden jag har är att använda datan för att uppskatta den maximala effekt som används för att driva båten vid olika hastigheter. Jag tror att det är max eftersom min ide antar att motorn kan producera den effekt den kunde när den är helt ny, vilket den troligen inte kan göra. Iden antar även att all effekt som motorn producerar driver båten frammåt, detta är inte heller sant och de förlusterna som finns på vägen fram till propellern kommer också innebära att det beräknade kommer vara högre än verkligen.

En enkel ekvation för att beskriva förhållandet mellan varvtal och statisk dragkraft från en propeller finns i den här rapporten, och innehåller följande ekvation: 

Där T_s är den producerade kraften (i newton), K_t är dragkraftkoefficienten, ρ är luftens densitet (i kg/m^3), ω är propellerns hastighet (i rad/s) och D är propellerns diameter (i m). Jag har bytt enheter och plockat bort konstanter, men det kommer endast skala K_t.

Ekvationen gäller dock bara för stationära propellrar i öppet vatten, så jag får hoppas att min propeller rör sig tillräckligt långsamt och att det inte finns för mycket påväxt på den som gör att ekvationen fungerar ännu sämre. Men om det är fel så bör det bara göra den uppskattade effekten som används av motorn högre, vilket resulterar i ett längre sträcka som båten kan köra efter den faktiska konverteringen.

Först hittar vi den effekt som produceras av motorn vid det specifika varvtalet. I databladet för motorn kan man hitta en sån punkt vid full gas.

Sedan behöver motorns varvtal konverteras till propellerhastighet, bakslaget har en reduktion på 1,91 och sedan konverterar jag det också till rad/s.

Eftersom båtens hastighet, Vmax (i m/s), och effekten som produceras av motorn, Pmax (i kW), är känd vid den maximala rotationshastigheten för propellern (i rad/s). Kan vi lösa för den dragkraft som produceras av propellern: 

Fmax kan sedan sättas in i vår dragkraftsekvation, som vi sedan kan lösa för konstanten. Denna konstant ersätter alla andra konstanter eftersom de kan multipliceras tillsammans. Vilket resulterar i denna ekvation:

Denna nya konstant, K, kan nu användas för att beräkna den dragkraft som produceras vid ett visst varvtal på båten, och eftersom hastigheten redan är känd kan den användas för att uppskatta den använda effekten. Detta kan ses nedan:

Jag gjorde också samma beräkningar med en linjär version av ekvationen (tog bort kvaderaten) för att få ett ännu värre estimat. Den elektriska motorn kommer också att ha viss ineffektivitet vilket innebär att mer effekt kommer att dras från batteriet. Resultaten kan ni se här:

Jag har också gjort beräkningar av räckvidden med ett 10 kWh-batteri, vilket kan ses här (jag delade bara kilowattimmar med kilowatt vid en viss hastighet och multiplicerade med hastigheten i knop): 

Här under finns datan som jag har samlat ihop.

Data

Below you can find the data that we have collected and the calculations that I have done:

Nedan finns datan vi har samplat ihop och beräkningarna jag har gjort:

Quadratic:

knots	RPM (propeller)	force [n]	speed [m/s]	power [kw]	rad/s	Torque [nm]
3.85	471.2041885	956.7730036	1.980452675	1.894843654	49.34438723	38.40038879
4.25	523.5602094	1181.201239	2.186213992	2.582358676	54.82709692	47.10004397
4.6	575.9162304	1429.253499	2.366255144	3.381978445	60.30980661	56.07675823
4.85	628.2722513	1700.929784	2.494855967	4.243574822	65.79251631	64.49935433
5.2	680.6282723	1996.230094	2.674897119	5.339710128	71.275226	74.91677582
5.5	732.9842932	2315.154428	2.829218107	6.550076829	76.75793569	85.33419731
5.85	785.3403141	2657.702788	3.009259259	7.997716722	82.24064538	97.24773785
5.95	837.6963351	3023.875172	3.060699588	9.255173494	87.72335507	105.5040985
6.25	890.052356	3413.671581	3.215020576	10.97502437	93.20606477	117.7501099
6.4	942.408377	3827.092014	3.29218107	12.59947988	98.68877446	127.6688251
6.6	994.7643979	4264.136473	3.395061728	14.47700654	104.1714842	138.9728356
6.65	1047.120419	4724.804956	3.420781893	16.16252724	109.6541938	147.3954317
6.85	1099.47644	5209.097464	3.523662551	18.35510166	115.1369035	159.4197959
7.05	1151.832461	5717.013997	3.62654321	20.73299829	120.6196132	171.8874546

Linear:

knots	RPM (propeller)	force [n]	speed [m/s]	power [kw]	rad/s	Torque [nm]
3.85	471.2041885	2402.56332	1.980452675	4.758162954	49.34438723	96.42764296
4.25	523.5602094	2669.5148	2.186213992	5.836130607	54.82709692	106.4460994
4.6	575.9162304	2936.46628	2.366255144	6.948428441	60.30980661	115.2122487
4.85	628.2722513	3203.41776	2.494855967	7.992065914	65.79251631	121.473784
5.2	680.6282723	3470.36924	2.674897119	9.282880684	71.275226	130.2399334
5.5	732.9842932	3737.32072	2.829218107	10.57369545	76.75793569	137.7537757
5.85	785.3403141	4004.2722	3.009259259	12.04989319	82.24064538	146.519925
5.95	837.6963351	4271.22368	3.060699588	13.07293256	87.72335507	149.0245391
6.25	890.052356	4538.17516	3.215020576	14.59032652	93.20606477	156.5383814
6.4	942.408377	4805.12664	3.29218107	15.81934696	98.68877446	160.2953026
6.6	994.7643979	5072.07812	3.395061728	17.22001831	104.1714842	165.3045308
6.65	1047.120419	5339.0296	3.420781893	18.26365578	109.6541938	166.5568378
6.85	1099.47644	5605.98108	3.523662551	19.7535856	115.1369035	171.566066
7.05	1151.832461	5872.93256	3.62654321	21.2984437	120.6196132	176.5752943

Time/Distance:

knots	time on 10kwh Quadratic	nm on 10 kwh Quadratic	time on 10kwh Linear	nm on 10 kwh Linear
3.85	5.27748027	20.31829904	2.101651435	8.091358025
4.25	3.872428758	16.45782222	1.713464052	7.282222222
4.6	2.956849124	13.60150597	1.439174352	6.62020202
4.85	2.356503755	11.42904321	1.251240932	6.068518519
5.2	1.872760835	9.738356345	1.077251808	5.601709402
5.5	1.52669965	8.396848073	0.9457431457	5.201587302
5.85	1.250356864	7.314587654	0.8298828743	4.854814815
5.95	1.080476774	6.428836806	0.7649393091	4.551388889
6.25	0.9111597078	5.694748174	0.6853856209	4.283660131
6.4	0.7936835562	5.07957476	0.6321373457	4.045679012
6.6	0.690750534	4.558953524	0.5807194755	3.832748538
6.65	0.6187151211	4.114455556	0.5475355054	3.641111111
6.85	0.5448076608	3.731932477	0.506237207	3.467724868
7.05	0.4823229067	3.400376492	0.4695178738	3.31010101