Gamma ray attenuation follows the law
- I is the intensity of beam after attenuator
- I0 is the intensity of beam before attenuator
- μ is the attenuation coefficient
- x is the attenuator thickness
The attenuation coefficient depends both on the material of the attenuator as well as on the gamma ray energy. This is why serious gamma ray shielding is made of lead, and high energy gamma rays are harder to stop.
Setup

An Am-241 source (red X in the picture) gives off gamma rays towards the detector. A stack of aluminum plates acts as the shielding that is being measured
The detector is the gamma spectroscopy module I've been recently working on. It can detect the 59.5 keV gamma rays from Am-241 and is used here to count how many such events are being measured for different attenuator thicknesses.
The attenuator is a stack of 2mm aluminum plates. I used up to 10 plates, for a total of 2cm of shielding.
While not strictly necessary for this experiment, I placed the Am-241 source behind a rudimentary collimator made out of a stack of steel washers.

Am-241 collimator made from a stack of steel washers held together with electrical tape
Normally the attenuator would help to reduce buildup in the detector, that is photons that scattered off of something else and ended up measured afterwards. But since I'm counting just the events in the full energy peak of 59.5 keV this is not that big of an issue.
Measurements
This measurement is quite sensitive to the background which one could try to reduce as much as possible by measuring everything in a lead castle. Otherwise, one can do background subtraction carefully. I cannot just take a measurement without the source and subtract that from all subsequent measurements, because as I add shielding in front of the detector that will also reduce the background coming from that side -- background events come from everywhere around the detector.
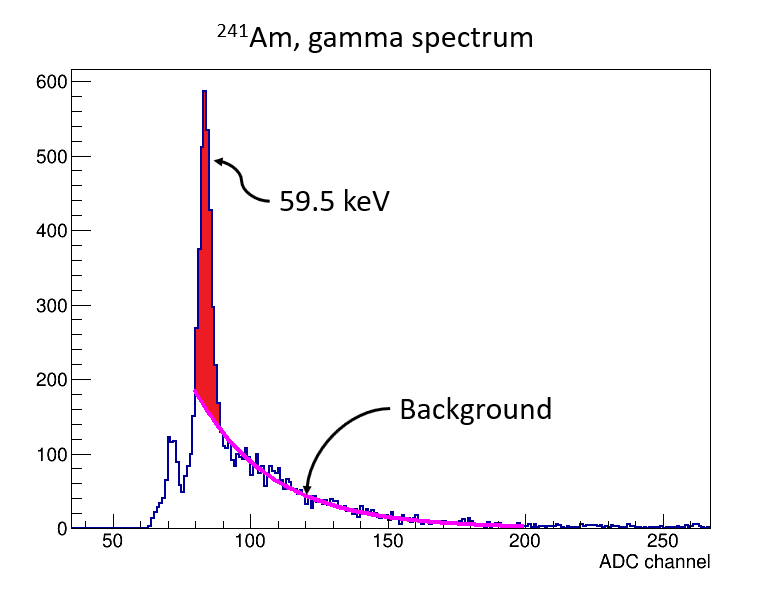
Am-241 spectrum with 20mm aluminum shielding. The effective number of counts for this measurement is just the red section, that which is above the estimated purple background
To estimate the background I fit the spectrum with an exponential decay between ADC channel 100 and 200, above the 59.5 keV energy peak. Then I extrapolate this background under the peak and subtract the background integral from the peak integral.
Taking one 5 minute run for each attenuator thickness and computing the background subtracted counts in the 59.5 keV peak yields the following results:
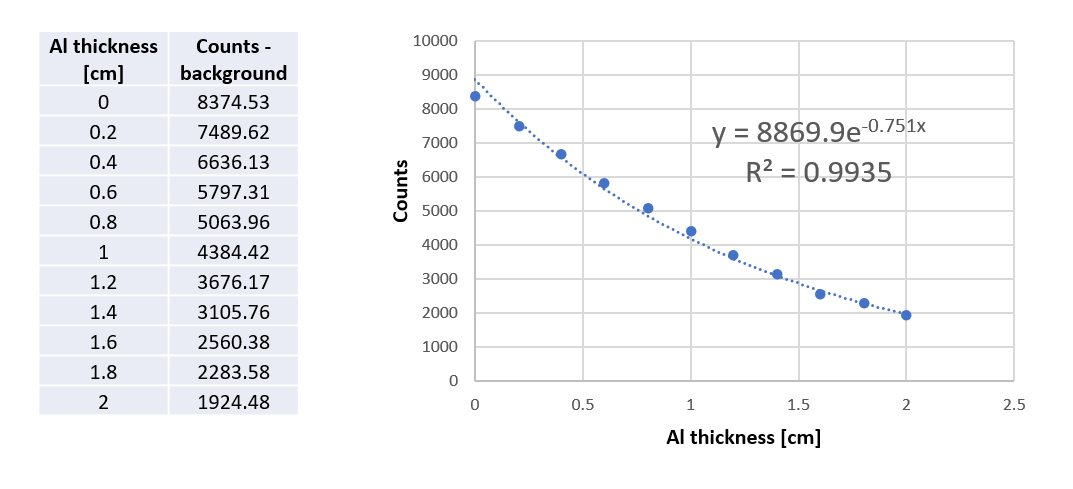
Resulting data set and fit with an exponential to get the parameters for the I = I0*exp(-mu*x) law
The attenuation law is confirmed, as the plot can easily be fitted with an exponential function with a very good R^2. The value obtained for the attenuation coefficient μ is 0.751 cm^-1
Conclusions
The resulting value of μ of 0.751 cm^-1 is in very good agreement with the literature value. the NIST attenuation coefficients for aluminum quote a value of μ/ρ of 0.2778 cm^2/g at 60 keV. Multiplying that by the density of aluminum (ρ = 2.699 g/cm^3) gives μ = 0.75 cm^-1
 mihai.cuciuc
mihai.cuciuc

 MOST
MOST

 Robert Hart
Robert Hart