In Part 1 of this soon-to-be epic series of columns, we discussed the fact that we are going to explore electronics and microcontrollers starting at the most fundamental level. We are also going to learn some useful skills, like how to not burn ourselves with a soldering iron (it took me years to perfect this one).
Last, but certainly not least, we introduced the Cool Beans and their Cool Beans Blog. In this column, we are going to introduce the concepts of voltage (V), current (I), and resistance (R). Just to help out, as seenin the image below, the Cool Beans have donned corresponding T-shirts in order to take place in a demonstration later (I apologize in advance for resistance, who is a bit of a pain at the best of times, and who had enjoyed a tad too much coffee and was grooving to his own internal soundtrack at the time the artist captured this likeness).
 The Cool Beans sporting their voltage (V), current (I), and resistance (R) T-shirts (Image source: Max Maxfield)
The Cool Beans sporting their voltage (V), current (I), and resistance (R) T-shirts (Image source: Max Maxfield)
Whenever we build an electrical or electronic circuit (we’ll discuss the difference in a later column), we cannot help but run into voltage, current, and resistance. One way to visualize these little scamps is to use an analogy based on a 2-liter plastic fizzy drink bottle. This is a great experiment for you to replicate at home, especially if you are teaching this stuff to someone else.
First, drink or discard the original contents, wash the bottle out, remove any external labels, and use a permanent marker to draw a series of horizontal lines up the side as illustrated below. Mark the lowest graduation 0 and count from there. I used 18 graduations in my diagram, but you can use as many as you want.
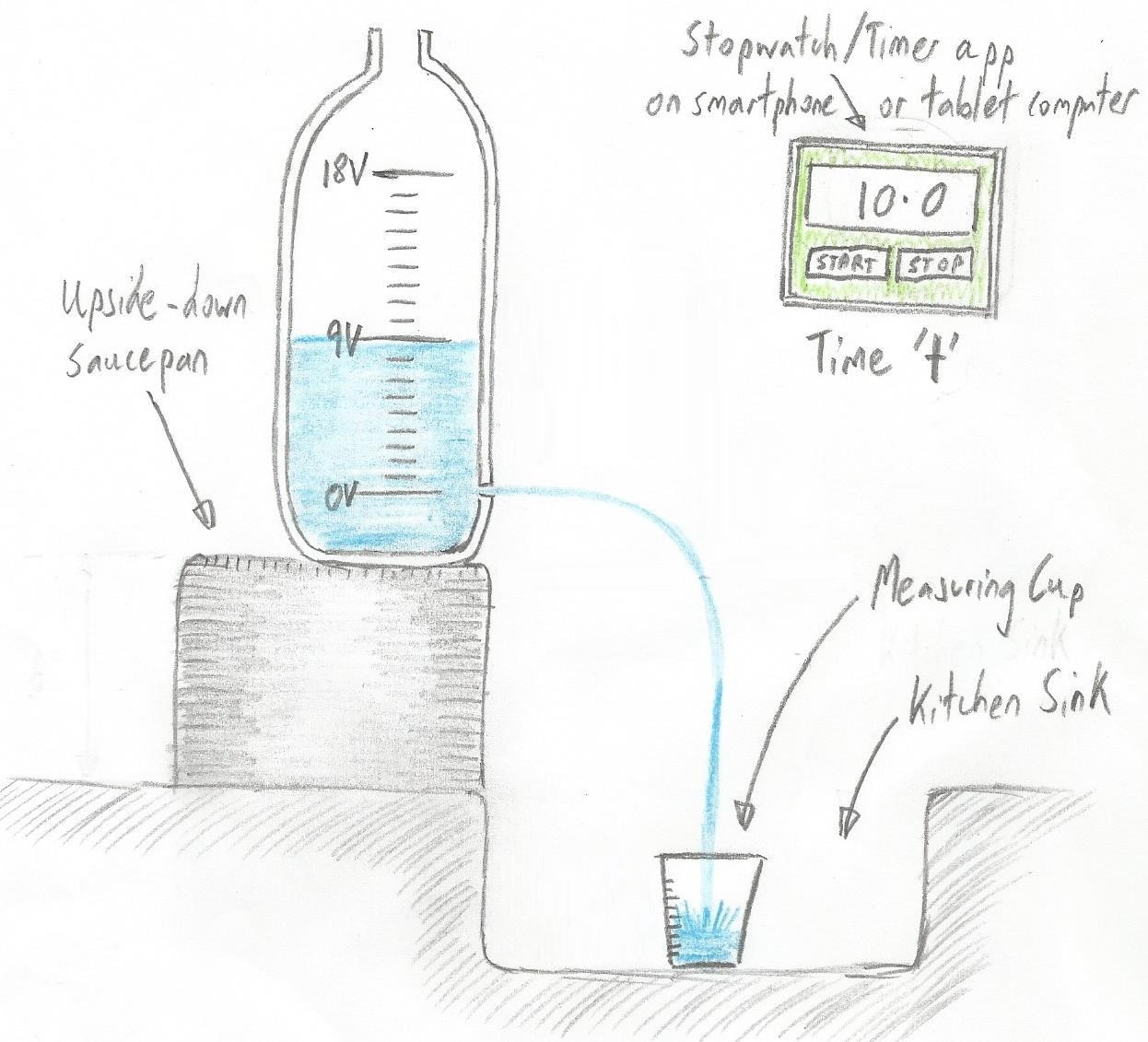 Representing voltage, current, and resistance with a water analogy (Image source: Max Maxfield)
Representing voltage, current, and resistance with a water analogy (Image source: Max Maxfield)
We are going to use the height of the water in the bottle to represent voltage (V) in an electrical system. Fill your bottle halfway (the 9 V mark on my diagram), stand it on something like an upturned saucepan next to your kitchen sink, and put a small measuring cup in the sink. Carefully punch a hole (say 2 mm diameter) into the bottle at the 0 V mark and record how long it takes to fill the measuring cup to some pre-defined level you’ve selected (say 1/4 of a cup). If you don’t have a timer, just counting “one Mississippi, two Mississippi, three Mississippi...” will be close enough for our purposes here.
The hole resists the flow of the water. In our analogy, we’re using the hole to represent the resistance (R) in an electrical system. In the same way that the hole resists or limits the amount of water that can pass through the hole, so does resistance in an electrical circuit resist or limit the flow of electricity.
Finally, let’s turn our attention to current (I). In an electrical circuit, we might think of current as being the amount or quantity of electricity flowing through the circuit. The equivalent in our water analogy is the amount of water flowing through the hole at any particular point in time.
 We can think of voltage (V) as pushing current (I) while resistance (R) does its best to impede things (Image source: Max Maxfield)
We can think of voltage (V) as pushing current (I) while resistance (R) does its best to impede things (Image source: Max Maxfield)
Let’s return to our trusty Cool Beans (if you can’t trust a Cool Bean, who can you trust?). In the case of our water example, we might think of our voltage (V) bean as trying to push our current (I) bean through the hole, while our resistance (R) bean does its best to impede things.
The Relationship Between Voltage, Current, and Resistance
So, how can we determine the relationship between voltage, current, and resistance using our water analogy? Well, let’s begin by repeating our experiment, but this time let’s start with the bottle filled to the topmost mark (the 18 V mark on my diagram).
Remembering that this is a really rough-and-ready setup, we should find it takes about half the time to fill the measuring cup to the same level as before. That is, if we keep the diameter of the hole (the resistance) the same, then doubling the height of the water (the voltage) doubles the amount of water flowing through the hole (the current).
One way to think about this is that the greater the depth of water inside the bottle above the hole, the greater the pressure of the water inside the bottle on the other side of the hole. So, we can think of the depth of the water (voltage) as equivalent to the “pressure” that forces the water (current) through the hole (resistance).
Next, let’s increase the size of the hole. It used to be 2 mm in diameter. If we increase this to 3 mm in diameter, this will approximately double the hole’s cross-sectional area, thereby halving its resistance to the flow of water.
Now, let’s repeat our experiment starting with the bottle filled to the topmost mark (the 18 V mark on my diagram). We should find it takes about half the time to fill the measuring cup to the same level as before (that’s a quarter of the time it took using our original hole with the water starting at the halfway mark). That is, if we keep the height of the water (the voltage) the same, then doubling the cross-sectional area of the hole (which equates to halving its resistance) doubles the amount of water flowing through the hole (the current).
Based on the above, can you think of a simple equation that would tie all of this together? The German physicist Georg Simon Ohm (1789–1854) captured the equation that defines the relationship between voltage, current, and resistance in 1827, and we now call this relationship Ohm’s law. We’ll look at this in more detail in my next column, but first...
Introducing Electric Charge
There are two types of electric charge: positive and negative (commonly carried by protons and electrons respectively). Like charges repel each other and unlike charges attract each other. An object with an absence of net charge is referred to as neutral.
Purely for the purposes of these discussions, let’s assume that the volume of water in our 2-liter bottle equates to the amount of electric charge in an electrical system. Suppose our 2-liter bottle was acting in the role of a battery. If we start with a full bottle and let the water drain out, after some period of time the bottle will be empty; that is, our “battery” will be drained or discharged.
Suppose we wanted a bigger battery that lasted longer? Do you remember our experiment in which we had a 2 mm diameter hole in the bottom of our 2-liter bottle and we filled it to the 18 V mark? Well, how about if we took a bathtub with a 2 mm diameter hole in the bottom and we filled it with water to the same depth as the 18 V mark on our bottle. What do you think would happen?
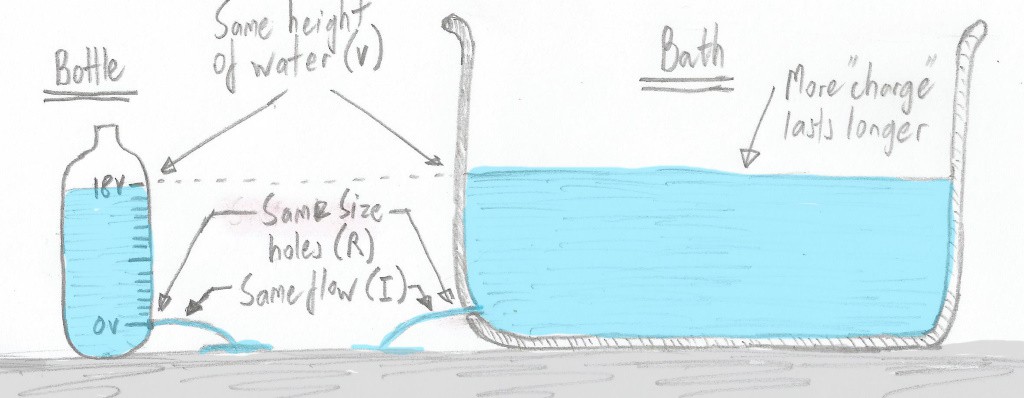 In the same way that the ‘height’ of the water equates to voltage (V) in our analogy, the ‘volume’ of water equates to charge (Image source: Max Maxfield)
In the same way that the ‘height’ of the water equates to voltage (V) in our analogy, the ‘volume’ of water equates to charge (Image source: Max Maxfield)
Remember that the amount of water passing through the hole at any particular time depends only on the height of the water (V) and the resistance (R) of the hole. The fact that we are now using a bathtub rather than a 2-liter bottle doesn’t really change anything -- the water will come out at the same rate -- the only difference is that, since we have a greater volume of water (charge), our “battery” will last longer.
Nuggets of Knowledge and Tidbits of Trivia
The International System of Units (SI) -- where SI is an abbreviation of Système International in French -- is the modern form of the metric system.
The SI symbol we use for “volt” (electrical potential) is ‘V,’ where the term volt itself is named after the Italian physicist Count Alessandro Giuseppe Antonio Anastasio Volta (1745–1827), who invented the electric battery in 1800.
We use the uppercase Greek letter Omega ‘Ω’ as the symbol of resistance, which is measured in units of ohms. When we say “ohm,” it sounds like “Oh” and “mmm” crunched together, which explains why we use ‘Ω’ as the symbol (sound them out: “ohm” and “Omega”). The term ohm is named after the German physicist Georg Simon Ohm, who we met earlier.
In an electrical circuit, we measure current in units of amps, where the term amp is named after the French mathematician and physicist André-Marie Ampère (1775–1836), who formulated one of the basic laws of electromagnetism in 1820. Somewhat confusingly, the SI symbol we use for current is the letter ‘I’, which originates from the French phrase intensité du courant, meaning “current intensity.”
As with all SI units whose names are derived from the proper name of a person, the first letter of its symbol is uppercase (e.g., ‘V’ and ‘I’). However, when the unit is spelled out, it should always be written in lowercase (e.g., “volt,” “amp,” “ohm”), unless it begins a sentence.
When we write things down, we can use the symbol (e.g., 5 V or 2 A) or the name (e.g., 5 volts or 2 amps), always with a space between the number and the qualifier; in conversation, we’d say “five volts” or “two amps.”
 max
max
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
I love how easy this article makes remembering all of that stuff. I also quite like the explanation on how to write and pronounce things.
One minor thing: I believe Volta's second to last name is spelled Anastasio (without a second 't').
Are you sure? yes | no
Eeek -- you are correct -- good catch -- I just went into the column and fixed it -- thanks for taking the time to point this out -- Max
Are you sure? yes | no
"while resistance (R) does its best to impede things"
I see what you did there. :D
Are you sure? yes | no
LOL :-)
Are you sure? yes | no
How cool! the 3rd drawing is the best ever :)
Are you sure? yes | no
LOL Whenever you create a series of columns like this, there's always a question as to what image style to use. I usually create 2D drawings in Visio -- and I may well do so in future columns -- but for the purposes of these columns I decided that hand-drawn images would be less "threatening" to beginners :-)
Are you sure? yes | no